Denge noktas civarnda dinamik sistemin davran iin kararllna

Denge noktası civarında dinamik sistemin davranışı için kararlılığına bakılır: Kaç tane denge noktası olabilir? Sistemin davranışını incelemenin bir yolu kararlılığını incelemektir. Tanım: Lyapunov anlamında kararlılık sistemine ilişkin bir denge noktası olsun. Verilen herhangi bir için Eşitsizliği eşitsizliğini gerektirecek şekilde bir bulunabiliyorsa noktası Lyapunov anlamında kararlıdır. Lineer sistemlerde denge noktasının Lyapunov anlamında kararlılığını incelemek için ne yapılıyor? Denge noktasının kararlılığı neye denk, neden? denge

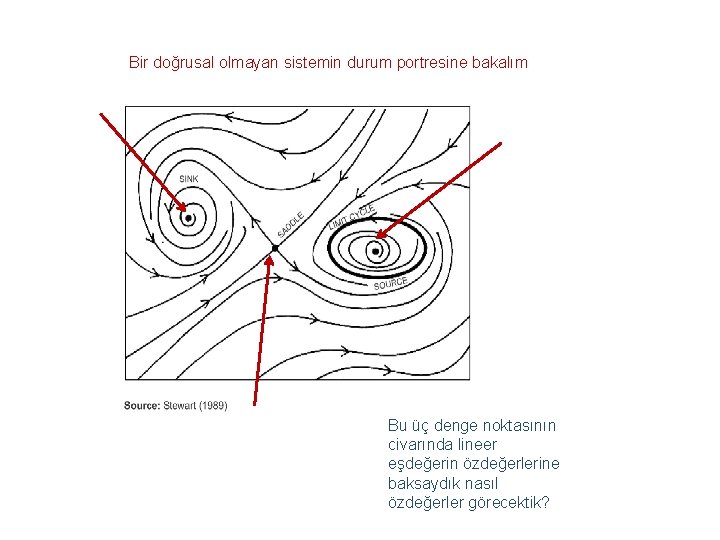
Bir doğrusal olmayan sistemin durum portresine bakalım Bu üç denge noktasının civarında lineer eşdeğerin özdeğerlerine baksaydık nasıl özdeğerler görecektik?

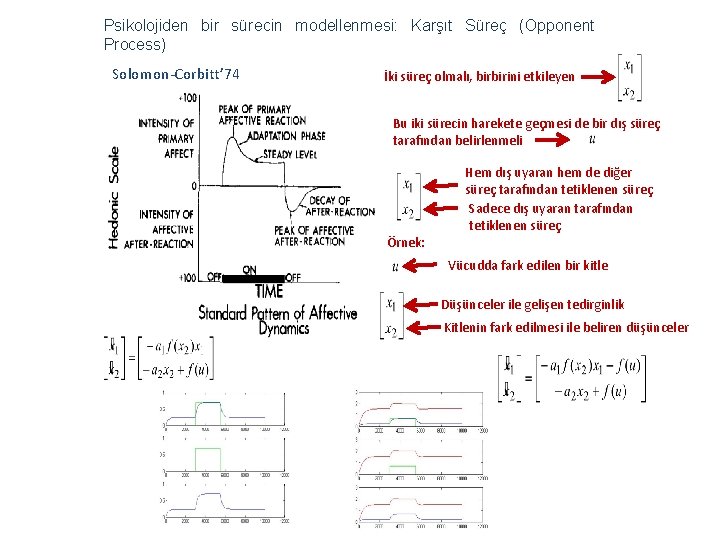
Psikolojiden bir sürecin modellenmesi: Karşıt Süreç (Opponent Process) Solomon-Corbitt’ 74 İki süreç olmalı, birbirini etkileyen Bu iki sürecin harekete geçmesi de bir dış süreç tarafından belirlenmeli Hem dış uyaran hem de diğer süreç tarafından tetiklenen süreç Sadece dış uyaran tarafından tetiklenen süreç Örnek: Vücudda fark edilen bir kitle Düşünceler ile gelişen tedirginlik Kitlenin fark edilmesi ile beliren düşünceler

Solomon-Corb, tt’ 74 makalesi sf. 126 - 129 Modelin açıklandığı bölümden yola çıkarak matematiksel modeli ve algoritmayı oluşturalım The primary a process for a given hedonic state is aroused by its adequate stimulus. We then imagine a single opponent loop generating the secondary b process and having an hedonic sign opposite to that of the state aroused by the input. The loop generating the b process is activated whenever any input evokes a sufficient hedonic consequence. The b process is sluggish, so it has a relatively long latency, recruits slowly, and dies out slowly. The affective system in Figure 3 receives a square wave input, and follows it with a dynamic affective response of the standard pattern The affective system in Panel A is shown as a single stage. Now, we will open the "black box" for this stage and look inside. Our proposal for the mechanism responsible for affective dynamics is shown in Figure 3, Panel B. Here, the affective stage is analyzed into its three component parts. The cognitive-perceptual stage has acted as a categorical detector. The informational signal enters the affective system as input to the first component, the a process, which has a short time constant. The signal from the a process activates the second component or b process, which responds with a slow rise and a slow decay. The third component is a summing device that adds the a and b signals, and it generates as its output the affective signal, which shows the sequence of the peak primary reaction A, adaptation, steady level, after-reaction B, and decay of B.

Thus, we see that the input from the perceptual cognitive stage has an affective, hedonic side effect, Process a. When it does, the opponent loop is activated, calling into play the opponent process (which has a hedonic quality in some way opposite to, and very different from, that of Process a). The opponent process, which we call Process b, reduces the hedonic intensity of the state which the input initially aroused. When the perceptual-cognitive input ceases, the opponent process reveals itself as "pure « State B, because the b process takes a while to decay. The block diagram of the affect-control system in Figure 3 yields the temporal dynamics of affect shown in Figure 4, Panel A. There we first see a baseline state. Then the affect-arousing stimulus is presented and it stays on for 10 seconds. Next, it is suddenly terminated. This simple event sequence activates the underlying opponent processes. First, there is a quick rise of Process a to a peak intensity. Shortly afterward, there is a slow recruitment of Process b. When the stimulus is terminated, Process a quickly goes to zero, but Process b, having a sluggish decay property, perseverates and dies out slowly. The resultant manifest dynamics of affect are a consequence of subtracting the b process from the a process. We postulated that the /; process is a slave process. That means that at first it cannot be aroused directly by ordinary sensory inputs, but instead can arise only indirectly via the arousal of an a process (see Figure 3) and the subsequent activation of the opponent loop. Şimdi bu haliyle anladığımızı hem denklemler ile ifade etmeye hem de algoritmayı oluşturmaya çalışalım.

a 1=0. 5 %%%%%%opponent_process için bir model%%%%%Kasım 7, 2016%%%%%%%amaç: opponent process için bir model oluşturmak%%% a 1=1 clear all; %%%%sistem 1%%% x 1=0; a 1=0. 5; theta 1=0. 2; %%%%sistem 2%%% x 2=0; a 2=0. 5; theta 2=1; %%%sayısal hesap için gerekenler%%% iterasyon=10000; mu=0. 01; %%% for k=1: iterasyon if k<3000|k>5500 u(k)=0; else u(k)=0. 7; end x 1(k+1)=x 1(k)+mu*(a 1*F_opponent(x 2(k), theta 1)*x 1(k)+F_opponent(u(k), theta 1)*(1 -x 1(k)*x 2(k))); x 2(k+1)=x 2(k)+mu*(-a 2*x 2(k)+F_opponent(u(k), theta 2)*(1 -x 2(k))); end subplot(3, 1, 1), plot(x 1, 'r'), hold on, plot(x 2), hold on, plot(u, 'g') subplot(3, 1, 2), plot(x 1, 'r'), hold on, plot(u, 'g') subplot(3, 1, 3), plot(x 1, 'r'), hold on, plot(x 2)

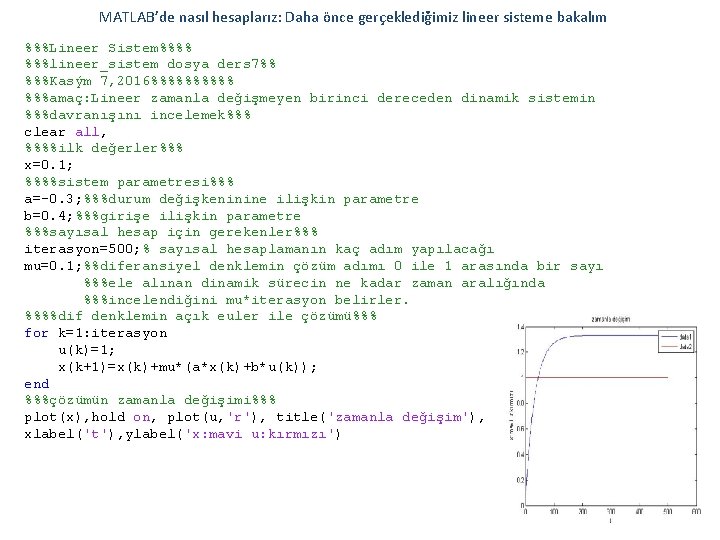
MATLAB’de nasıl hesaplarız: Daha önce gerçeklediğimiz lineer sisteme bakalım %%%Lineer Sistem%%%% %%%lineer_sistem dosya ders 7%% %%%Kasým 7, 2016%%%%% %%%amaç: Lineer zamanla değişmeyen birinci dereceden dinamik sistemin %%%davranışını incelemek%%% clear all, %%%%ilk değerler%%% x=0. 1; %%%%sistem parametresi%%% a=-0. 3; %%%durum değişkeninine ilişkin parametre b=0. 4; %%%girişe ilişkin parametre %%%sayısal hesap için gerekenler%%% iterasyon=500; % sayısal hesaplamanın kaç adım yapılacağı mu=0. 1; %%diferansiyel denklemin çözüm adımı 0 ile 1 arasında bir sayı %%%ele alınan dinamik sürecin ne kadar zaman aralığında %%%incelendiğini mu*iterasyon belirler. %%%%dif denklemin açık euler ile çözümü%%% for k=1: iterasyon u(k)=1; x(k+1)=x(k)+mu*(a*x(k)+b*u(k)); end %%%çözümün zamanla değişimi%%% plot(x), hold on, plot(u, 'r'), title('zamanla değişim'), xlabel('t'), ylabel('x: mavi u: kırmızı')

Girişde biraz değişiklik yapalım: %%%Lineer Sistem%%%% %%%lineer_sistem_giris_2 dosya ders 7%% %%%Kasým 7, 2016%%%%% %%%amaç: Lineer zamanla değişmeyen birinci dereceden dinamik sistemin %%%davranışını incelemek%%% clear all, %%%%ilk değerler%%% x=0. 1; %%%%sistem parametresi%%% a=-0. 3; %%%durum değişkeninine ilişkin parametre b=0. 4; %%%girişe ilişkin parametre %%%sayısal hesap için gerekenler%%% iterasyon=500; % sayısal hesaplamanın kaç adım yapılacağı mu=0. 1; %%diferansiyel denklemin çözüm adımı 0 ile 1 arasında bir sayı %%%ele alınan dinamik sürecin ne kadar zaman aralığında %%%incelendiğini mu*iterasyon belirler. %%%%dif denklemin açık euler ile çözümü%%% for k=1: iterasyon if k<100|k>150 u(k)=0; else u(k)=1; end x(k+1)=x(k)+mu*(a*x(k)+b*u(k)); end %%%çözümün zamanla değişimi%%% plot(x), hold on, plot(u, 'r'), title('zamanla değişim'), xlabel('t'), ylabel('x: mavi u: kırmızı')

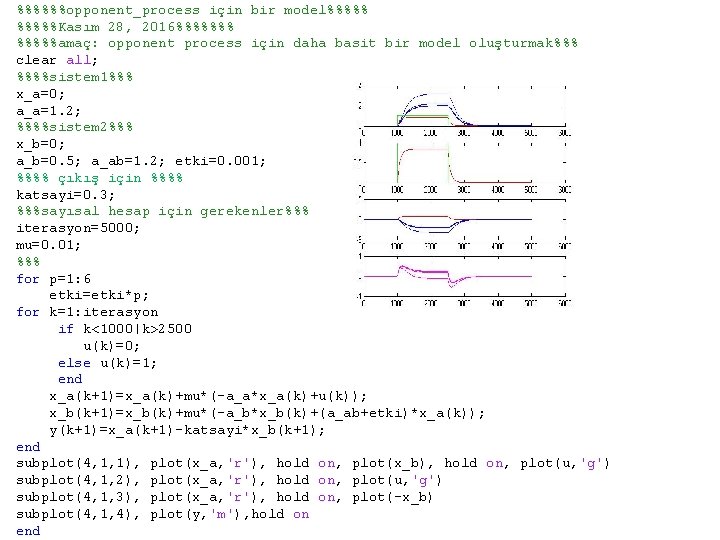
%%%%%%opponent_process için bir model%%%%%Kasım 28, 2016%%%%%%%amaç: opponent process için daha basit bir model oluşturmak%%% clear all; %%%%sistem 1%%% x_a=0; a_a=1. 2; %%%%sistem 2%%% x_b=0; a_b=0. 5; a_ab=1. 2; %%%% çıkış için %%%% katsayi=0. 3; %%%sayısal hesap için gerekenler%%% iterasyon=5000; mu=0. 01; %%% for k=1: iterasyon if k<1000|k>2500 u(k)=0; else u(k)=1; end x_a(k+1)=x_a(k)+mu*(-a_a*x_a(k)+u(k)); x_b(k+1)=x_b(k)+mu*(-a_b*x_b(k)+a_ab*x_a(k)); y(k+1)=x_a(k+1)-katsayi*x_b(k+1); end subplot(4, 1, 1), plot(x_a, 'r'), hold on, plot(x_b), hold on, plot(u, 'g') subplot(4, 1, 2), plot(x_a, 'r'), hold on, plot(u, 'g') subplot(4, 1, 3), plot(x_a, 'r'), hold on, plot(-x_b) subplot(4, 1, 4), plot(y, 'm'),

%%%%%%opponent_process için bir model%%%%%Kasım 28, 2016%%%%%%%amaç: opponent process için daha basit bir model oluşturmak%%% clear all; %%%%sistem 1%%% x_a=0; a_a=1. 2; %%%%sistem 2%%% x_b=0; a_b=0. 5; a_ab=1. 2; etki=0. 001; %%%% çıkış için %%%% katsayi=0. 3; %%%sayısal hesap için gerekenler%%% iterasyon=5000; mu=0. 01; %%% for p=1: 6 etki=etki*p; for k=1: iterasyon if k<1000|k>2500 u(k)=0; else u(k)=1; end x_a(k+1)=x_a(k)+mu*(-a_a*x_a(k)+u(k)); x_b(k+1)=x_b(k)+mu*(-a_b*x_b(k)+(a_ab+etki)*x_a(k)); y(k+1)=x_a(k+1)-katsayi*x_b(k+1); end subplot(4, 1, 1), plot(x_a, 'r'), hold on, plot(x_b), hold on, plot(u, 'g') subplot(4, 1, 2), plot(x_a, 'r'), hold on, plot(u, 'g') subplot(4, 1, 3), plot(x_a, 'r'), hold on, plot(-x_b) subplot(4, 1, 4), plot(y, 'm'), hold on end