Decision Procedures in First Order Logic Decision Procedures

Decision Procedures in First Order Logic Decision Procedures for Equality Logic Daniel Kroening and Ofer Strichman 1

Part III – Decision Procedures for Equality Logic and Uninterpreted Functions n Algorithm I – From Equality to Propositional Logic ¨ Adding transitivity constraints ¨ Making the graph chordal ¨ An improved procedure: consider polarity n Algorithm II – Range-Allocation ¨ What is the small-model property? ¨ Finding a small adequate range (domain) to each variable ¨ Reducing to Propositional Logic Decision Procedures An algorithmic point of view 2

Decision Procedures for Equality Logic n We will first investigate methods that solve Equality Logic. Uninterpreted functions are eliminated with one of the reduction schemes. n Our starting point: the E-Graph GE( E) n Recall: GE( E) represents an abstraction of E: It represents ALL equality formulas with the same set of equality predicates as E Decision Procedures An algorithmic point of view 3

From Equality to Propositional Logic Bryant & Velev 2000: the Sparse method = x 1 = x 2 Æ x 2 = x 3 Æ x 1 x 3 enc = e 1 Æ e 2 Æ : e 3 e 2 e 3 E e 1 n Encode all edges with Boolean variables ¨ (note: for now, ignore polarity) ¨ This is an abstraction ¨ Transitivity of equality is lost! ¨ Must add transitivity constraints! Decision Procedures An algorithmic point of view 4

From Equality to Propositional Logic E = x 1 = x 2 Æ x 2 = x 3 Æ x 1 x 3 e 2 Æ : e 3 enc = e 1 Æ e 2 e 1 n For each cycle add a transitivity constraint trans = (e 1 Æ e 2 ! e 3) Æ (e 1 Æ e 3 ! e 2) Æ (e 3 Æ e 2 ! e 1) Check: enc Æ trans Decision Procedures An algorithmic point of view 5

From Equality to Propositional Logic n There can be an exponential number of cycles, so let’s try to make it better. n Thm: it is sufficient to constrain simple cycles only T e 2 T T e 3 e 4 F e 1 e 6 T e 5 T Decision Procedures An algorithmic point of view 6

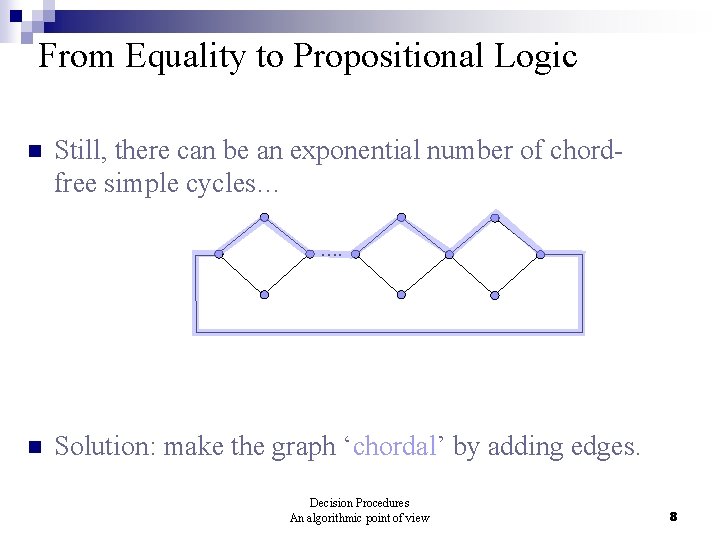
From Equality to Propositional Logic n Still, there is an exponential number of simple cycles. n Thm [Bryant & Velev]: It is sufficient to constrain chord-free simple cycles T e 2 T F e 1 e 5 F T e 3 T e 4 Decision Procedures An algorithmic point of view 7

From Equality to Propositional Logic n Still, there can be an exponential number of chordfree simple cycles… …. n Solution: make the graph ‘chordal’ by adding edges. Decision Procedures An algorithmic point of view 8

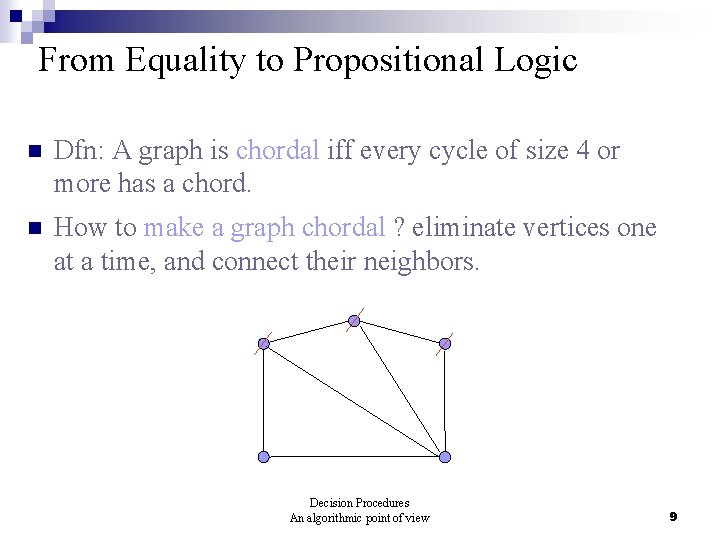
From Equality to Propositional Logic n Dfn: A graph is chordal iff every cycle of size 4 or more has a chord. n How to make a graph chordal ? eliminate vertices one at a time, and connect their neighbors. Decision Procedures An algorithmic point of view 9

From Equality to Propositional Logic n Once the graph is chordal, we can constrain only the triangles. T T Contradiction! T T F T T n Note that this procedure adds not more than a polynomial # of edges, and results in a polynomial no. of constraints. Decision Procedures An algorithmic point of view 10

Improvement n So far we did not consider the polarity of the edges. n Claim: in the following graph trans = e 3 Æ e 2 ! e 1 is sufficient e 1 e 3 e 2 n This is only true because of monotonicity of NNF Decision Procedures An algorithmic point of view 11

Definitions n Dfn: A contradictory Cycle C is constrained under T if T does not allow this assignment T T C= T T F Decision Procedures An algorithmic point of view 12

Main theorem n If T R constrains all simple contradictory cycles, and S S S For every assignment , ² T ! ² T n R From the Sparse method then E is satisfiable iff B Æ T The Equality Formula S R is satisfiable Decision Procedures An algorithmic point of view 13

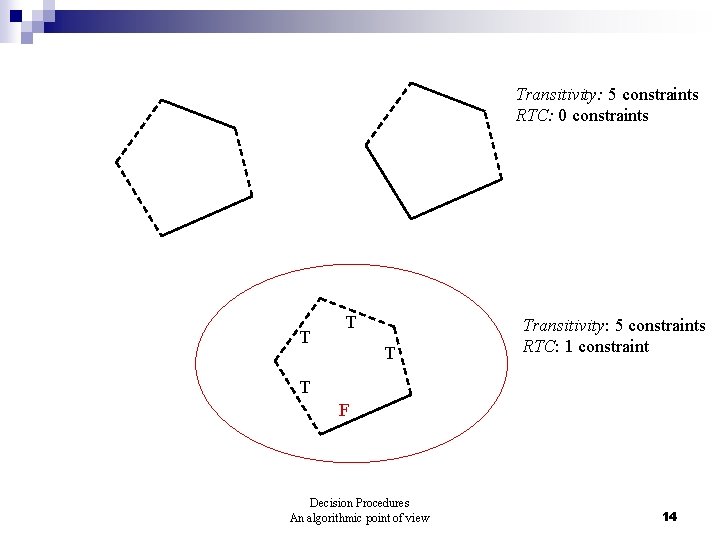
Transitivity: 5 constraints RTC: 0 constraints T Transitivity: 5 constraints RTC: 1 constraint T F Decision Procedures An algorithmic point of view 14

Proof of the main theorem n ( ) E is satisfiable BÆT S is satisfiable BÆT is satisfiable n ( ) Proof strategy: R R be a satisfying assignment to B Æ T R ¨ We will construct S that satisfies B Æ T S ¨ From this we will conclude that E is satisfiable ¨ Let Decision Procedures An algorithmic point of view Skip proof 15

Definitions for the proof… n A Violating cycle under an assignment R: F e. T 1 T Either dashed or solid T e. T 2 n This assignment violates T S but not necessarily T Decision Procedures An algorithmic point of view R 16

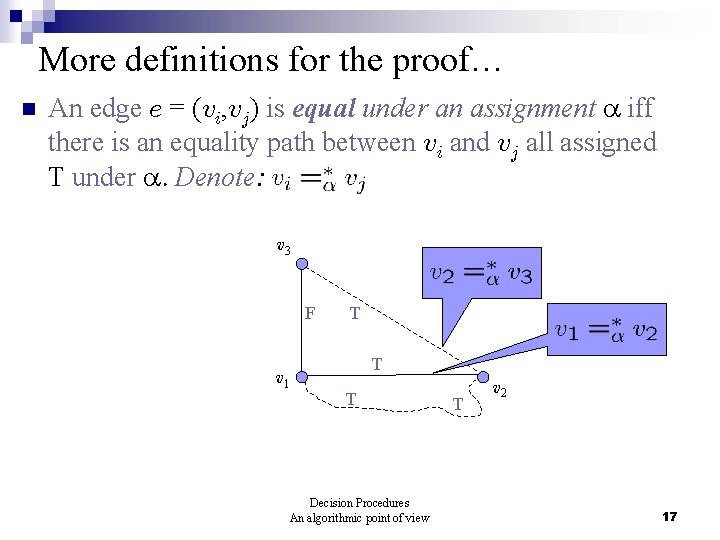
More definitions for the proof… n An edge e = (vi, vj) is equal under an assignment iff there is an equality path between vi and vj all assigned T under . Denote: v 3 F v 1 T T T Decision Procedures An algorithmic point of view T v 2 17

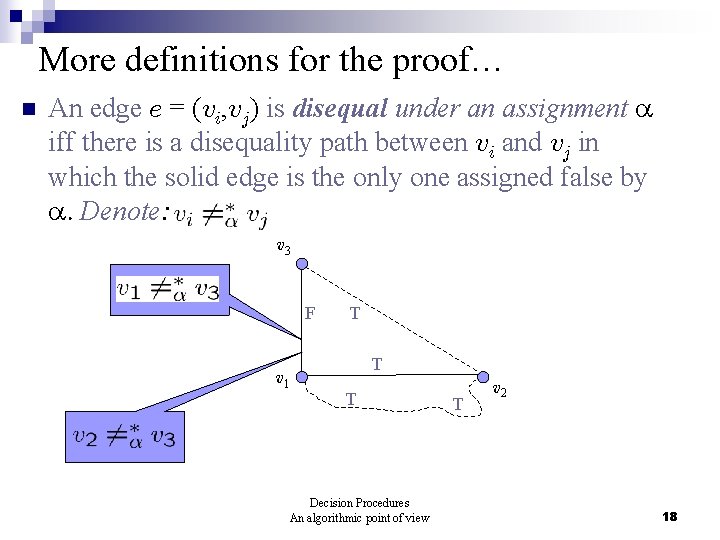
More definitions for the proof… n An edge e = (vi, vj) is disequal under an assignment iff there is a disequality path between vi and vj in which the solid edge is the only one assigned false by . Denote: v 3 F v 1 T T T Decision Procedures An algorithmic point of view T v 2 18

Proof… n Observation 1: The combination is impossible if = R (recall: R ² T R) v 3 F T T v 1 n v 2 Observation 2: if (v 1, v 3) is solid, then Decision Procedures An algorithmic point of view 19

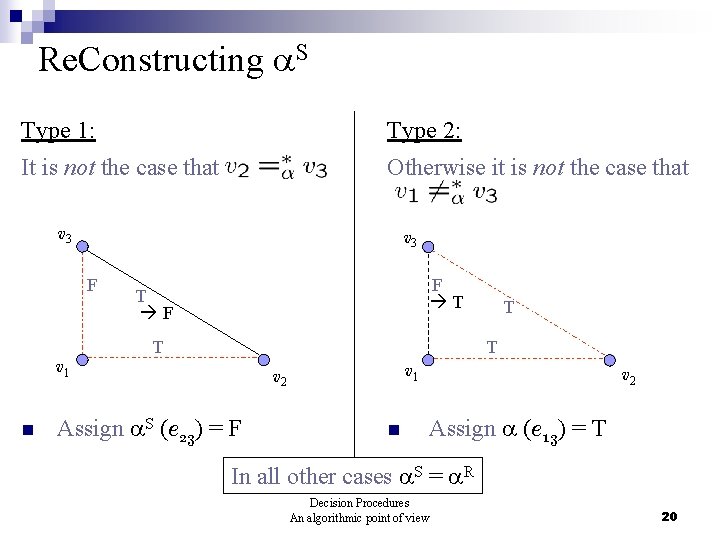
Re. Constructing S Type 1: Type 2: It is not the case that Otherwise it is not the case that v 3 F F T T v 1 n T v 1 v 2 Assign S (e 23) = F n v 2 Assign (e 13) = T In all other cases S = R Decision Procedures An algorithmic point of view 20

Re. Constructing S n Starting from R, repeat until convergence: (e. T) : = F in all Type 1 cycles ¨ (e. F) : = T in all Type 2 cycles ¨ n All Type 1 and Type 2 triangles now satisfy T n B is still satisfied (monotonicity of NNF) n Left to prove: all contradictory cycles are still satisfied Decision Procedures An algorithmic point of view S 21

Proof… n Invariant: contradictory cycles are not violating throughout the reconstruction. T v 3 F T T v 1 n v 2 contradicts the precondition to make this assignment… Decision Procedures An algorithmic point of view 22

Proof… n Invariant: contradictory cycles are not violating throughout the reconstruction. v 3 F T T F v 1 n v 2 contradicts the precondition to make this assignment… Decision Procedures An algorithmic point of view 23

Applying RTC n How can we use theorem without enumerating contradictory cycles ? n Answer: ¨ Consider the chordal graph. ¨ Constrain triangles if they are part of a (simple) contradictory cycle ¨ How? Decision Procedures An algorithmic point of view 24

• Should we constrain this triangle? • In which direction ? • Is this constraint necessary ? Decision Procedures An algorithmic point of view 26

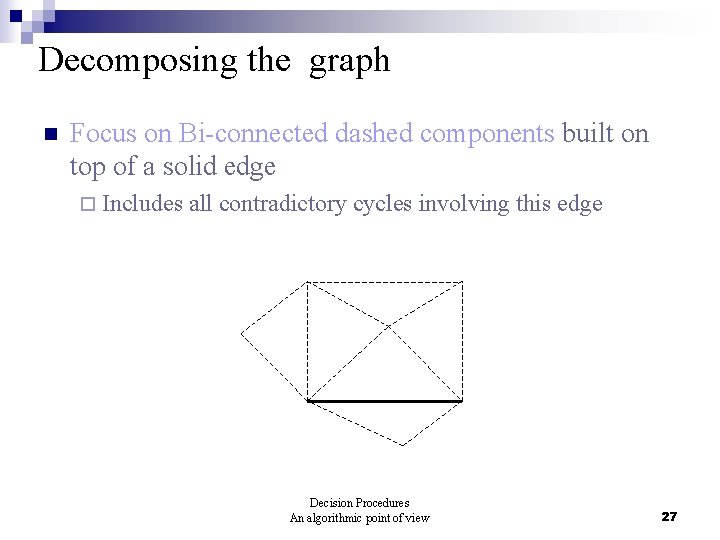
Decomposing the graph n Focus on Bi-connected dashed components built on top of a solid edge ¨ Includes all contradictory cycles involving this edge Decision Procedures An algorithmic point of view 27

n Make the component chordal ¨ Chordal-ity guarantees: every cycle contains a simplicial vertex, i. e. a vertex that its neighbors are connected. Decision Procedures An algorithmic point of view 28

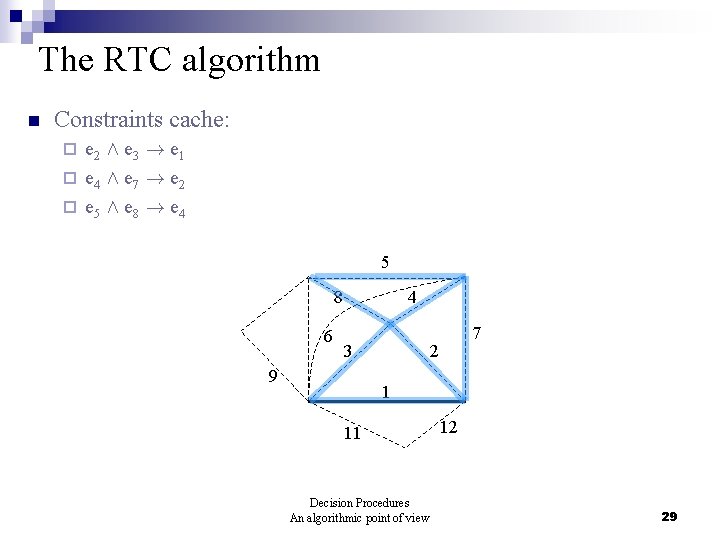
The RTC algorithm n Constraints cache: e 2 Æ e 3 ! e 1 ¨ e 4 Æ e 7 ! e 2 ¨ e 5 Æ e 8 ! e 4 ¨ 5 8 6 4 3 9 7 2 1 11 Decision Procedures An algorithmic point of view 12 29

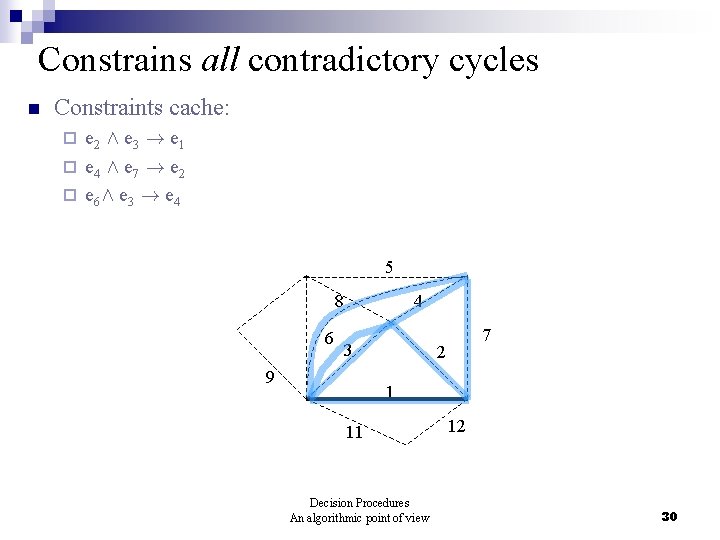
Constrains all contradictory cycles n Constraints cache: e 2 Æ e 3 ! e 1 ¨ e 4 Æ e 7 ! e 2 ¨ e 6 Æ e 3 ! e 4 ¨ 5 8 6 4 3 9 7 2 1 11 Decision Procedures An algorithmic point of view 12 30

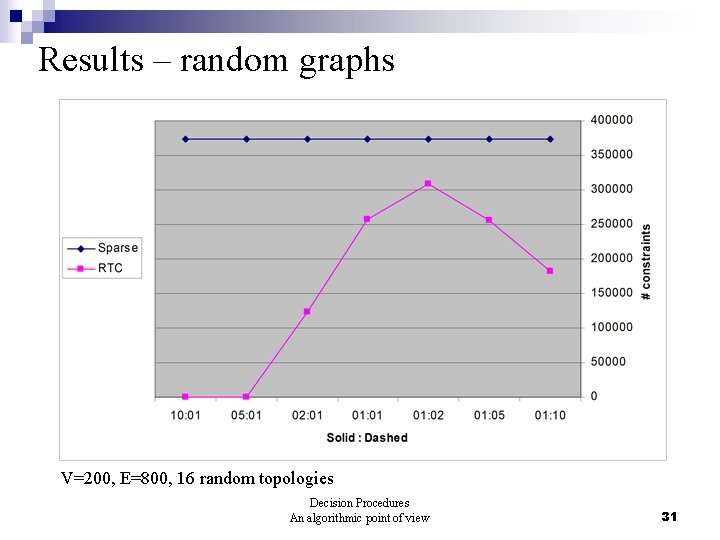
Results – random graphs V=200, E=800, 16 random topologies Decision Procedures An algorithmic point of view 31

Random graphs (Satisfiable) Decision Procedures An algorithmic point of view 32