Data Structures and Algorithms PLSD 210ii Searching Searching

Data Structures and Algorithms PLSD 210(ii) Searching

Searching • Sequential Searches • Time is proportional to n • We call this time complexity O(n) • Pronounce this “big oh” of n • Both arrays (unsorted) and linked lists • Binary search • Sorted array • Time proportional to log 2 n • Time complexity O(log n)

Searching - Binary search • Creating the sorted array • Add. To. Collection • adds each item in correct place c 1 log 2 n • Shuffle down c 2 n • Overall c 1 log 2 n + c 2 n Dominant or c 2 n term • Each add to the sorted array is O(n) ? Can we maintain a sorted array with cheaper insertions? • Find position

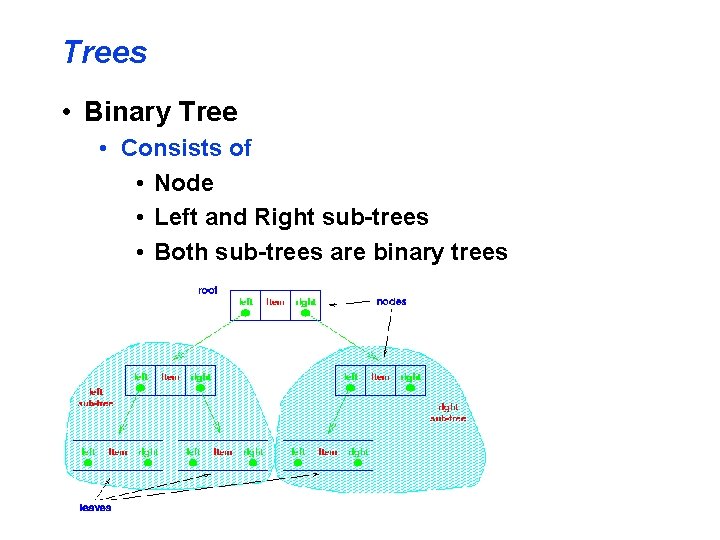
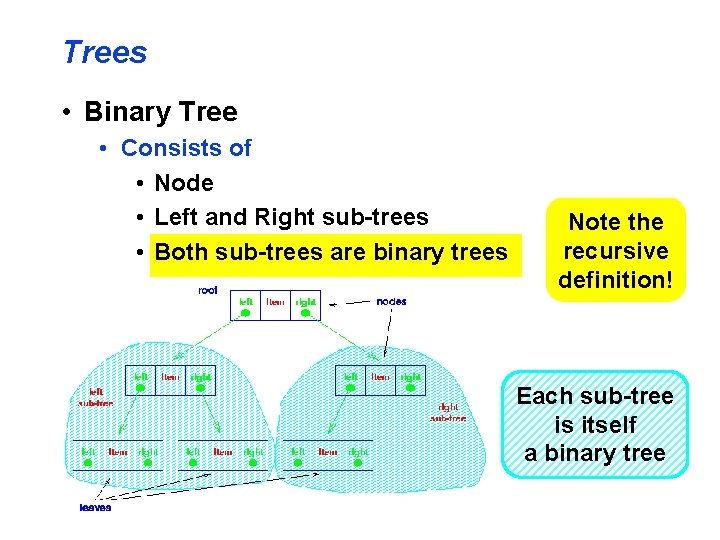
Trees • Binary Tree • Consists of • Node • Left and Right sub-trees • Both sub-trees are binary trees

Trees • Binary Tree • Consists of • Node • Left and Right sub-trees • Both sub-trees are binary trees Note the recursive definition! Each sub-tree is itself a binary tree

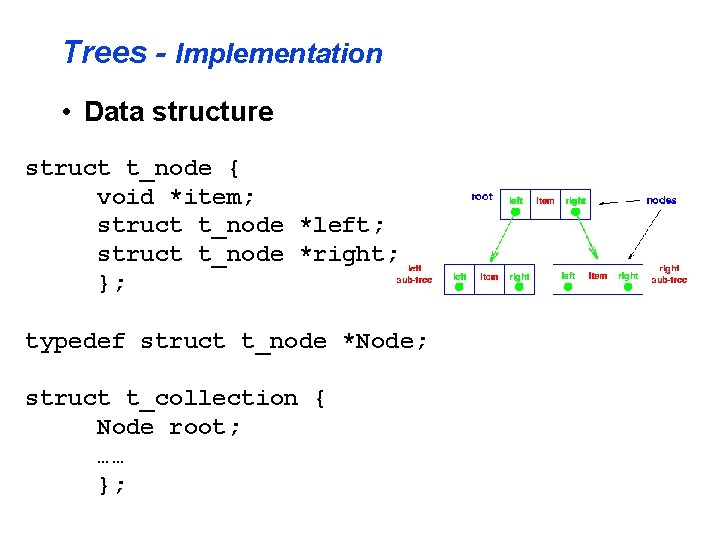
Trees - Implementation • Data structure struct t_node { void *item; struct t_node *left; struct t_node *right; }; typedef struct t_node *Node; struct t_collection { Node root; …… };

Trees - Implementation • Find extern int Key. Cmp( void *a, void *b ); /* Returns -1, 0, 1 for a < b, a == b, a > b */ void *Find. In. Tree( Node t, void *key ) { Less, if ( t == (Node)0 ) return NULL; search switch( Key. Cmp( key, Item. Key(t->item) ) ) { left case -1 : return Find. In. Tree( t->left, key ); case 0: return t->item; case +1 : return Find. In. Tree( t->right, key ); } Greater, } search right void *Find. In. Collection( collection c, void *key ) { return Find. In. Tree( c->root, key ); }

Trees - Implementation • Find • key = 22; if ( Find. In. Collection( c , &key ) ) …. n = c->root; Find. In. Tree( n, &key ); Find. In. Tree(n->right, &key ); Find. In. Tree(n->left, &key ); return n->item;

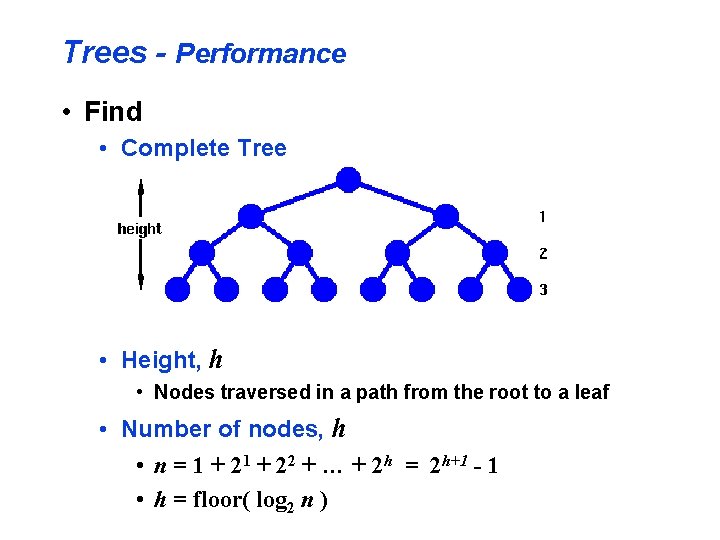
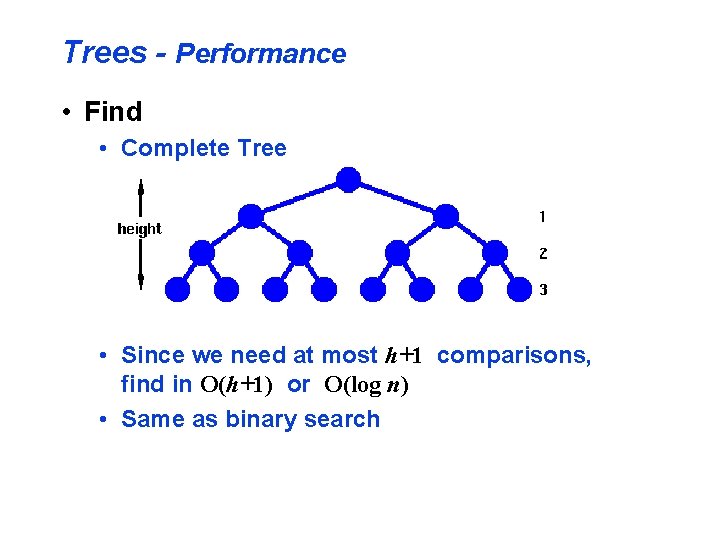
Trees - Performance • Find • Complete Tree • Height, h • Nodes traversed in a path from the root to a leaf • Number of nodes, h • n = 1 + 22 + … + 2 h = 2 h+1 - 1 • h = floor( log 2 n )

Trees - Performance • Find • Complete Tree • Since we need at most h+1 comparisons, find in O(h+1) or O(log n) • Same as binary search

Lecture 2 & 3 - Summary Add Delete Find Arrays Linked List Trees Simple, fast Inflexible O(1) O(n) inc sort O(n) Simple Flexible O(1) sort -> no adv O(1) - any O(n) - specific O(n) (no bin search) Still Simple Flexible O(n) O(logn) binary search O(log n)

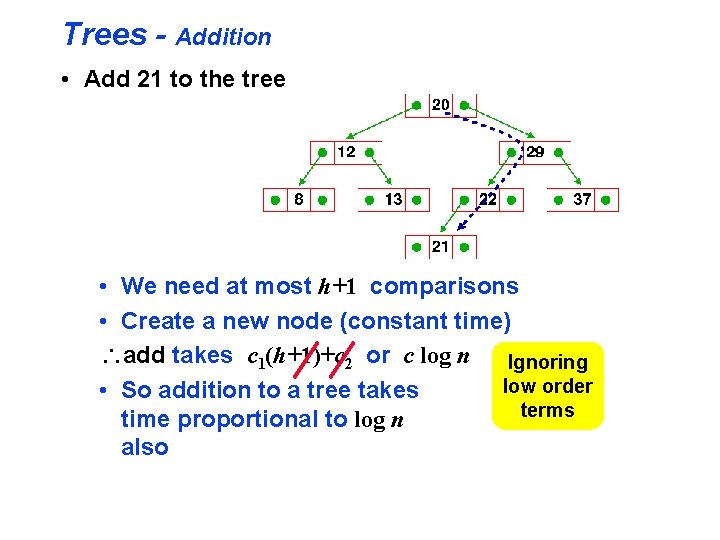
Trees - Addition • Add 21 to the tree • We need at most h+1 comparisons • Create a new node (constant time) add takes c 1(h+1)+c 2 or c log n Ignoring low order • So addition to a tree takes terms time proportional to log n also

Trees - Addition - implementation static void Add. To. Tree( Node *t, Node new ) { Node base = *t; /* If it's a null tree, just add it here */ if ( base == NULL ) { *t = new; return; } else if( Key. Less(Item. Key(new->item), Item. Key(base->item)) ) Add. To. Tree( &(base->left), new ); else Add. To. Tree( &(base->right), new ); } void Add. To. Collection( collection c, void *item ) { Node new, node_p; new = (Node)malloc(sizeof(struct t_node)); /* Attach the item to the node */ new->item = item; new->left = new->right = (Node)0; Add. To. Tree( &(c->node), new ); }

Trees - Addition • Find • Add • Delete c log n • Apparently efficient in every respect! • But there’s a catch ………. .

Trees - Addition • Take this list of characters and form a tree A B C D E F • ? ?

Trees - Addition • Take this list of characters and form a tree A B C D E F • In this case ? Find ? Add ? Delete