Data Flow Analysis 4 15 411 Compiler Design

Data Flow Analysis 4 15 -411 Compiler Design Nov. 8, 2005

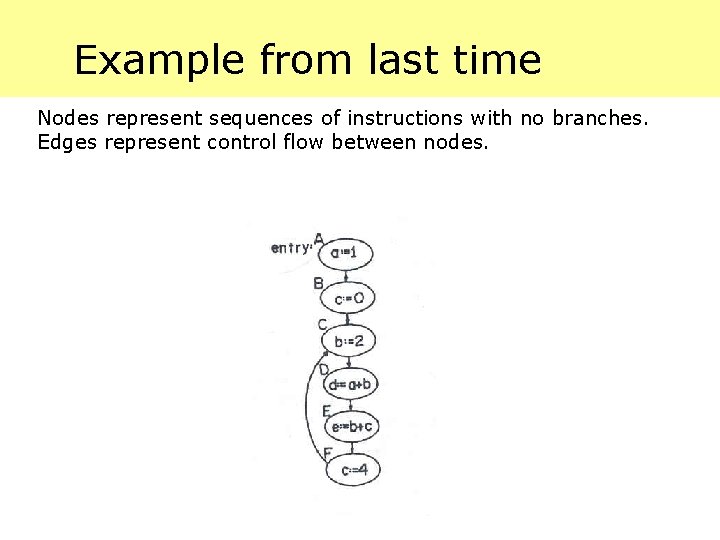
Example from last time Nodes represent sequences of instructions with no branches. Edges represent control flow between nodes.

Constant Propagation Convenient to associate a pool of propagated constants with each node in the graph. Pool is a set of ordered pairs which indicate variables that have constant values when node is encountered. The pool at node B denoted by PB consists of a single element (a, 1) since the assignment a: = 1 must occur before B.

Constant Pools Let V be a set of variables, C be a set of constants, and N be the set of nodes in the graph. The set U = V £ C represents ordered pairs which may appear in any constant pool. All constant pools are elements of the power set U, denoted P(U).

Constant Propagation (cont. ) Fundamental problem of constant propagation is to determine the pool of constants for each node in a program graph. By inspection of the program graph for the example, the pool of constants at each node is PA = PB = {(a, 1)} PC = {(a, 1)} PD = {(a, 1), (b, 2)} PE = {(a, 1), (b, 2), (d, 3)} PF = {(a, 1), (b, 2), (d, 3)}

Constant Propagation (cont. ) PN may be determined for each node N in the graph as follows: Consider each path (A, p 1, p 2, …, pn, N). Apply constant propagation along path to obtain set of constants at node N. Intersection for each path to N is the set of constants which can be assumed for optimization. (It is unknown what path will be taken at execution time, so intersection is conservative choice)

Constant Propagation (cont. ) Successively longer paths from A to D can be evaluated, resulting in PD, 3 , PD, 4 , …, PD, n for arbitrarily large n. The pool of constants that can be assumed no matter what flow of control occurs is the set of constants common to all PD, i , i. e. Åi PD, i This procedure is not effective since the number of such paths may have no finite bound, and the procedure would not halt.

Optimizing Function for Constant Propagation It is useful to define an optimizing function f which maps an input pool together with a particular node to a new output pool. The optimizing function for constant propagation is f: N £ P(U) ! P(U) where (v, c) 2 f(N, P) if and only if 1. (v, c) 2 P and the operation at node N does not assign a new value to the variable v. 2. The operation at N assigns an expression to the variable v, and the expression evaluates to the constant c.

Optimization Function for Example The optimizing function can be applied to node A with an empty constant pool resulting in f(A, ; ) = {(a, 1)}. The function can be applied to B with {(a, 1)} as the constant pool yielding f(B, {(a, 1)}) = {(a, 1), (c, 0)}.

Extending f to Paths in the Graph Given a path from entry node A to an arbitrary node N, optimizing pool for path is determined by composing the function f. For example, f(C, f(B, f(A, ; ))) = {(a, 1), (c, 0), (b, 2)} is the constant pool for D for this path. Sometimes the notation is cleaner to write f. C (f. B (f. A ( ))) or f. C ± f. B ± f. A ( ).

Computing the Pool of Optimizing Information. The pool of optimizing information which can be assumed at node N in the graph, independent of the path taken at execution time, is PN = Å {x | x 2 FN}. Here FN = { f(pn, f(pn-1, …, f(p 1, P))…)| (p 1, p 2, …, pn, N) is a path from an entry node p 1 with corresponding entry pool P to node N}.

Lattices • A partial order is a lattice if u and t are defined so that · u is the meet or greatest lower bound operation · x u y · x and x u y · If z · x and z · y then z · x u y · t is the join or least upper bound operation · x t y and y · x t y · If x · z and y · z, then x t y · z

Lattices (cont. ) A finite partial order is a lattice if meets and joins exist for every pair of elements A lattice has unique elements bot and top such that xu? =? x t ? =x xu>=x xt>=> In a lattice x · y iff x u y = x x · y iff x t y = y

Monotonicity A function f on a partial order is monotonic if and only if x · y implies f(x) · f(y) Can show that optimizing function f: N £ P(U) ! P(U) for constant propagation is monotonic in its second argument.

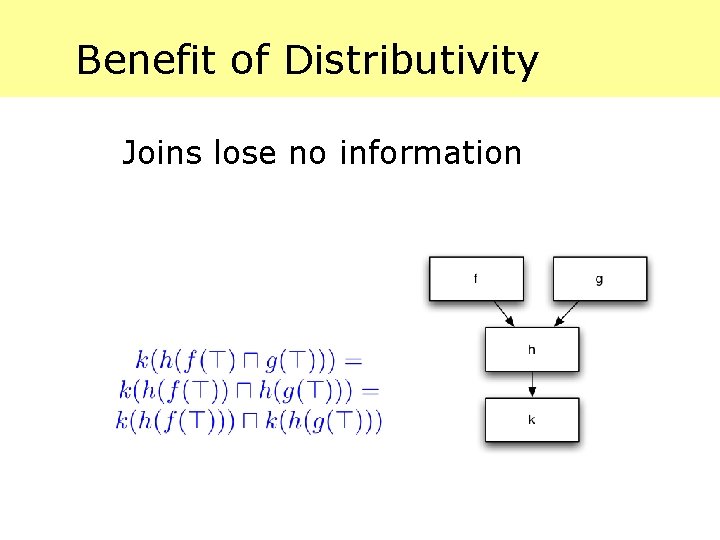
Distributive Data Flow Problems By monotonicity, we also have A function f is distributive or has the homomorphism property if

Benefit of Distributivity Joins lose no information

Accuracy of Data Flow Analysis Ideally, we would like to compute the meet over all paths (MOP) solution: · Let fi be the transfer function for statement si · If p is a path {s 1, . . . , sn}, let fp = fn± fn-1±. . . ± f 1 · Let path(s) be the set of paths from the entry to s If a data flow problem is distributive, then solving data flow equations in the standard way yields the MOP solution

What Problems are Distributive? Analyses of how the program computes · Live variables · Available expressions · Reaching definitions · Very busy expressions All Gen/Kill problems are distributive

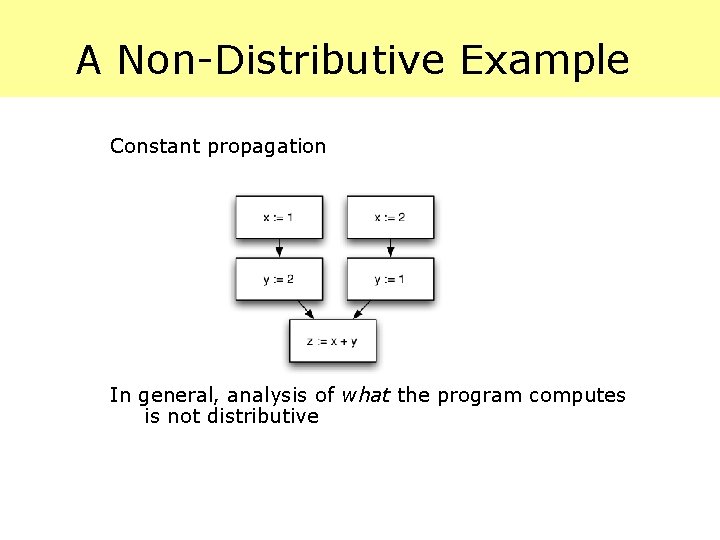
A Non-Distributive Example Constant propagation In general, analysis of what the program computes is not distributive

Constant Propagation and the Homomorphism Prop. Does the Optimizing function for Constant Propagation satisfy the homomorphism? F(1, ) = {(x, 1)} P 1= F(2, F(1, )) = {(x, 1), (y, 2)} F(3, P) = {(x, 2)) P 2 = F(4, F(3, )) = {(x, 2), (y, 1)} F(5, P 1 Å P 2) = F(5, ) = F(5, P 1)) = {(x, 1), (y, 2), (z, 3)} F(5, P 2)) = {(x, 2), (y, 1), (z, 3)} F(5, P 1) Å F(5, P 2) = {(z, 3)} = F(5, P 1 Å P 2)

Undecidability of MOP Problem Surprise!! The MOP problem is undecidable for Constant Propagation. No algorithm exists to compute the MOP solution for all instances of the constant propagation problem.

Meet-Semilatticies Let the finite set L be the set of all possible optimizing pools for a given application. Let u be a meet operation with the properties: u: L£L!L xuy=yux x u (y u z) = (x u y) u z where x, y z 2 L. The set L and the u operation define a finite meet-semilattice.

Ordering on Meet-Semilattices The u operation defines a partial ordering on L by x 6 y if and only if x u y = x. Similarly, x < y if and only if x 6 y and x y.

Monotone Data Flow Analysis Frameworks A monotone data flow analysis framework is a triple D= (L, u , F) where 1. (L, u) is a semilattice of finite length with zero element 0, and 2. F is a monotone operation space associate with L.

Monotone Operation Spaces Let (L, u) be a semilattice of finite length with a zero element. A set of operations F on L is said to be a monotone operation space associated with L iff the following conditions hold: 1. Each f 2 F is monotonic, i. e. , 2. (8 x, y 2 L)[x 6 y implies that f(x) 6 f(y)]. 2. There exists an identity operation e in F, i. e. (9 e 2 F) (8 x 2 L) [e(x) = x] 3. F is closed under composition, i. e. , (8 f, g 2 F)[f ± g 2 F] 4. For each x 2 F there exists an f 2 F such that x = f(0).

Distributive Frameworks A monotone framework D = (L, u, F) is called a distributive framework if and only if (8 f 2 F) (8 x, y 2 L) [f(x u y) = f(x) u f(y)]. This really just the homomorphism property mentioned earlier.

Maximum Fixpoint Solution (MFP) Let I = (G, M) be an instance of a monotone framework D = (L, u, F). Let fi(P) be the operation associated with node i, and let the nodes of G be numbered from 2 to n by r. Postorder. The maximum fixed point (MFP) solution of I is defined as the maximum fixed point of the following equations. x 1 = 0, xi =u j 2 pred(i) fj (xj) for 2 6 i 6 n.

Conditions for Algorithm u If X ½ L, the generalized meet operation X is defined as the pairwise application of u to the elements of X. L is assumed to have a “zero element” 0 such that 0 6 x for all x 2 L. An augmented set L’ is constructed from L by adding a “unit element” 1 such that 1 is not in L and 1 Æ x = x for all x in L. The set L’ = L [ {1}. It follows that x <1 for all x in L.

Conditions for Algorithm (cont. ) Need an “optimizing function” f: N £ L ! L. It should have the distributive or homomorphism property: F(N, x Æ y) = f(N, x) Æ f(N, y) for all N 2 N and x, y 2 L. Note that f(N, x) < 1 for all N 2 N and x 2 L.

Global Analysis Algorithm Global analysis starts with an entry pool set EP ½ I £ L, where (e, x) 2 EP if e 2 I is an entry node with optimizing pool x 2 L. A 1 [initialize] L : = EP. A 2 [terminate ? ] If L = ; then halt. A 3 [select node] Let L’ 2 L, L’ = (N, Pi) for some N 2 N and Pi 2 L. Then L : = L – {L’}. A 4 [Traverse] Let PN be the current approximate pool for node N (Initially PN = 1). If PN 6 Pi the go to step A 2. A 5 [set pool] PN : = PN Æ Pi, L: = L [ {(N’, f(N, PN)) | N’ 2 I(N)}. A 6 [Loop] Go to step A 2.

MOP vs. MFP Solutions Kildall provided a general iterative algorithm for distributive frameworks (see previous slide). He proved that his algorithm converges to the MFP solution of a distributive framework and that for distributive frameworks the MFP solution is equal to the MOP solution. Kam and Ullman proved that when Kildall’s iterative algorithm is applied to a monotone framework, it converges to the MFP solution of that framework.