Introduction to Data Flow Analysis 1 Data Flow

Introduction to Data Flow Analysis 1

Data Flow Analysis • Construct representations for the structure of flow-of-data of programs based on the structure of flow-of-control of programs • Collect information about the attributes of data at various program points according to the structure of flow-of-data of programs 2

Points • Within each basic block, a point is assigned between two adjacent statements, before the first statement, and after the last statement 3

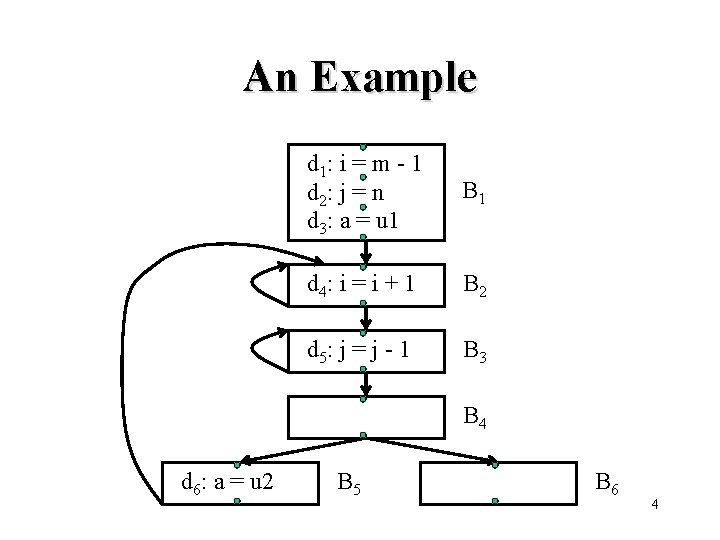
An Example d 1: i = m - 1 d 2: j = n d 3: a = u 1 B 1 d 4: i = i + 1 B 2 d 5: j = j - 1 B 3 B 4 d 6: a = u 2 B 5 B 6 4

Paths • A path from p 1 to pn is a sequence of points p 1, p 2, …, pn such that for each i, 1 i n-1, either • pi is the point immediately preceding a statement and pi+1 is the point immediately following that statement in the same block, or • pi is the end of some block and pi+1 is the beginning of a successor block 5

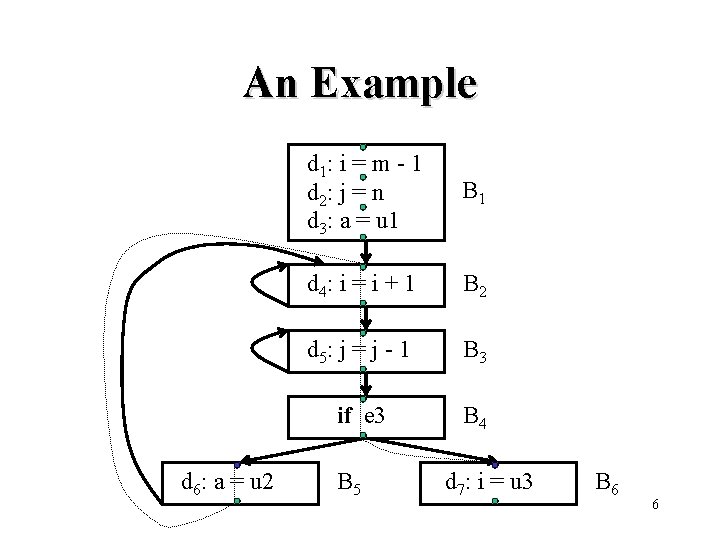
An Example d 6: a = u 2 d 1: i = m - 1 d 2: j = n d 3: a = u 1 B 1 d 4: i = i + 1 B 2 d 5: j = j - 1 B 3 if e 3 B 4 B 5 d 7: i = u 3 B 6 6

Reaching Definitions • A definition of a variable x is a statement that assigns or may assign a value to x • A definition d of some variable x reaches a point p if there is a path from the point immediately following d to p such that no unambiguous definition of x appear on that path 7

An Example d 1: i = m - 1; d 2: j = n; d 3: a = u 1; do d 4: i = i + 1; d 5: j = j - 1; if e 1 then d 6: a = u 2 else d 7: i = u 3 while e 2 8

Ambiguity of Definitions • Unambiguous definitions (must assign values) – assignments to a variable – statements that read a value to a variable • Ambiguous definitions (may assign values) – procedure calls that have call-by-reference parameters – procedure calls that may access nonlocal variables – assignments via pointers 9

Safe or Conservative Information • Consider all execution paths of the control flow graph • Allow definitions to pass through ambiguous definitions of the same variables • The computed set of reaching definitions is a superset of the exact set of reaching definitions 10

Information for Reaching Definitions • gen[S]: definitions generated within S and reaching the end of S • kill[S]: definitions killed within S • in[S]: definitions reaching the beginning of S • out[S]: definitions reaching the end of S 11

Data Flow Equations • Data flow information can be collected by setting up and solving systems of equations that relate information at various points out[S] = gen[S] (in[S] - kill[S]) The information at the end of a statement is either generated within the statement or enters at the beginning and is not killed as 12 control flows through the statement

The Iterative Algorithm • Repeatedly compute in and out sets for each node in the control flow graph simultaneously until there is no change in[B] = p pred(B) out[P] out[B] = gen[B] (in[B] - kill[B]) 13

Algorithm: Reaching Definitions /* Assume in[B] = for all B */ for each block B do out[B] : = gen[B] change : = true; while change do begin change : = false; for each block B do begin in[B] : = p pred(B) out[p] oldout : = out[B] : = gen[B] (in[B] - kill[B]) if out[B] oldout then change : = true end 14

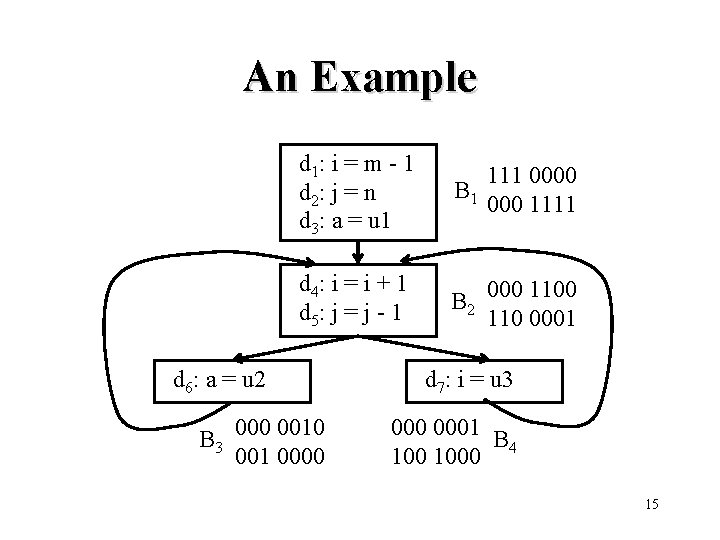
An Example d 1: i = m - 1 d 2: j = n d 3: a = u 1 111 0000 B 1 000 1111 d 4: i = i + 1 d 5: j = j - 1 B 2 000 110 0001 d 6: a = u 2 B 3 000 001 0000 d 7: i = u 3 0001 B 1000 4 15

An Example Block Initial In[B] Out[B] Pass 1 In[B] Out[B] Pass 2 In[B] Out[B] B 1 000 0000 111 0000 B 2 0000 000 111 001 1110 1111 001 1110 B 3 0000 0010 001 1110 000 1110 B 4 0000 0001 001 1110 001 0111 16

Conservative Computation • The computed gen set of reaching definitions is a superset of the exact gen set of reaching definitions • The computed kill set of reaching definitions is a subset of the exact kill set of reaching definitions • The computed in and out sets of reaching definitions is a superset of the exact in and out sets of reaching definitions 17

Local Data Flow Information • The gen and kill sets for a basic block is obtained from the gen and kill sets for the statements in the basic block • Only the in and out sets for the basic blocks are computed in the global data flow analysis • The in and out sets for the statements in a basic block can be computed locally from the in set for the basic block if necessary 18

UD-Chains and DU-Chains • A variable is used at statement s if its rvalue may be required • The reaching definitions information is often stored as use-definition chains (or udchains) • The ud-chain for a use u of a variable x is the list of all the definitions of x that reach u • The definition-use chains (or du-chains) for a definition d of a variable x is the list of all the uses of x that use the value defined at d 19

A Taxonomy of Data Flow Problems Forward-Flow Backward-Flow Any in[B] = p pred(B) out[p] out[B] = s succ(B) in[s] path out[B] = gen[B] (in[B] - kill[B]) in[B] = gen[B] (out[B] - kill[B]) All in[B] = p pred(B) out[p] path out[B] = gen[B] (in[B] - kill[B]) in[B] = gen[B] (out[B] - kill[B]) out[B] = s succ(B) in[s] 20

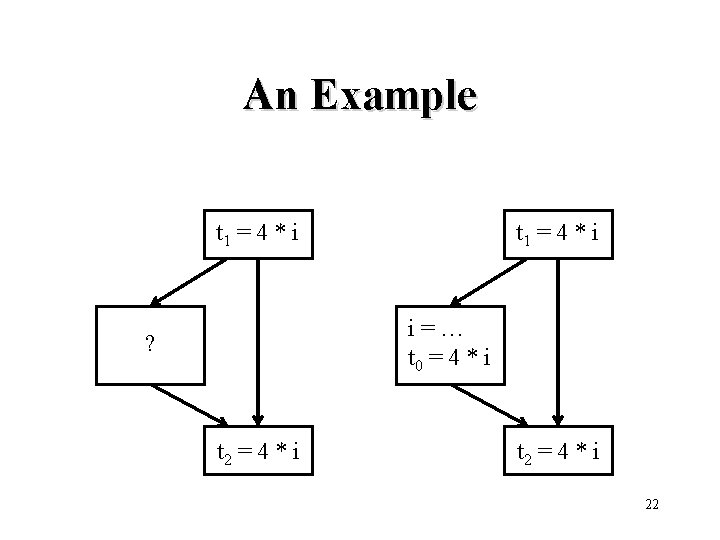
Available Expressions • An expression x+y is available at a point p if every path from the initial node to p evaluates x+y, and after the last such evaluation prior to reaching p, there are no subsequent assignments to x or y 21

An Example t 1 = 4 * i i=… t 0 = 4 * i ? t 2 = 4 * i 22

The gen and kill Sets • A block kills expression x+y if it possibly assign x or y and does not subsequently reevaluate x+y • A block generates expression x+y if it definitely evaluates x+y and does not subsequently redefine x or y 23

The gen Set for a Block • No expressions are available at the beginning • Assume set A of expressions is available before statement x = y+z. The set of expressions available after the statement is formed by – adding to A the expression y+z – deleting from A any expression involving x • At the end, A is the set of generated expressions 24

The kill Set for a Block • All expressions y+z such that either y or z is defined and y+z is not generated by the block 25

An Example Statements Available Expressions ………………none a=b+c ………………only b + c b=a-d ………………only a - d c=b+c ……………only a - d d=a-d ……………none 26

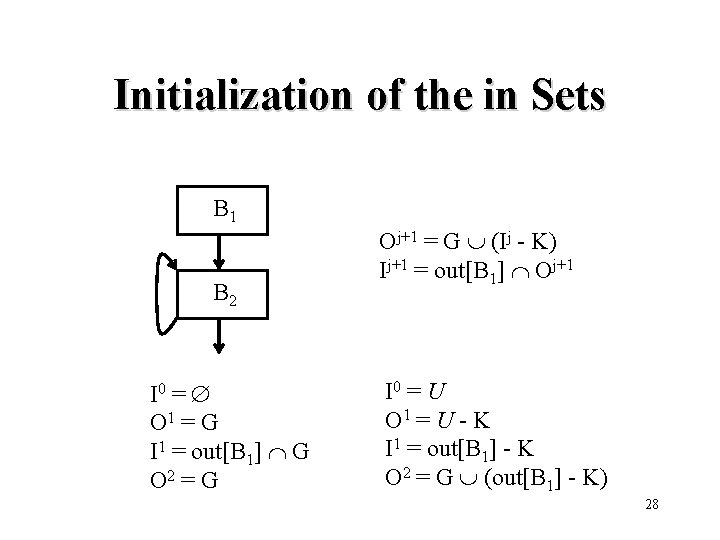
The in and out Sets in[B] = , for B = initial in[B] = p pred(B) out[p], for B initial out[B] = gen[B] (in[B] - kill[B]) 27

Initialization of the in Sets B 1 B 2 I 0 = O 1 = G I 1 = out[B 1] G O 2 = G Oj+1 = G (Ij - K) Ij+1 = out[B 1] Oj+1 I 0 = U O 1 = U - K I 1 = out[B 1] - K O 2 = G (out[B 1] - K) 28

Algorithm: Available Expressions /* Assume in[B 1] = and in[B] = U for all B B 1 */ in[B 1] = ; out[B 1] = gen[B 1]; for each block B B 1 do out[B] : = U - kill[B]; change : = true; while change do begin change : = false; for each block B B 1 do begin in[B] : = p pred(B) out[p] oldout : = out[B] : = gen[B] (in[B] - kill[B]) if out[B] oldout then change : = true end 29

Conservative Computation • The computed gen set of available expressions is a subset of the exact gen set of available expressions • The computed kill set of available expressions is a superset of the exact kill set of available expressions • The computed in and out sets of available expressions is a subset of the exact in and out sets of available expressions 30

Live Variables • A variable x is live at a point p if the value of x at p could be used along some path in the control flow graph starting at p; otherwise, x is dead at p 31

The def and use Sets • def[B]: the set of variables definitely assigned values in B • use[B]: the set of variables whose values are possibly used in B prior to any definition of the variable 32

The in and out Sets out[B] = s succ(B) in[s] in[B] = use[B] (out[B] - def[B]) 33

Algorithm: Live Variables /* Assume in[B] = for all B */ for each block B do in[B] : = change : = true; while change do begin change : = false; for each block B do begin out[B] : = s succ(B) in[s] oldin : = in[B] : = use[B] (out[B] - def[B]) if in[B] oldin then change : = true end 34

Conservative Computation • The computed use set of live variables is a superset of the exact use set of live variables • The computed def set of live variables is a subset of the exact def set of live variables • The computed in and out sets of live variables is a superset of the exact in and out sets of live variables 35

Busy Expressions • An expression is busy at a point p if along all paths from p to the final node its value is used before the expression is killed 36

The use and kill Sets • use[B]: the set of expressions that are used before they are killed in B • kill[B]: the set of expressions that are killed before they are used in B 37

The in and out Sets out[B] = , for B = final out[B] = s succ(B) in[s], for B final in[B] = use[B] (out[B] - kill[B]) 38

Algorithm: Busy Expressions /* Assume out[Bn] = and out[B] = U for all B Bn */ out[Bn] = ; in[Bn] = use[Bn]; for each block B Bn do in[B] : = U - kill[B]; change : = true; while change do begin change : = false; for each block B Bn do begin out[B] : = s succ(B) in[s] oldin : = in[B] : = use[B] (out[B] - kill[B]) if in[B] oldin then change : = true end 39

Conservative Computation • The computed use set of busy expressions is a subset of the exact use set of busy expressions • The computed kill set of busy expressions is a superset of the exact kill set of busy expressions • The computed in and out sets of busy expressions is a subset of the exact in and out sets of busy expressions 40