CS 200 Algorithm Analysis HEAPSORT General characteristics Sorts

CS 200: Algorithm Analysis

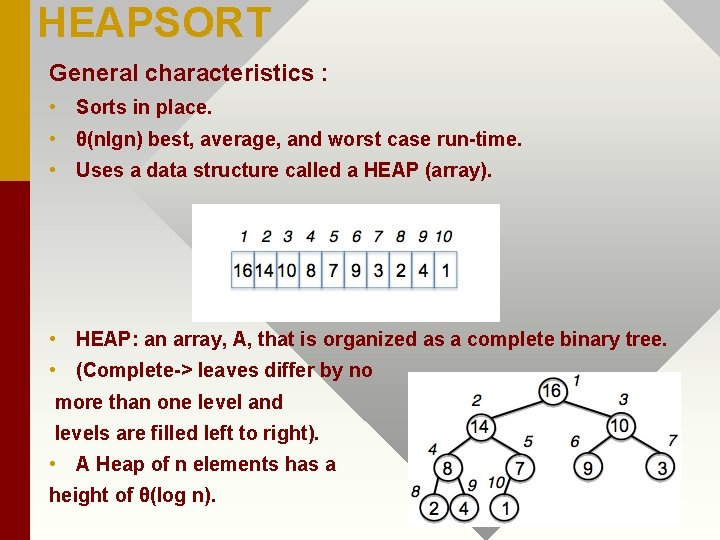
HEAPSORT General characteristics : • Sorts in place. • θ(nlgn) best, average, and worst case run-time. • Uses a data structure called a HEAP (array). • HEAP: an array, A, that is organized as a complete binary tree. • (Complete-> leaves differ by no more than one level and levels are filled left to right). • A Heap of n elements has a height of θ(log n).

• The HEAP is completely filled except for possibly the lowest level. The root is at A[1] and given the index i of a node, its Parent(i) can be computed as: Root of tree at position i = 1 • Parent(i) = ? return i / 2 {floor(i/2)} and its Left. Child(i) as: • Left(i) = ? return 2 i; and its Right. Child(i) as: • Right(i) = ? return 2 i + 1;

• A MAX HEAP must always satisfy the following property for all nodes i in the array. Min Heap defined analogously. – A[Parent(i)] >= A[i] => largest value in HEAP is stored in root and the value stored in the root of each subtree is >= the value in all descended nodes. • The height of a HEAP is the length of the longest simple path from the root to a leaf. (Show for example) => log n depth. • The height of a node is the length of the longest simple path from the node to a leaf. (Show an example). Height of 2? Height of 14? Height of 16?

Heap Operations • build_max_heap : produce a max-heap from an unordered array • max_heapify : correct a single violation of the heap property in a subtree at its root • insert, extract_max, heapsort

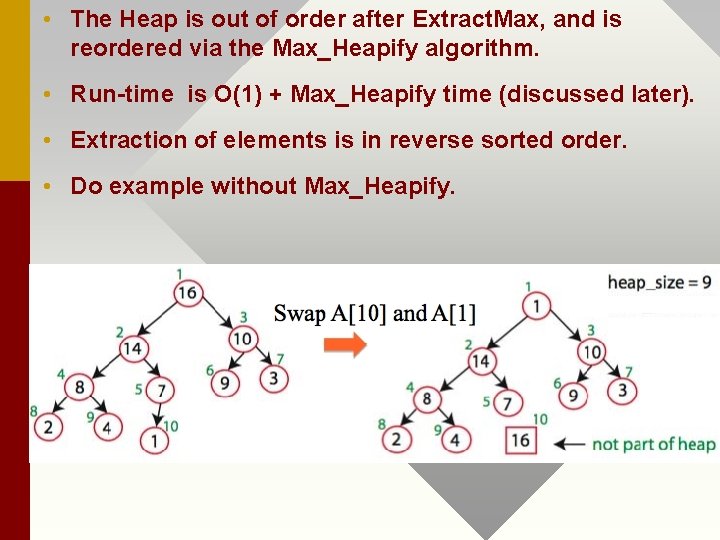
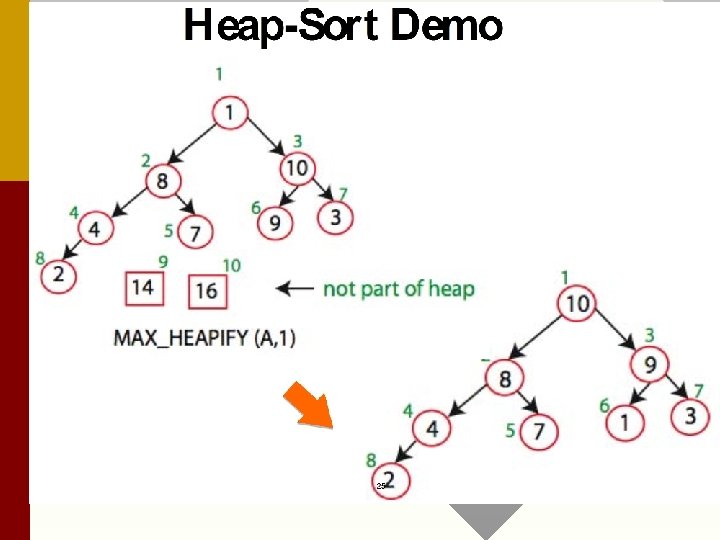
ALGORITHMS FOR HEAP • 1. Heap Operation : Extracting the maximum element from a HEAP. Extract. Max(A) //n is size of heap, A is array temp = A[1] = A[n] n = n-1; Max_Heapify(A, 1, n) return temp

• The Heap is out of order after Extract. Max, and is reordered via the Max_Heapify algorithm. • Run-time is O(1) + Max_Heapify time (discussed later). • Extraction of elements is in reverse sorted order. • Do example without Max_Heapify.

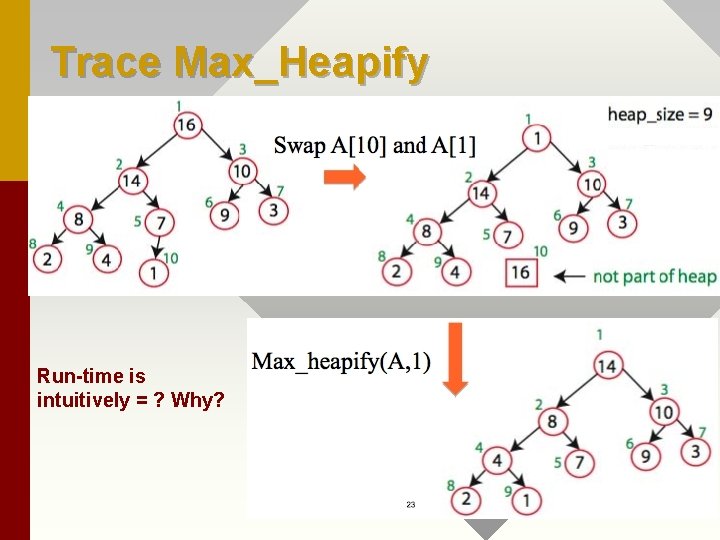
• 2. Heap Operation: to maintain HEAP property (elements float down to proper position in the HEAP). Max_Heapify(A, i, n) //position i, where reorder starts if (2 i <= n) and (A[2 i] > A[i]) then largest = 2 i // 2 i in bounds, left child largest else largest = i //current root largest if (2 i+1 <= n) and (A[2 i+1] > A[largest]) then largest = 2 i+1 //2 i+1 in bounds, right //child largest if largest != i then Swap(A[i], A[largest]); Max_Heapify(A, largest, n); Trace an example for algorithm next.

Trace Max_Heapify Run-time is intuitively = ? Why?

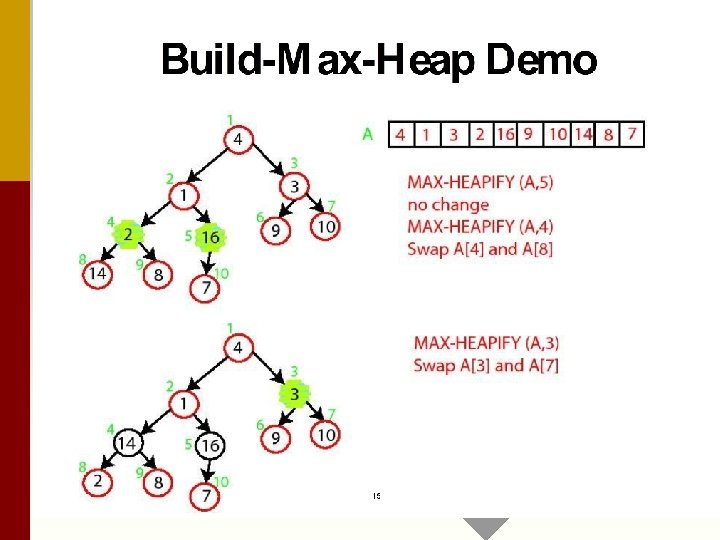
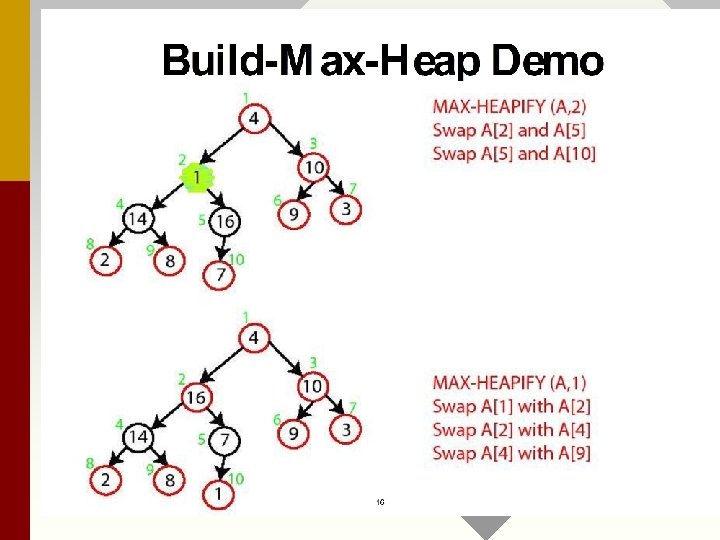
Build_Heap Operation : building a heap by converting an array. Build. Heap(A, n) for i = n / 2 downto 1 do Max_Heapify(A, i, n) Trace an example for algorithm, next slide set. Run-time is intuitively = _______? Why? Is this a tight upper bound? Is it possible to do better?

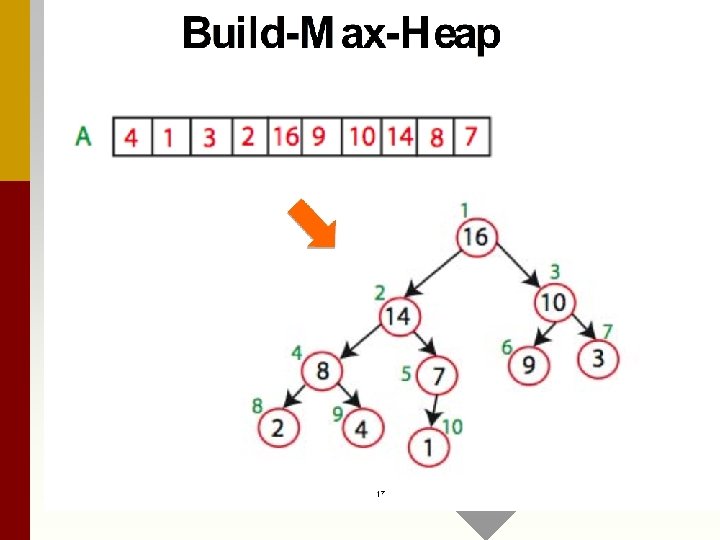
Converts A[1. . . n] to a max heap Build. Heap(A, n) for i = n / 2 downto 1 do Max_Heapify(A, i, n) Why start at n/2? Because elements A[n/2 + 1. . . n] are all leaves of the tree 2 i > n, for i > n/2 + 1. A single node is a max_heap! • Time? O(n log n) via simple analysis

Build_Heap Analysis Converts A[1. . . n] to a max heap Build. Heap(A, n) for i = n / 2 downto 1 do Max_Heapify(A, i, n) Observe that Max_Heapify takes O(1) time for nodes that are one level above the leaves, and in general, O(L) for the nodes that are L levels above the leaves. We have n/4 nodes with level 1, n/8 with level 2, and so on till we have one root node that is log n levels above the leaves.

Build_Heap Analysis Converts A[1. . . n] to a max heap Build. Heap(A, n) for i = n / 2 downto 1 do Max_Heapify(A, i, n) • Total amount of work in the for loop can be summed as: n/4 (1 c) + n/8 (2 c) + n/16 (3 c) +. . . + 1 (log n c) • Setting n/4 = 2 k and simplifying we get: c 2 k( 1/20 + 2/21 + 3/22 +. . . (k+1)/2 k ) • The term in () is bounded by a constant! • This means that Build_Max_Heap is O(n). Complete analysis on next slide.

Time to run MAX-HEAPIFY is linear in the height of the node it’s run on, h+1 and most nodes have small heights. There are ≤ n / 2 nodes of height h, and height of heap is log n. The time required by MAX-HEAPIFY when called on a node of height h is O(h), so the total cost of BUILD-MAX-HEAP is Evaluate the last summation by substituting x = 1/2 in the formula (A. 8) The running time of BUILD-MAX-HEAP is O(n).

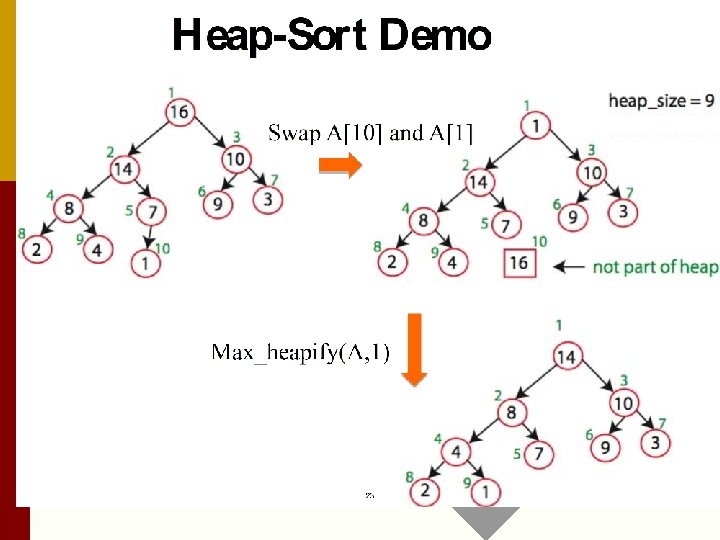
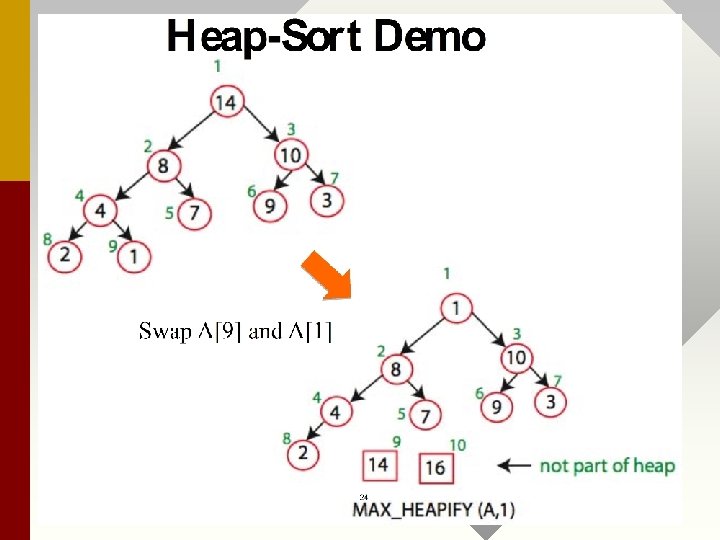
4. HEAPSORT Heap. Sort(A, n) Build. Heap(A, n) O(n) for i = n down to 2 do n-1 times swap(A[1], A[i] O(1) Max_Heapify(A, 1, i-1) O(lgn) T(n) = O(nlgn) Trace an example of algorithm.

Variations on HEAPS: • – min or max HEAP • – HEAP maintained as a k-ary tree vs. binary tree where each interior node has k children and heap property is maintained for each subtree.

DYNAMIC SETS • Set of elements that can grow, shrink with needs of an algorithm. • Elements of a dynamic set contain a KEY field (for identification) and a satellite data field (unused in the set operations). An element can be viewed as a record with 2 fields: key and data. • For the following operations assume that X is a pointer to an element record and that the record fields are already initialized.

DYNAMIC SET OPERATIONS • Insert(S, x) S <– S U {x} • Delete(S, x) S <– S - {x} • Minimum(S) return x in S with smallest key field • Search(S, k) return x in S with x->key = k The main issue is the data structure chosen to represent Dynamic Sets; different data structures will support and optimize different operations in the above list.

USING PRIORITY QUEUES AS DYNAMIC SETS A priority queue is a data structure for maintaining a dynamic set, S, of elements, each with an associated key value with ordering on the key. It supports: Insert(S, x) Minimum(S) Extract. Min(S) Decrease. Key(S, x, k) - discussed later for graph algorithms By examining priority queues it is obvious that this structure supports Insert and Extract. Min (Minimum set operation) but does not support the general delete operation. Ex: Max priority queue - process scheduler Min priority queue- event simulator by time of event

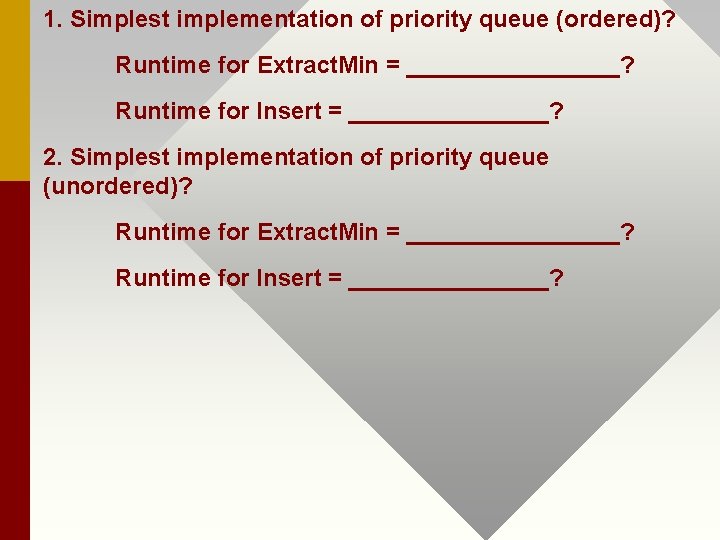
1. Simplest implementation of priority queue (ordered)? Runtime for Extract. Min = ________? Runtime for Insert = ________? 2. Simplest implementation of priority queue (unordered)? Runtime for Extract. Min = ________? Runtime for Insert = ________?

A more interesting implementation of a priority queue is via a HEAP. A min-HEAP with minimum maintained at root provides an excellent representation of a priority queue. This provides a good compromise between insertion and extraction because both can be done in ______? time. • Runtime of Minimum(S) _______? • Runtime of Extract. Min(S) ______? How does this work? How do we implement a general insert into a priority queue as a heap? What is its runtime?

Insertion into a Max_Heap as a Priority Queue Insert(S, x) n = n+1 i=n while(i > 1) and (S[i / 2] > x) do S[i] = S[i/2] i=i/2 A[i] = x T(n) = _______?

• Insert of key element is like insertion sort as elements are moved down tree to open up the right spot for insertion. • In worst case Insert traverses log n nodes as does heapify, but it compares parent only to 1 child not to both as in Heapify.

Summary • Heap – Heap algorithms – Heap analysis • Heap. Sort • Priority Queues – Heap as a priority queue