Heapsort A minimalists approach Jeff Chastine Heapsort Like

Heapsort A minimalist's approach Jeff Chastine

Heapsort • • Like MERGESORT, it runs in O(n lg n) Unlike MERGESORT, it sorts in place Based off of a “heap”, which has several uses The word “heap” doesn’t refer to memory management Jeff Chastine

The Heap • A binary heap is a nearly complete binary tree • Implemented as an array A • Two similar attributes: – length[A] is the size (number of slots) in A – heap-size[A] is the number of elements in A – Thus, heap-size[A] length[A] – Also, no element past A[heap-size[A]] is an element Jeff Chastine

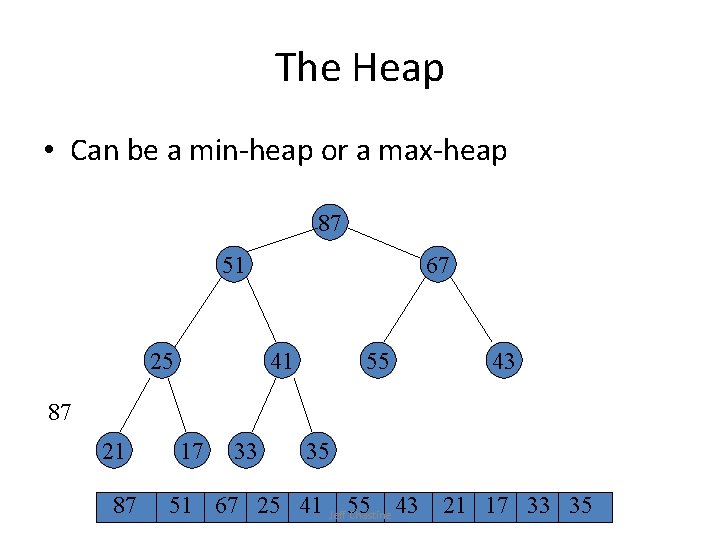
The Heap • Can be a min-heap or a max-heap 87 51 25 67 41 55 43 87 21 87 17 33 35 51 67 25 41 Jeff 55 43 Chastine 21 17 33 35

Simple Functions PARENT(i) return (i/2) LEFT(i) return (2 i) RIGHT(i) return (2 i + 1) Jeff Chastine

Properties • Max-heap property: – A[PARENT(i)] A[i] • Min-heap property: – A[PARENT(i)] A[i] • Max-heaps are used for sorting • Min-heaps are used for priority queues (later) • We define the height of a node to be the longest path from the node to a leaf. • The height of the tree is (lg n) Jeff Chastine

MAX-HEAPIFY • This is the heart of the algorithm • Determines if an individual node is smaller than its children • Parent swaps with largest child if that child is larger • Calls itself recursively • Runs in O(lg n) or O(h) Jeff Chastine

HEAPIFY MAX-HEAPIFY (A, i) l ← LEFT (i) r ← RIGHT(i) if l ≤ heap-size[A] and A[l] > A[i] then largest ← l else largest ← i if r ≤ heap-size[A] and A[r]>A[largest] then largest ← r if largest ≠ i then exchange A[i] with A[largest] MAX-HEAPIFY (A, largest) Jeff Chastine

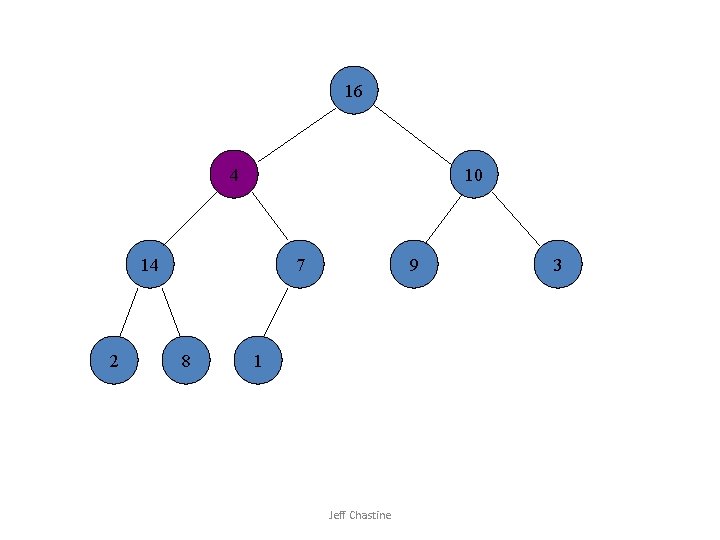
16 4 10 14 2 7 8 9 1 Jeff Chastine 3

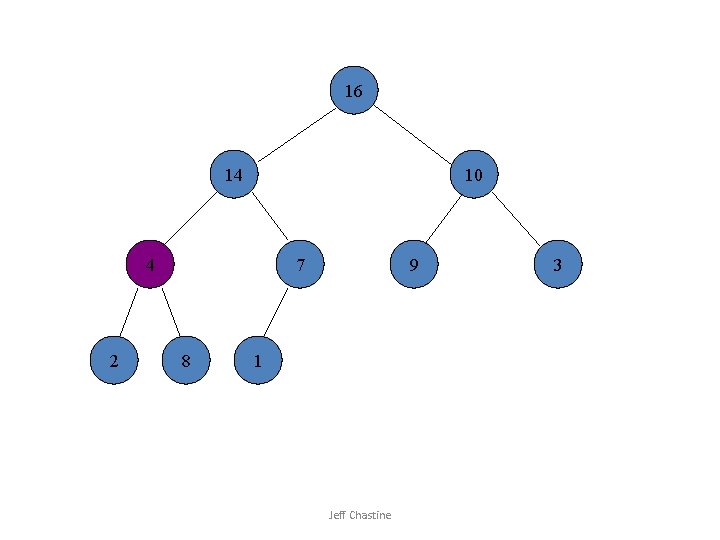
16 14 10 4 2 7 8 9 1 Jeff Chastine 3

16 14 10 8 2 7 4 9 1 Jeff Chastine 3

Of Note • The children’s subtrees each have size at most 2 n/3 – when the last row is exactly ½ full • Therefore, the running time is: T (n) = T(2 n/3) + (1) = O(lg n) Jeff Chastine

BUILD-HEAP • Use MAX-HEAPIFY in bottom up manner • Why does the loop start at length[A]/2? • At the start of each loop, each node i is the root of a max-heap! BUILD-HEAP (A) heap-size[A] ← length[A] for i ← length[A]/2 downto 1 do MAX-HEAPIFY(A, i) Jeff Chastine

Analysis of Building a Heap • Since each call to MAX-HEAPIFY costs O(lg n) and there are O(n) calls, this is O(n lg n). . . • Can derive a tighter bound: do all nodes take log n time? • Has at most n/2 h+1 nodes at any height (the more the height, the less nodes there are) • It takes O(h) time to insert a node of height h. Jeff Chastine

Sum up the work at each level Height h is logarithmic The number of nodes at height h Multiplied by their height • Thus, the running time is 2 n = O(n) Jeff Chastine

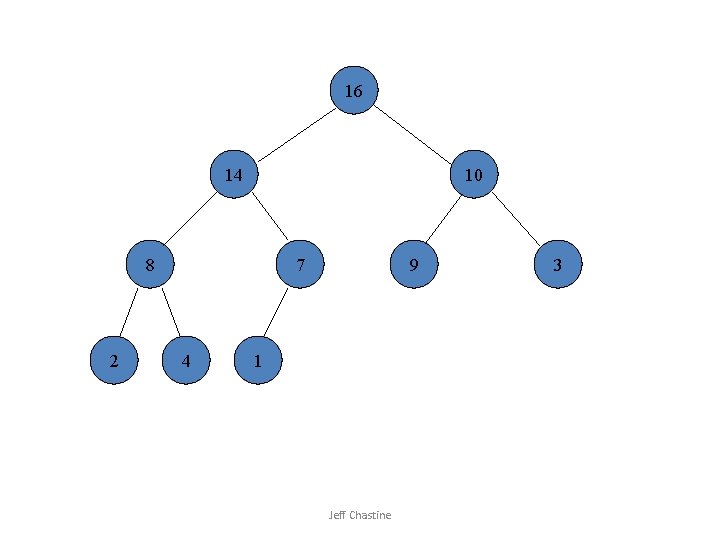
HEAPSORT (A) BUILD-HEAP(A) for i ← length[A] downto 2 do exchange A[1] with A[i] heap-size[A] ← heap-size[A] - 1 MAX-HEAPIFY(A, 1) Jeff Chastine

16 14 10 8 2 7 4 9 1 Jeff Chastine 3

1 14 10 8 2 7 4 9 16 Swap A[1] A[i] Jeff Chastine 3

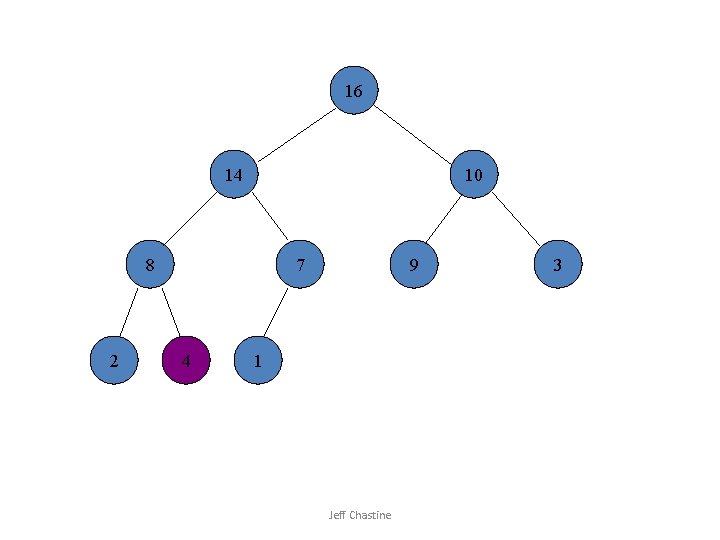
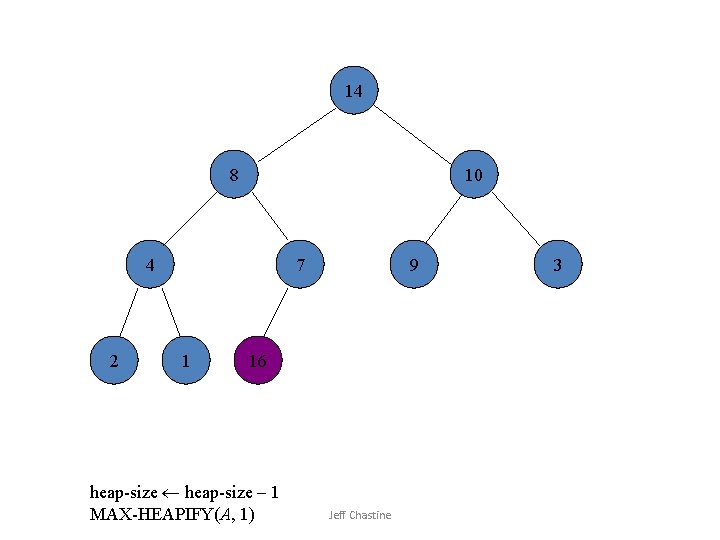
14 8 10 4 2 7 1 9 16 heap-size – 1 MAX-HEAPIFY(A, 1) Jeff Chastine 3

1 8 10 4 2 7 14 9 16 Swap A[1] A[i] Jeff Chastine 3

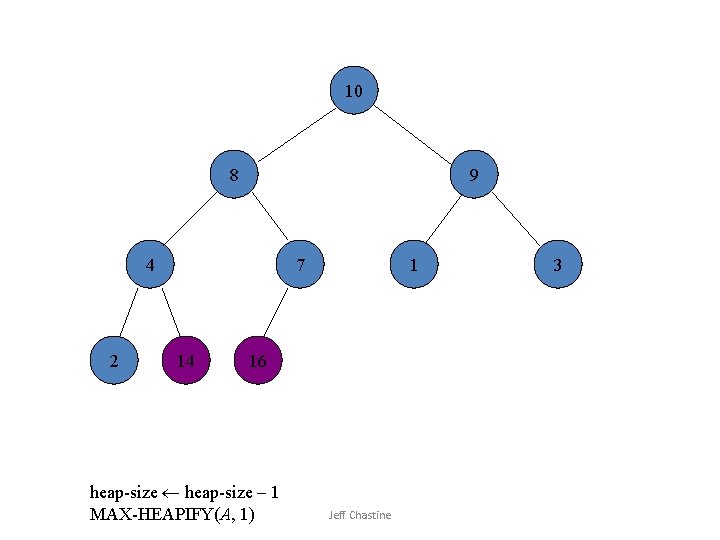
10 8 9 4 2 7 14 1 16 heap-size – 1 MAX-HEAPIFY(A, 1) Jeff Chastine 3

2 8 9 4 10 7 14 1 16 Swap A[1] A[i] Jeff Chastine 3

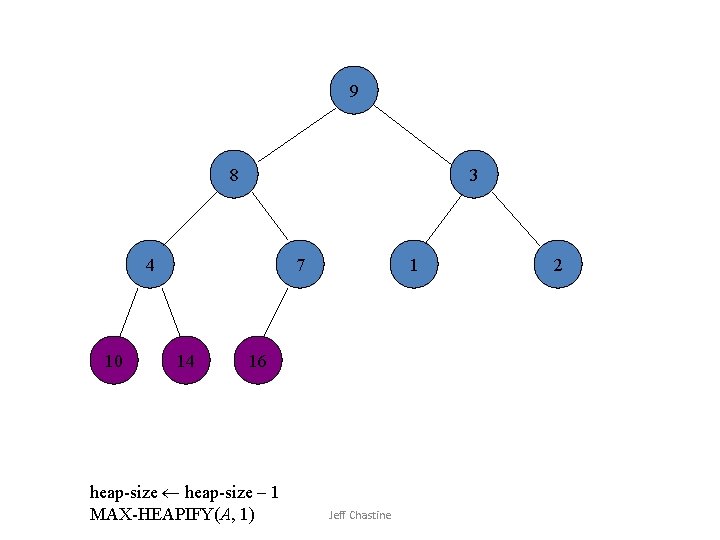
9 8 3 4 10 7 14 1 16 heap-size – 1 MAX-HEAPIFY(A, 1) Jeff Chastine 2

2 8 3 4 10 7 14 1 16 Swap A[1] A[i] Jeff Chastine 9

8 7 3 4 10 2 14 1 16 heap-size – 1 MAX-HEAPIFY(A, 1) Jeff Chastine 9

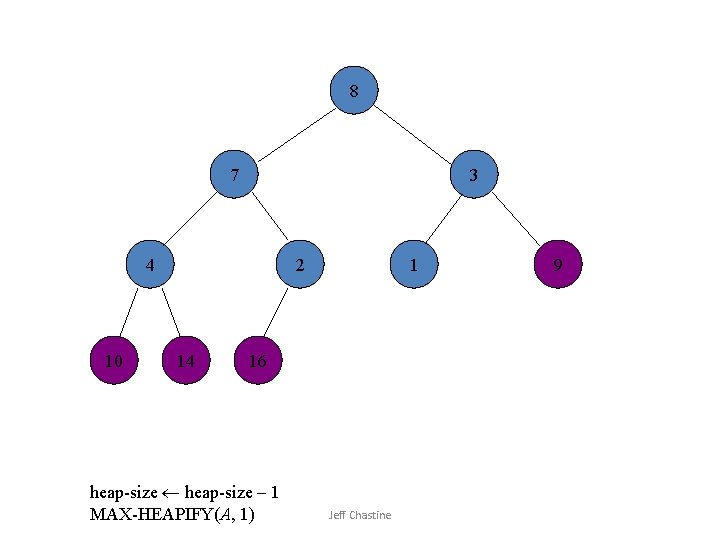
1 7 3 4 10 2 14 8 16 Swap A[1] A[i] Jeff Chastine 9

7 4 3 1 10 2 14 8 16 heap-size – 1 MAX-HEAPIFY(A, 1) Jeff Chastine 9

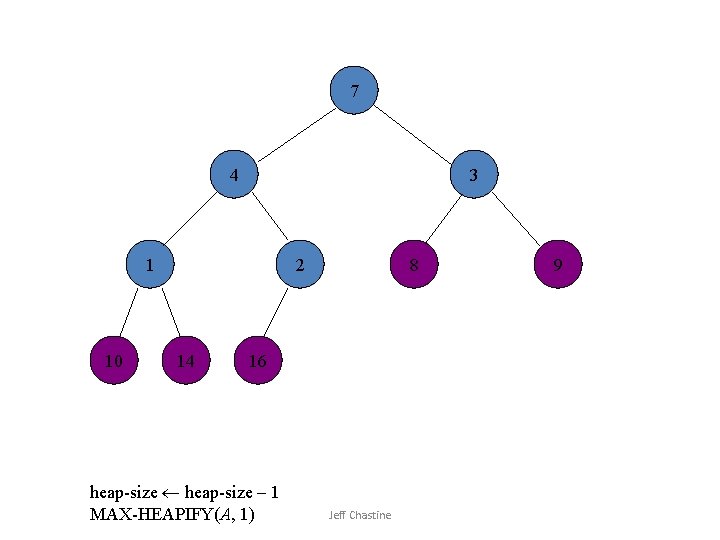
2 4 3 1 10 7 14 8 16 Swap A[1] A[i] Jeff Chastine 9

4 2 3 1 10 7 14 8 16 heap-size – 1 MAX-HEAPIFY(A, 1) Jeff Chastine 9

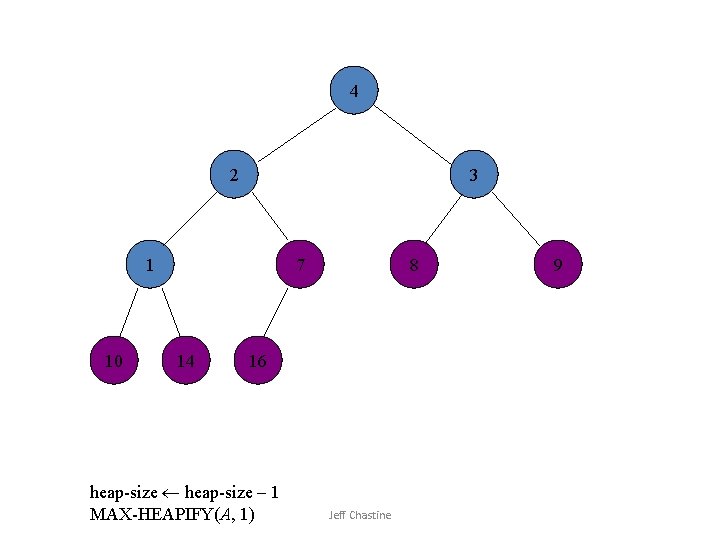
1 2 3 4 10 7 14 8 16 Swap A[1] A[i] Jeff Chastine 9

3 2 1 4 10 7 14 8 16 heap-size – 1 MAX-HEAPIFY(A, 1) Jeff Chastine 9

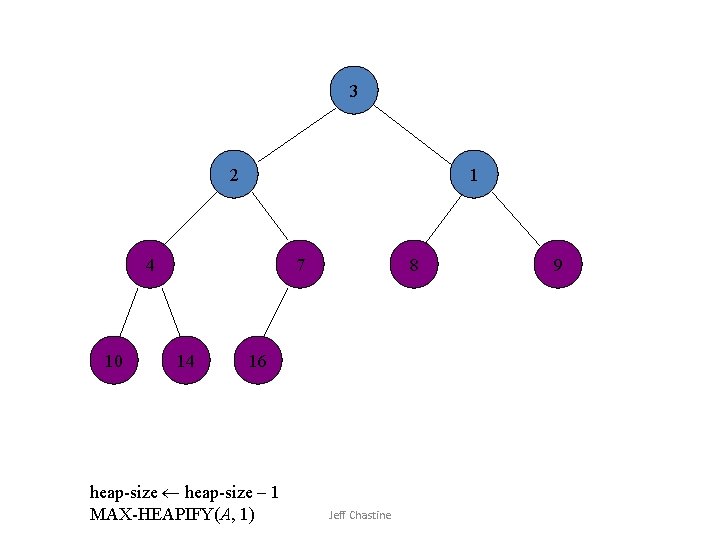
1 2 3 4 10 7 14 8 16 Swap A[1] A[i] Jeff Chastine 9

2 1 3 4 10 7 14 8 16 heap-size – 1 MAX-HEAPIFY(A, 1) Jeff Chastine 9

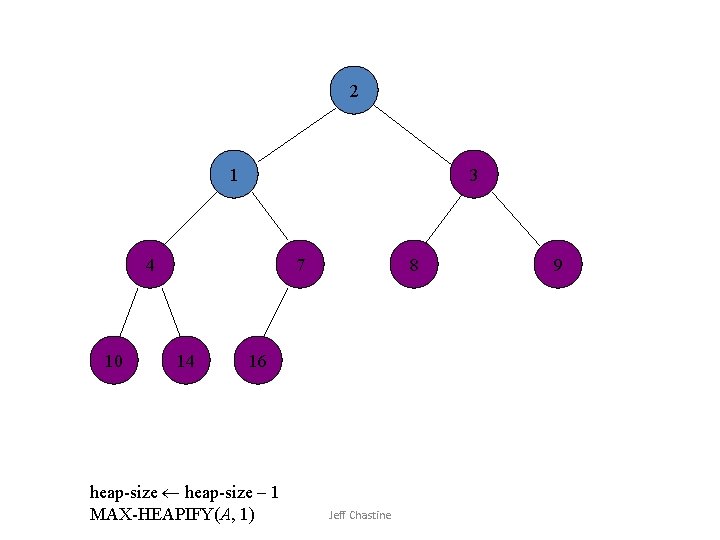
1 2 3 4 10 7 14 8 16 Swap A[1] A[i] Jeff Chastine 9

1 2 3 4 10 7 14 8 16 heap-size – 1 MAX-HEAPIFY(A, 1) Jeff Chastine 9

Priority Queues • A priority queue is a heap that uses a key • Common in operating systems (processes) • Supports HEAP-MAXIMUM, EXTRACT-MAX, INCREASE-KEY, INSERT HEAP-MAXIMUM (A) 1 return A[1] Jeff Chastine

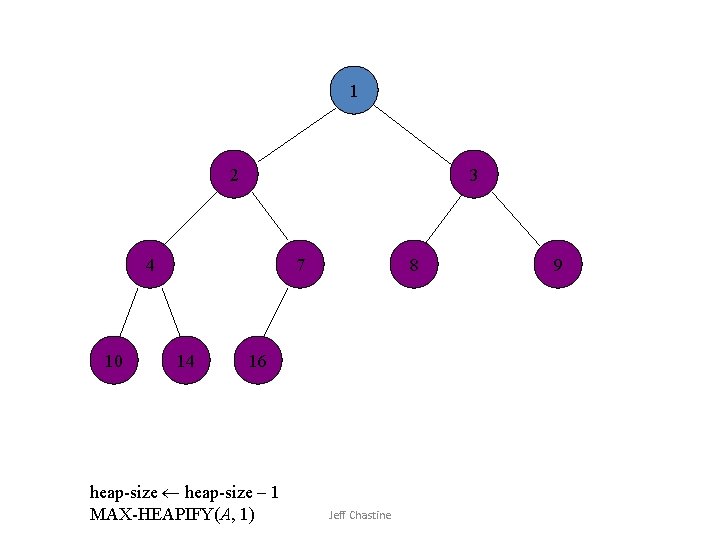
HEAP-EXTRACT-MAX (A) 1 if heap-size[A] < 1 2 then error “heap underflow” 3 max A[1] 4 A[1] A[heap-size[A]] 5 heap-size[A] – 1 6 MAX-HEAPIFY (A, 1) 7 return max Jeff Chastine

HEAP-INCREASE-KEY(A, i, key) 1 if key < A[i] 2 then error “new key smaller than current” 3 A[i] key 4 while i > 1 and A[PARENT(i)] < A[i] 5 do exchange A[i] A[PARENT(i)] 6 i PARENT(i) Note: runs in O(lg n) Jeff Chastine

MAX-HEAP-INSERT (A, key) 1 heap-size[A] + 1 2 A[heap-size[A]] - 3 HEAP-INCREASE-KEY(A, heap-size[A], key) Jeff Chastine