Heapsort Algorithm Design Analysis 8 In the last

Heapsort Algorithm : Design & Analysis [8]

In the last class… n n n Mergesort Worst Case Analysis of Mergesort Lower Bound for Average Behavior n n n Worst Case Average Behavior Lower Bound of Key Comparison Based Sorting Algorithm

Heapsort n n n Heap Structure and Patial Order Tree Property The Strategy of Heapsort Keep the Partial Order Tree Property after the maximal element is removed Constructing the Heap Complexity of Heapsort Accelerated Heapsort

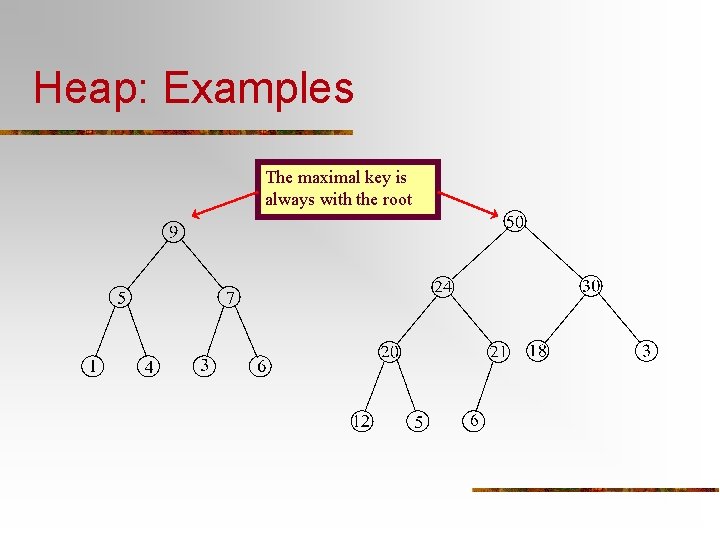
Heap: a Data Structure n A binary tree T is a heap structure if: n T is complete at least through depth h-1 A are heap n All leaves atis: depth h or h-1 n All path to a leafstructure, of depth h are to the left of all A heap path to asatisfying leaf of depth h-1 n order tree property Partial order. Partial tree property n A tree T is a (maximizing) partial order tree if and only if the key at any node is greater than or equal to the keys at each of its children(if it has any).

Heap: Examples The maximal key is always with the root

Heapsort: the Strategy heap. Sort(E, n) Construct H from E, the set of n elements to be sorted; for (i=n; i 1; i--) cur. Max = get. Max(H); delete. Max(H); E[i] = cur. Max delete. Max(H) Copy the rightmost element on the lowest level of H into K; Delete the rightmost element on the lowest level of H; fix. Heap(H, K)

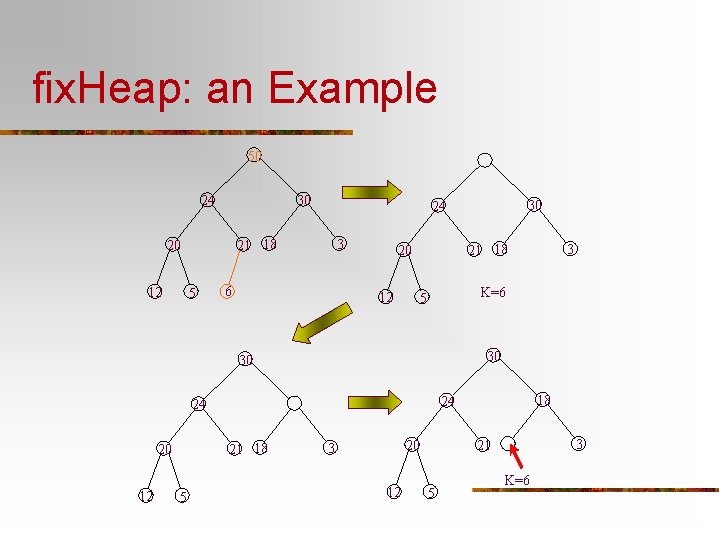
Fix. Heap: Keeping the Partial Order Tree Property Input: A nonempty binary tree H with a “vacant” root and its two subtrees in partial order. An element K to be inserted. n Output: H with K inserted and satisfying the partial order tree property. One comparison: n Procesure: larger. Sub. Heap is left- or rightfix. Heap(H, K) Subtree(H), the one with larger key if (H is a leaf) insert K in root(H); at its root. else Special case: right. Subtree is empty Set larger. Sub. Heap; if (K. key root(larger. Sub. Heap). key) insert K in root(H) else insert root(larger. Sub. Heap) in root(H); Recursion fix. Heap(larger. Sub. Heap, K); “Vacant” moving down return n

fix. Heap: an Example 50 30 24 21 18 20 12 5 3 6 21 18 20 12 30 12 5 18 24 24 21 18 3 K=6 5 30 20 30 24 20 3 12 3 21 5 K=6

Worst Case Analysis for fix. Heap n n n 2 comparisons at most in one activation of the procedure The tree height decreases by one in the recursive call So, 2 h comparisons are needed in the worst case, where h is the height of the tree One comparison: Procesure: larger. Sub. Heap is left- or rightfix. Heap(H, K) Subtree(H), the one with larger key if (H is a leaf) insert K in root(H); at its root. else Special case: right. Subtree is empty Set larger. Sub. Heap; if (K. key root(larger. Sub. Heap). key) insert K in root(H) else insert root(larger. Sub. Heap) in root(H); Recursion fix. Heap(larger. Sub. Heap, K); “Vacant” moving down return n

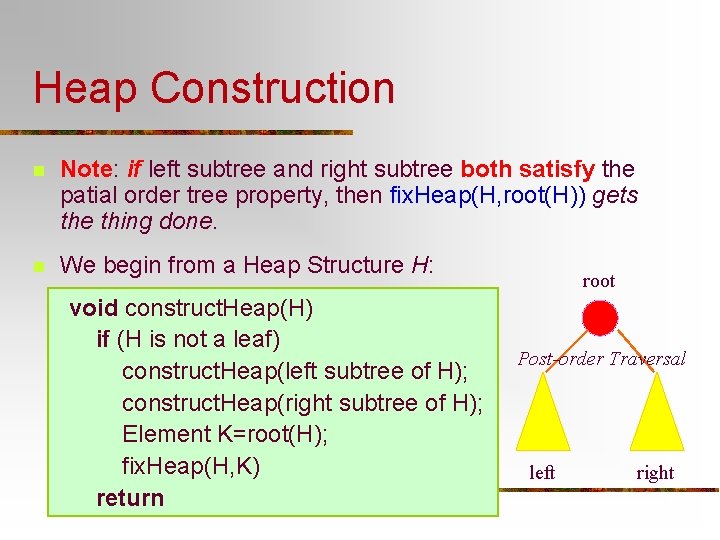
Heap Construction n Note: if left subtree and right subtree both satisfy the patial order tree property, then fix. Heap(H, root(H)) gets the thing done. n We begin from a Heap Structure H: void construct. Heap(H) if (H is not a leaf) construct. Heap(left subtree of H); construct. Heap(right subtree of H); Element K=root(H); fix. Heap(H, K) return root Post-order Traversal left right

Correctness of construct. Heap n Specification Input: A heap structure H, not necessarily having the partial order tree property. n Output: H with the same nodes rearranged to satisfy the partial order tree property. H is a leaf: base case, satisfied trivially. void construct. Heap(H) if (H is not a leaf) construct. Heap(left subtree of H); construct. Heap(right subtree of H); Element K=root(H); Preconditions hold respectively? fix. Heap(H, K) return n Postcondition of construct. Heap satisfied?

The Heap Is Constructed in Linear Time! Number of nodes in right subheap n n The recursion equation: Cost of fix. Heap W(n)=W(n-r-1)+W(r)+2 lg(n) A special case: H is a complete binary tree: n The size N=2 d-1, and N/2<n N, so W(n) W(N), n Note: W(N)=2 W((N-1)/2)+2 lg(N) n The Master Theorem applys, with b=c=2, and the critical exponent E=1, f(N)=2 lg(N) n n n Note: L’Hôpital’s Rule When 0< <1, this limit is equal to zero So, 2 lg(N) (N E- ), case 1 satisfied, we have W(N) (N), so, W(n)

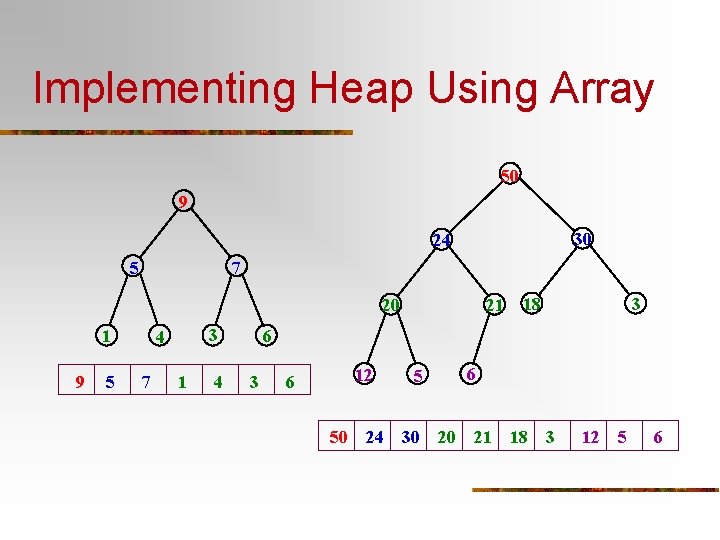
Implementing Heap Using Array 50 9 30 24 5 7 20 1 9 5 3 4 7 1 4 21 18 3 6 3 12 6 50 24 6 5 30 20 21 18 3 12 5 6

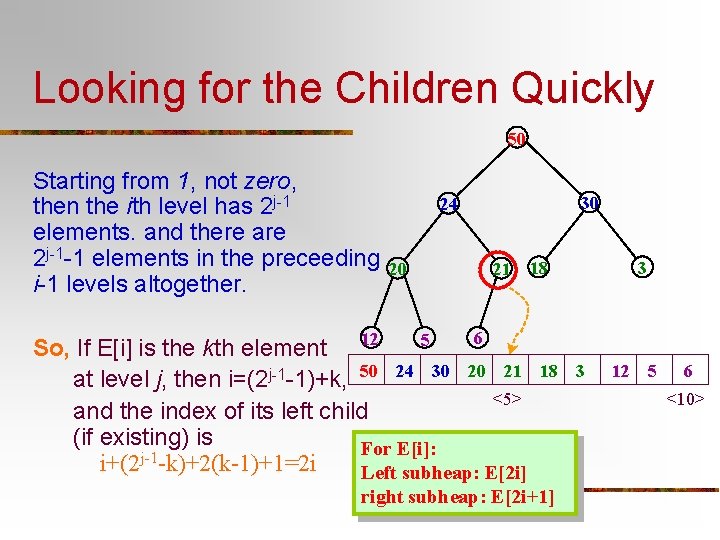
Looking for the Children Quickly 50 Starting from 1, not zero, then the ith level has 2 j-1 elements. and there are 2 j-1 -1 elements in the preceeding i-1 levels altogether. 30 24 20 21 18 3 6 5 So, If E[i] is the kth element 12 at level j, then i=(2 j-1 -1)+k, 50 24 30 20 21 <5> and the index of its left child (if existing) is For E[i]: j-1 i+(2 -k)+2(k-1)+1=2 i Left subheap: E[2 i] 18 right subheap: E[2 i+1] 3 12 5 6 <10>

In-space Implementation of Heapsort Heap implemented as a array (initial) E[1]: The largest key to be moved to E[n] K: removed to be inserted Sorted portion E[1]: The largest key in current heap, to be moved to E[heapsize] K: removed to be inserted Current heap: processed by fix. Heap

Heapsort: the Algorithm n n n Input: E, an unsorted array with n(>0) elements, indexed from 1 Sorted E, in nondecreasing order Procedure: New Version void heap. Sort(Element[] E, int n) int heapsize construct. Heap(E, n, root) for (heapsize=n; heapsize 2; heapsize--; ) Element cur. Max=E[1]; Element K=E[heapsize]; fix. Heap(E, heapsize-1, 1, K); E[heapsize]=cue. Max; return;

Worst Case Analysis of Heapsort n We have: n It has been known that: n Recall that: n So, W(n) 2 nlgn + (n), that is W(n) (nlogn) Coefficient doubles that of merge. Sort approximately

heap. Sort: the Right Choice n n For heap. Sort, W(n) (nlgn) Of course, A(n) (nlgn) More good news: heap. Sort is an in-space algorithm It’ll be more competitive if only the coefficient of the leading term can be decreased to 1

Number of Comparisons in fix. Heap 2 comparisons are Procesure: done in filtering fix. Heap(H, K) down for one level. if (H is a leaf) insert K in root(H); else Set larger. Sub. Heap; if (K. key root(larger. Sub. Heap). key) insert K in root(H) else insert root(larger. Sub. Heap) in root(H); fix. Heap(larger. Sub. Heap, K); return

A One-Comparison-per-Level Fixing n Bubble-Up Heap Algorithm: void bubble. Up. Heap(Element []E, int root, Element K, int vacant) if (vacant==root) E[vancant]=K; else Bubbling up from int parent=vacant/2; vacant through to the if (K. key E[parent]. key) root, recursively E[vacant]=K else E[vacant]=E[parent]; bubble. Up. Heap(E, root, K, parent);

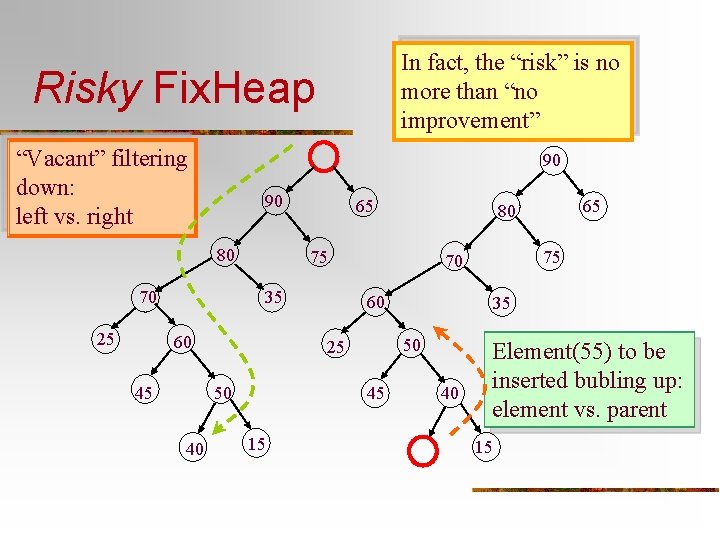
In fact, the “risk” is no more than “no improvement” Risky Fix. Heap “Vacant” filtering down: left vs. right 90 90 80 70 25 65 75 35 60 45 50 40 60 35 50 45 15 75 70 25 65 80 40 Element(55) to be inserted bubling up: element vs. parent 15

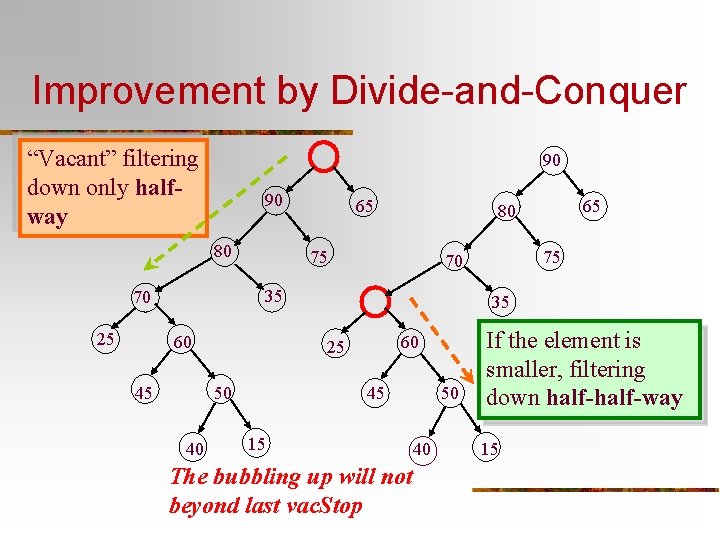
Improvement by Divide-and-Conquer “Vacant” filtering down only halfway 90 90 80 75 60 45 40 75 70 35 60 25 50 65 80 35 70 25 65 45 15 The bubbling up will not beyond last vac. Stop 50 40 If the element is smaller, filtering down half-way 15

Depth Bounded Filtering Down int promote(Element [ ] E, int h. Stop, int vacant, int h) int vac. Stop; Depth Bound if (h h. Stop) vac. Stop=vacant; else if (E[2*vacant]. key E[2*vacant+1]. key) E[vacant]=E[2*vacant+1]; vac. Stop=promote(E, h. Stop, 2*vacan+1, h-1); else E[vacant]=E[2*vacant]; vac. Stop=promote(E, h. Stop, 2*vacant, h-1); return vac. Stop

fix. Heap Using Divide-and-Conquer void fix. Heap. Fast(Element [ ] E, Element K, int vacant, int h) //h= lg(n+1)/2 in uppermost call if (h 1) Process heap of height 0 or 1; else int h. Stop=h/2; int vac. Stop=promote(E, h. Stop, vacant, h); int vac. Parent=vac. Stop/2; if (E[vac. Parent]. key K. key) E[vac. Stop]=E[vac. Parent]; bubble. Up. Heap(E, vacant, K, vac. Parent); else fix. Heap. Fast(E, K, vac. Stop, h. Stop)

Number of Comparisons in the Worst Case for Accelerated fix. Heap n n Moving the vacant one level up or down need one comparison exactly in promote or bubble. Up. Heap. In a cycle, t calls of promote and 1 call of bubble. Up. Heap are excuted at most. So, the number of comparisons in promote and bubble. Up. Heap calls are: n At most, lg(h) checks for reverse direction are excecuted. So, the number of comparisons in a cycle is at most h+lg(h) n So, for accelerated heap. Sort: W(n)=nlgn+ (nloglogn)

Recursion Equation of Accelerated heap. Sort The recurrence equation about h, which is about lg(n+1) Assuming T(h) h, then:

Solving the Recurrence Equation by Recursive Tree For sorting a sequence of size n, n cycles of fix. Heap T(n) h/2 +1 are executed, so: n. (h+ lg(h+1) ) T( n/2 ) h/4 +1 lg(h+1) levels T( n/4 ) h/8 +1 So, the total cost is: h+ lg(h+1) T(1) 1+1

Inductive Proof n n The recurrence equation for fix. Heap. Fast: Proving the following solution by induction: T(h) = h+ lg(h+1) n According to the recurrence equation: T(h+1)= (h+1)/2 +1+T( (h+1)/2 ) n Applying the inductive assumption to the last term: T(h+1)= (h+1)/2 +1+ (h+1)/2 + lg( (h+1)/2 +1) (It can be proved that for any positive integer: lg( (h)/2 +1) +1= lg(h+1) ) The sum is h+1

Home Assignment n pp. 213 n n 4. 37 4. 38 4 -39 4 -44