Coordinate Geometry in the x y plane Introduction

Coordinate Geometry in the (x, y) plane

Introduction • This chapter focuses on Parametric equations • Parametric equations split a ‘Cartesian’ equation into an x and y ‘component’ • They are used to model projectiles in Physics • This in turn allows video game programmers to create realistic physics engines in their games…

Teachings for Exercise 2 A

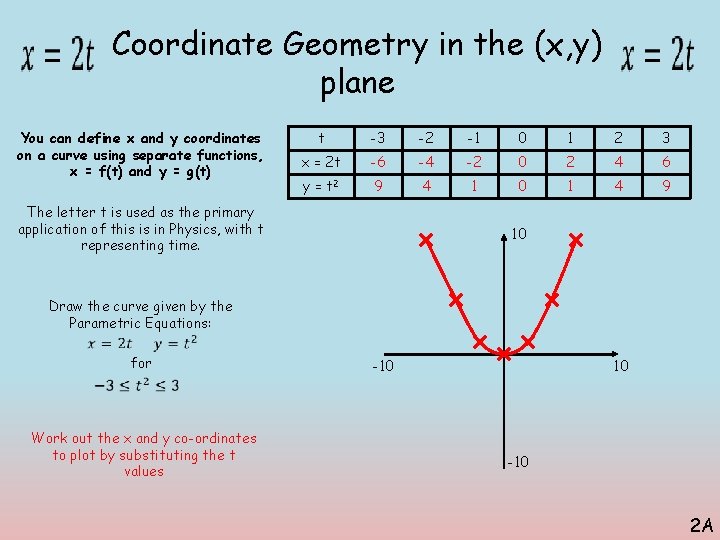
Coordinate Geometry in the (x, y) plane You can define x and y coordinates on a curve using separate functions, x = f(t) and y = g(t) t -3 -2 -1 0 1 2 3 x = 2 t -6 -4 -2 0 2 4 6 y = t 2 9 4 1 0 1 4 9 The letter t is used as the primary application of this is in Physics, with t representing time. 10 Draw the curve given by the Parametric Equations: for -10 10 Work out the x and y co-ordinates to plot by substituting the t values -10 2 A

Coordinate Geometry in the (x, y) plane You can define x and y coordinates on a curve using separate functions, x = f(t) and y = g(t) Divide by 2 A curve has parametric equations: Find the Cartesian equation of the curve Rewrite t in terms of x, and then substitute it into the y equation… Replace t with x/2 Simplify 2 A

Coordinate Geometry in the (x, y) plane You can define x and y coordinates on a curve using separate functions, x = f(t) and y = g(t) A curve has parametric equations: Find the Cartesian equation of the curve Rewrite t in terms of x, and then substitute it into the y equation… Multiply by (t + 1) Divide by x Subtract 1 Replace t 1 = x /x Put the fractions together Simplify 2 A

Teachings for Exercise 2 B

Coordinate Geometry in the (x, y) plane You need to be able to use Parametric equations to solve problems in coordinate geometry The diagram shows a sketch of the curve with Parametric equations: A The curve meets the x-axis at the points A and B. Find their coordinates. At points A and B, y = 0 Sub y = 0 in to find t at these points So t = ± 2 Sub this into the x equation to find the x-coordinates of A and B are (-3, 0) and (1, 0) B y=0 + t 2 Remember both answers Sub in t = 2 Sub in t = -2 2 B

Coordinate Geometry in the (x, y) plane You need to be able to use Parametric equations to solve problems in coordinate geometry A curve has Parametric equations: where a is a constant. Given that the curve passes through (2, 0), find the value of a. We know there is a coordinate where x = 2 and y = 0, Sub y = 0 into its equation Since we know that at (2, 0), x = 2 and t = -2, we can put these into the x equation to find a y=0 The ‘a’ part cannot be 0 or there would not be any equations! Subtract 8 Cube root So the t value at the coordinate (2, 0) is -2 Sub in x and t values Divide by -2 The actual equations with a = -1 2 B

Coordinate Geometry in the (x, y) plane You need to be able to use Parametric equations to solve problems in coordinate geometry A curve is given Parametrically by: The line x + y + 4 = 0 meets the curve at point A. Find the coordinates of A. The first thing we need to do is to find the value of t at coordinate A Sub x and y equations into the line equation Replace x and y with their equations ‘Tidy up’ Factorise Find t So t = -2 where the curve and line meet (point A) We know an equation for x and one for y, and we now have the t value to put into them… Sub t = -2 The curve and line meet at (4, -8) 2 B

Teachings for Exercise 2 C

Coordinate Geometry in the (x, y) plane You need to be able to convert Parametric equations into Cartesian equations A Cartesian equation is just an equation of a line where the variables used are x and y only A curve has Parametric equations: Isolate sint Isolate cost Replace sint and cost a) Find the Cartesian equation of the curve We need to eliminate t from the equations 5 Centre = (2, -3) Radius = 1 b) Sketch the curve The equation is that of a circle Think about where the centre will be, and its radius -5 5 -5 2 C

Coordinate Geometry in the (x, y) plane You need to be able to convert Parametric equations into Cartesian equations Square A Cartesian equation is just an equation of a line where the variables used are x and y only Rearrange A curve has Parametric equations: Replace sin 2 t with x 2 a) Find the Cartesian equation of the curve We need to eliminate t from the equations Use the double angle formula from C 3 Replace sint with x Square root We can now replace cos t Another way of writing this (by squaring the whole of each side) 2 C

Teachings for Exercise 2 D

Coordinate Geometry in the (x, y) plane You need to be able to find the area under a curve when it is given by Parametric equations The Area under a curve is given by: By the Chain rule: Integrate the equation with respect to x Integrate the whole expression with respect to t (Remember you don’t have to do anything with the dt at the end!) y multiplied by dx/dt (x differentiated with respect to t) 2 D

Coordinate Geometry in the (x, y) plane You need to be able to find the area under a curve when it is given by Parametric equations A curve has Parametric equations: Differentiate Sub in y and dx/ dt Work out: Multiply Remember to Integrate now. A common mistake is forgetting to! Sub in the two limits Work out the answer! 2 D

Coordinate Geometry in the (x, y) plane You need to be able to find the area under a curve when it is given by Parametric equations R The diagram shows a sketch of the curve with Parametric equations: 0 The curve meets the x-axis at x = 0 and x = 9. The shaded region is bounded by the curve and the x-axis. a) Find the value of t when: i) x=0 ii) x = 9 b) Find the Area of R i) 9 x=0 Square root ii) x=9 Square root t≥ 0 Normally when you integrate to find an area, you use the limits of x, and substitute them into the equation When integrating using Parametric Equations, you need to use the limits of t (since we integrate with respect to t, not x) The limits of t are worked out using the limits of x, as we have just done 2 D

Coordinate Geometry in the (x, y) plane You need to be able to find the area under a curve when it is given by Parametric equations R The diagram shows a sketch of the curve with Parametric equations: The curve meets the x-axis at x = 0 and x = 9. The shaded region is bounded by the curve and the x-axis. a) Find the value of t when: i) x=0 ii) x = 9 b) Find the Area of R Limits of t are 3 and 0 0 Differentiate 9 Sub in y and dx/ dt Multiply INTEGRATE!! (don’t forget!) Sub in 3 and 0 Work out the answer 2 D

Coordinate Geometry in the (x, y) plane You need to be able to find the area under a curve when it is given by Parametric equations The diagram shows a sketch of the curve with Parametric equations: 0 8 Calculate the finite area inside the loop… We have the x limits, we need the t limits x=0 Halve and square root x=8 Halve and square root Our t values are 0 and ± 2 We have 3 t values. We now have to integrate twice, once using 2 and once using -2 One gives the area above the x-axis, and the other the area below (in this case the areas are equal but only since the graph is symmetrical) 2 D

Coordinate Geometry in the (x, y) plane You need to be able to find the area under a curve when it is given by Parametric equations The diagram shows a sketch of the curve with Parametric equations: Differentiate Sub in y and dx/ dt Calculate the finite area inside the loop… The t limits are 0 and ± 2 Multiply out INTEGRATE!!!! Sub in 0 and -2 0 8 At this point we can just double the answer, but just to show you the other pairs give the same answer (as the graph was symmetrical) 2 D

Coordinate Geometry in the (x, y) plane You need to be able to find the area under a curve when it is given by Parametric equations The diagram shows a sketch of the curve with Parametric equations: Differentiate Sub in y and dx/ dt Calculate the finite area inside the loop… The t limits are 0 and ± 2 Multiply out INTEGRATE!!!! Sub in 0 and -2 0 Here you end up subtracting a negative… 8 Double 2 D

Summary • We have learnt what Parametric equations are • We have seen how to write them as a Cartesian equation • We have seen how to calculate areas beneath Parametric equations