Coordinate Geometry in the x y plane After







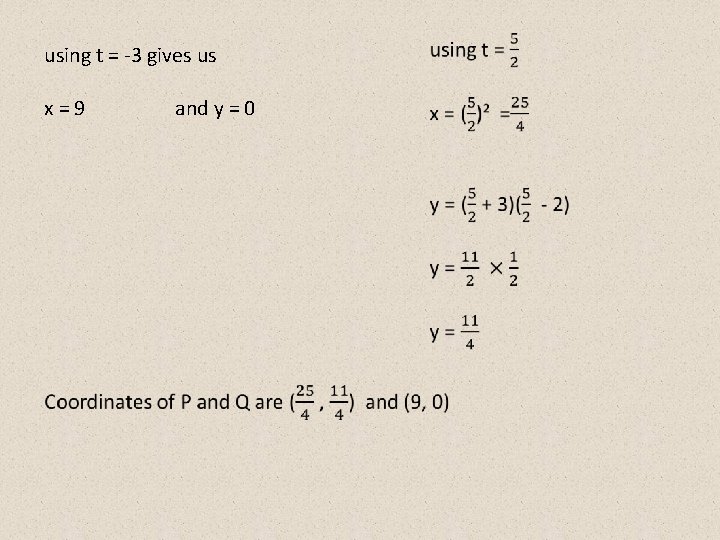






- Slides: 16

Coordinate Geometry in the (x, y) plane

After completing this chapter you should be able to: • Sketch the graph of a curve given it’s parametric equation • Use the parametric equation of the curve to solve various problems including the intersection of a line with a curve • Convert parametric equations into a Cartesian form • Find the area under a curve whose equation is expressed in parametric form

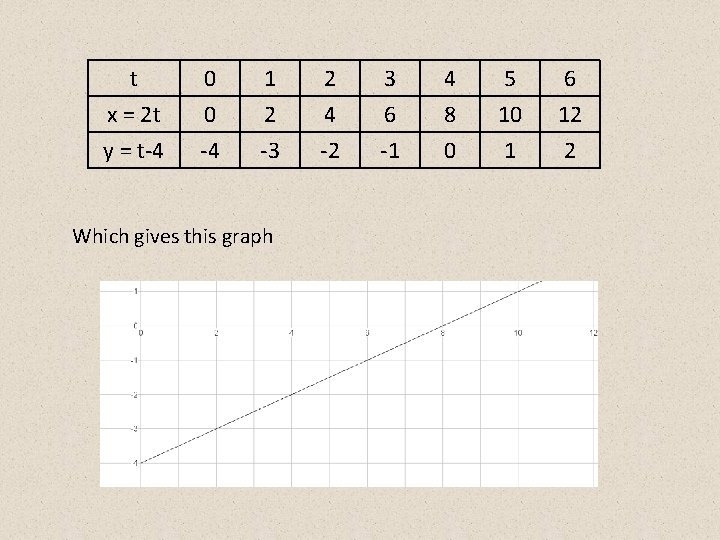
2. 1 You can define the coordinates of a point on a curve using parametric equations. In parametric equations, coordinates x and y are expressed as x = f(t) and y = g(t), where the variable t is a parameter. Sweet little things, they involve a three way relationship with x, y and t. Something like x = 2 t and y = t - 4 for 0 ≤ t ≤ 6 So you pop the values for t into the equations for x and y to give you some coordinates to plot.

t x = 2 t y = t-4 0 0 -4 1 2 -3 Which gives this graph 2 4 -2 3 6 -1 4 8 0 5 10 1 6 12 2

Exercise 2 A page 12

2. 2 You need to be able to use parametric equations to solve problems in coordinate geometry The first problem is when a curve meets the X or Y axis and you need to find the coordinates of the intersection Lets imagine the curve with parametric equations x = t², y = (1 -t)(t+3) meets the x axis when y = 0 then t = 1 giving x = 1 or t = -3 so x = 9 the coordinates of the intersections are (1, 0) and (9, 0)


The second problem occurs when one of the parametric equations has an unknown in it you need to find. a curve has parametric equations x = at², y = a(8 t³- 1) and passes through the point (4, 0). Find the value of a. using this value of t gives a = 16

The third type of problem occurs when a line and a curve meet and you need to find the point of intersection. The line x + y = 9 meets the curve with parametric equations x = t², y= (t+3)(t-2) at points P and Q. Find the coordinates of P and Q
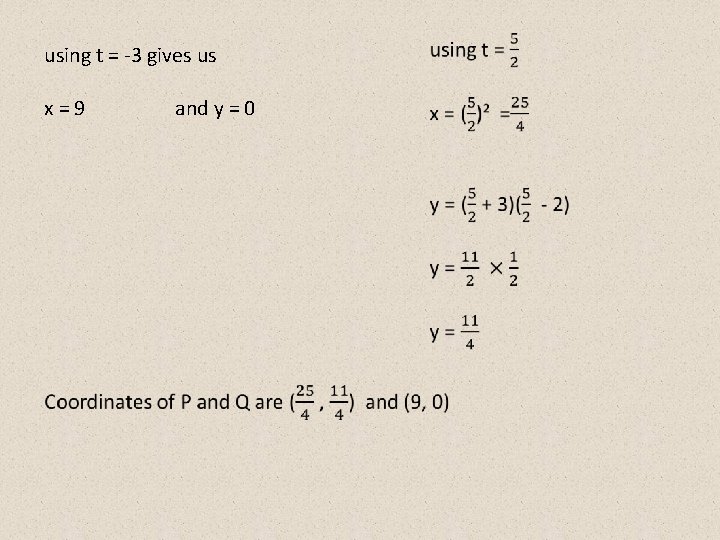
using t = -3 gives us x = 9 and y = 0

2. 3 You need to be able to convert parametric equations into a Cartesian equation You can find the Cartesian equation by eliminating the t

Let’s find the Cartesian equation of the ellipse we looked at earlier x = 2 – 4 cosϴ, y = 3 sinϴ + 4, 0 ≤ ϴ ≤ 2Π now we combine these two results using cos²ϴ + sin²ϴ = 1

exercise 2 C page 17

2. 4 You need to be able to find the area under a curve given by parametric equations

lets find the area of the finite region enclosed by the loop of the curve with parametric equations x = t² - 1 , y = ½(t – t)³ -2 ≤ t ≤ 2 limits for integration when x = 0 t = ± 1 this gives us turning to the next slide we see

exercise 2 D page 20
 Xy plane definition
Xy plane definition Coordinate geometry in the (x y) plane
Coordinate geometry in the (x y) plane Coordinate geometry in the (x y) plane
Coordinate geometry in the (x y) plane Coordinate geometry in the (x y) plane
Coordinate geometry in the (x y) plane Data plane control plane and management plane
Data plane control plane and management plane After me after me after me
After me after me after me If anyone desires to come after me
If anyone desires to come after me Coordinate bond of co
Coordinate bond of co What is pre coordinate indexing system
What is pre coordinate indexing system Coordinate geometry practice questions
Coordinate geometry practice questions Coordinate grid vocabulary
Coordinate grid vocabulary Length formula coordinate geometry
Length formula coordinate geometry Analytical geometry formulas
Analytical geometry formulas Coordinate geometry
Coordinate geometry Coordinate geometry gcse
Coordinate geometry gcse How to prove a parallelogram in coordinate geometry
How to prove a parallelogram in coordinate geometry Coordinate geometry proofs
Coordinate geometry proofs