CONVECTIVE FLUX FLUID MASS CONSERVATION The flux of

CONVECTIVE FLUX, FLUID MASS CONSERVATION The flux of any quantity in any direction is the rate per unit time per unit area that the quantity crosses a face normal to that direction. Quantities that can be fluxed in fluids include fluid mass, mass of a dissolved contaminant such as salt, mass of a suspended contaminant such as sediment, fluid momentum, fluid energy, heat, etc. There are three fundamental mechanisms of flux of interest in fluid mechanics: Convective flux, by which the quantity is carried with the flow; Diffusive flux, by which the quantity migrates from zones of high concentration to zones of low concentration by random molecular motion, and Radiative flux, by which the quantity (e. g. heat) is carried by waves such as electromagnetic waves (in the infrared spectrum in the case of heat). Here we are concerned only with the first two kinds. 1

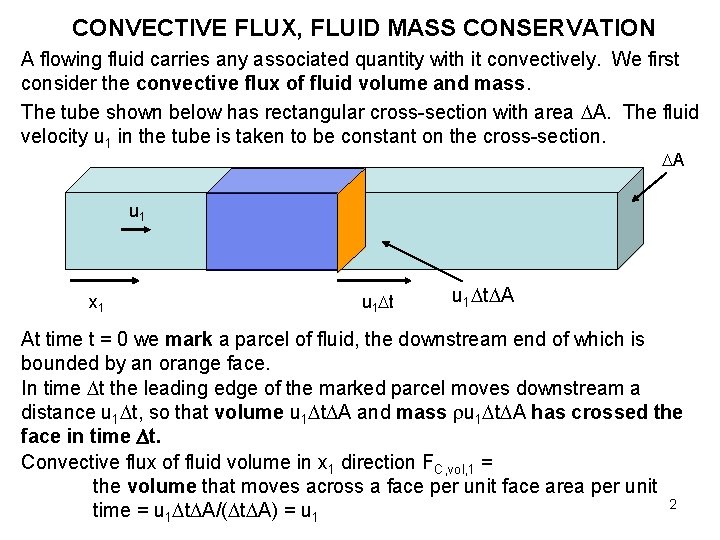
CONVECTIVE FLUX, FLUID MASS CONSERVATION A flowing fluid carries any associated quantity with it convectively. We first consider the convective flux of fluid volume and mass. The tube shown below has rectangular cross-section with area A. The fluid velocity u 1 in the tube is taken to be constant on the cross-section. A u 1 x 1 u 1 t A At time t = 0 we mark a parcel of fluid, the downstream end of which is bounded by an orange face. In time t the leading edge of the marked parcel moves downstream a distance u 1 t, so that volume u 1 t A and mass u 1 t A has crossed the face in time t. Convective flux of fluid volume in x 1 direction FC, vol, 1 = the volume that moves across a face per unit face area per unit 2 time = u 1 t A/( t A) = u 1

CONVECTIVE FLUX, FLUID MASS CONSERVATION The mass that crosses normal to the section in time t is density x volume crossed = u 1 t A The convective mass flux in the x 1 direction across the section = u 1 t A/( t A) = u 1. A u 1 x 1 u 1 t A The heat in a fluid is characterized by the heat capacity cp = heat needed to raise one kg of the fluid 1 degree. In the SI system, [cp] = joules/kg/°K. Where denotes the temperature of the fluid in °K, then, the amount of heat per unit volume in the fluid is cp ~ joules/m 3. The convective flux of heat in the x 1 direction = FC, heat, 1 heat that moves across a face per unit face area per unit time = cp u 1 t A/( t A) = cp u 1 3

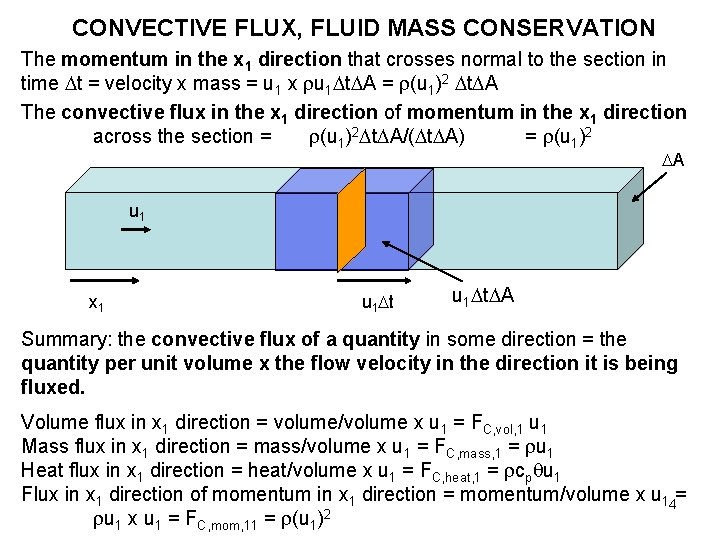
CONVECTIVE FLUX, FLUID MASS CONSERVATION The momentum in the x 1 direction that crosses normal to the section in time t = velocity x mass = u 1 x u 1 t A = (u 1)2 t A The convective flux in the x 1 direction of momentum in the x 1 direction across the section = (u 1)2 t A/( t A) = (u 1)2 A u 1 x 1 u 1 t A Summary: the convective flux of a quantity in some direction = the quantity per unit volume x the flow velocity in the direction it is being fluxed. Volume flux in x 1 direction = volume/volume x u 1 = FC, vol, 1 u 1 Mass flux in x 1 direction = mass/volume x u 1 = FC, mass, 1 = u 1 Heat flux in x 1 direction = heat/volume x u 1 = FC, heat, 1 = cp u 1 Flux in x 1 direction of momentum in x 1 direction = momentum/volume x u 14= u 1 x u 1 = FC, mom, 11 = (u 1)2

CONVECTIVE FLUX, FLUID MASS CONSERVATION A scalar quantity such as volume, mass and heat can be fluxed threedimensional space (x 1, x 2, x 3), so that the flux of a scalar quantity is a vector. The vectorial convective flux of a scalar quantity = the quantity per unit volume x the velocity vector. Thus the flux vectors of volume, fluid mass and heat are: FC, vol, i = ui, FC, mass, i = ui and FC, heat, i = cp ui. The flux of a scalar quantity across a face of specified direction ni is a scalar quantity, given as the dot produce of the flux vector and the unit normal of the face. Consider the illustrated face directed in the ni direction. The flux of fluid mass across the face is given as uini, i. e uini i. e. the component of the vector uini that is oriented normal to the face (and thus crosses it). In the diagram, the pink vector denotes ni, the red vector denotes uini, the blue vector denotes the component of uini that is parallel to the face (and thus does not cross it) and the green vector denotes the component uini of ui that is perpendicular to the face and thus is the mass flux across it. ui ni 5

CONVECTIVE FLUX, FLUID MASS CONSERVATION Let Fi denote the flux vector of some quantity and ni denote the unit normal vector of a face of area A. The discharge of the quantity across the face Qquan is a scalar given as The discharges of volume, mass and heat across the face are thus given as Note that no subscript is used in the case of volume discharge uini If ui is oriented normal to the face and has the value U which is constant across the face, the (volume) discharge is given as ui ni 6

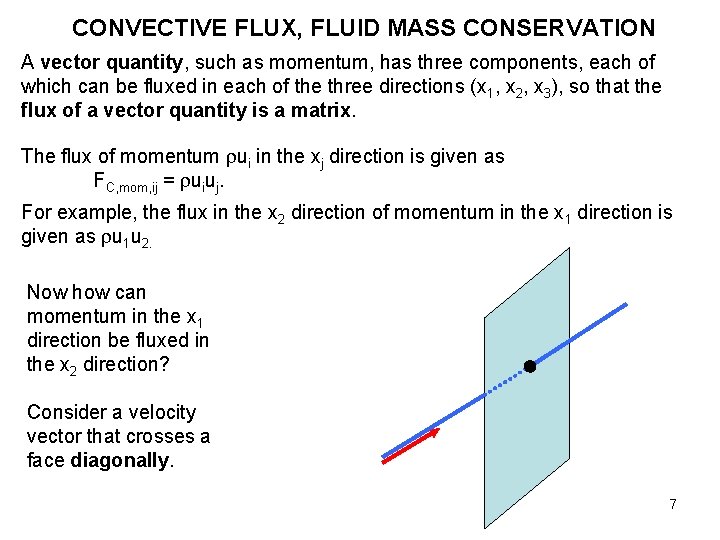
CONVECTIVE FLUX, FLUID MASS CONSERVATION A vector quantity, such as momentum, has three components, each of which can be fluxed in each of the three directions (x 1, x 2, x 3), so that the flux of a vector quantity is a matrix. The flux of momentum ui in the xj direction is given as FC, mom, ij = uiuj. For example, the flux in the x 2 direction of momentum in the x 1 direction is given as u 1 u 2. Now how can momentum in the x 1 direction be fluxed in the x 2 direction? Consider a velocity vector that crosses a face diagonally. 7

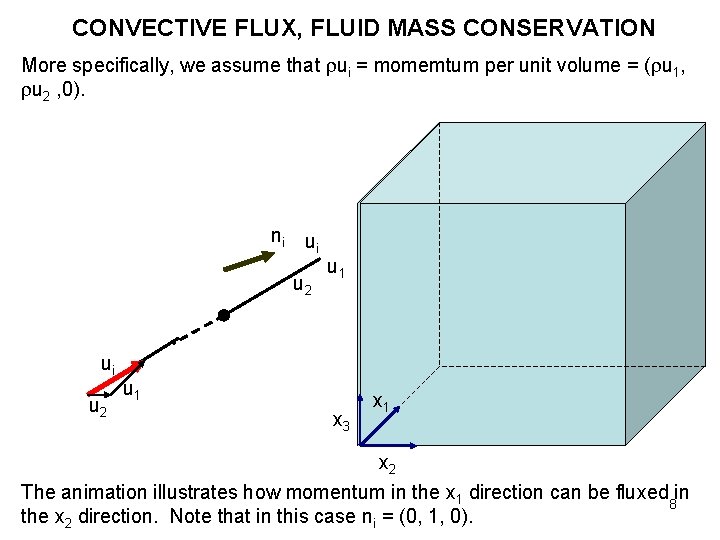
CONVECTIVE FLUX, FLUID MASS CONSERVATION More specifically, we assume that ui = momemtum per unit volume = ( u 1, u 2 , 0). ni u 2 ui u 2 u 1 x 3 x 1 x 2 The animation illustrates how momentum in the x 1 direction can be fluxed in 8 the x 2 direction. Note that in this case ni = (0, 1, 0).

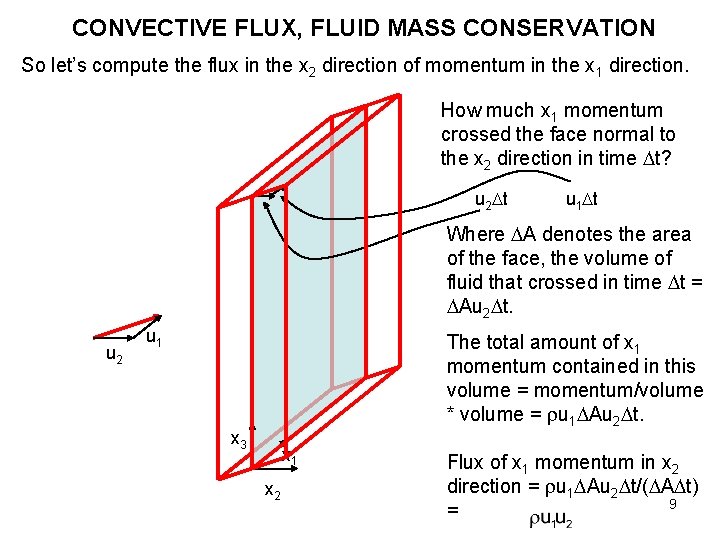
CONVECTIVE FLUX, FLUID MASS CONSERVATION So let’s compute the flux in the x 2 direction of momentum in the x 1 direction. How much x 1 momentum crossed the face normal to the x 2 direction in time t? u 2 t u 1 t Where A denotes the area of the face, the volume of fluid that crossed in time t = Au 2 t. u 2 u 1 The total amount of x 1 momentum contained in this volume = momentum/volume * volume = u 1 Au 2 t. x 3 x 1 x 2 Flux of x 1 momentum in x 2 direction = u 1 Au 2 t/( A t) 9 =

CONVECTIVE FLUX, FLUID MASS CONSERVATION The flux uiuj of momentum in the i direction across a face in the nj direction is a vector given as where ujnj denotes the component of the velocity that is actually normal to the face. Let nj denote a unit outward normal to a control volume that is fixed in space (so that fluid can flow in and out). The net inflow rate of the scalar quantity fluid mass into the control volume is ni d. A The net inflow rate Qmom, inflow, i of the vector quantity fluid momentum into the control volume is 10

CONVECTIVE FLUX, FLUID MASS CONSERVATION Equation of fluid mass conservation: / t(fluid mass in control volume) = net inflow rate of mass Now the control volume is fixed in space, so the equation can be rewritten as: But ni d. A So 11

CONVECTIVE FLUX, FLUID MASS CONSERVATION Now the condition must be true for any volume V. The only way this can hold is if the integrand vanishes everywhere: The above equation is the equation of mass conservation, or continuity equation of a fluid. ni d. A For an incompressible fluid, i. e. one for which can be locally approximated as constant, the relation reduces to 12

CONVECTIVE FLUX, FLUID MASS CONSERVATION But this result is predicated on the following theorem: , if A = A(xi) is a continuous function of xi and simply-connected volume in a given domain, then everywhere within that domain. The equivalent 1 D theorem can be stated as follows. Let f(x) be a continuous function such that for every set of values x 1 and x 2 within a given domain Then everywhere within that domain 13

CONVECTIVE FLUX, FLUID MASS CONSERVATION Proof: if everywhere within some domain, then where x is a free variable within that domain, Now take the derivative with respect to x to obtain and the desired result is proved. 14

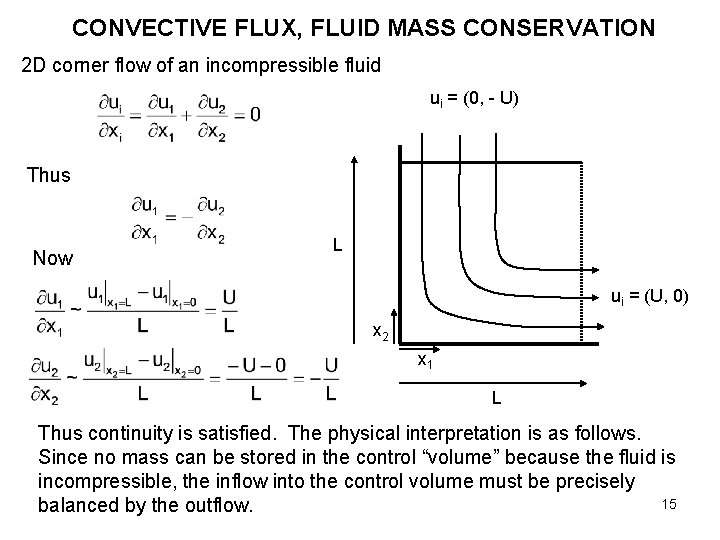
CONVECTIVE FLUX, FLUID MASS CONSERVATION 2 D corner flow of an incompressible fluid ui = (0, - U) Thus Now L ui = (U, 0) x 2 x 1 L Thus continuity is satisfied. The physical interpretation is as follows. Since no mass can be stored in the control “volume” because the fluid is incompressible, the inflow into the control volume must be precisely 15 balanced by the outflow.