Computational Logic Lecture 2 Propositional Logic Michael Genesereth

Computational Logic Lecture 2 Propositional Logic Michael Genesereth Autumn 2009

Complexity The cherry blossoms in the spring … sank. 1/22/2022 2

Ambiguity Leland Stanford Junior University Leland-Stanford Junior-University? Leland-Stanford-Junior 1/22/2022 University? 3

Ambiguity There’s a girl in the room with a telescope. 1/22/2022 4

Ambiguity Lettuce won’t turn brown if you put your head in a plastic bag before placing it in the refrigerator. The manager of a nudist colony complains that a hole was cut in the wall surrounding the camp. Police are looking into it. 1/22/2022 5

Ambiguity - Headlines Crowds Rushing to See Pope Trample 6 to Death Tips to Help You Prevent Headaches After You Die Bundy Beats Date With Chair Police Oversight Group Likes San Jose Model Japanese Scientists Grow Frog Eyes and Ears Food Stamp Recipients Turn to Plastic Indian Ocean Talks 1/22/2022 6

Meaning not Syntax Champagne is better than soda. Soda is better than swill. Therefore, champagne is better than swill. Bad sex is better than nothing. Nothing is better than good sex. Therefore, bad sex is better than good sex. 1/22/2022 7

Propositional Languages A propositional signature is a set/sequence of primitive symbols, called proposition constants. Given a propositional signature, a propositional sentence is either (1) a member of the signature or (2) a compound expression formed from members of the signature. (Details to follow. ) A propositional language is the set of all propositional sentences that can be formed from a propositional signature. 1/22/2022 8

Proposition Constants By convention (in this course), proposition constants are written as strings of alphanumeric characters beginning with a lower case letter. Examples: raining r 32 aining r. Ai. Ng rainingorsnowing Non-Examples: 324567 raining. or. snowing 1/22/2022 9

Compound Sentences Negations: raining The argument of a negation is called the target. Conjunctions: (raining snowing) The arguments of a conjunction are called conjuncts. Disjunctions: (raining snowing) The arguments of a disjunction are called disjuncts. 1/22/2022 10

Compound Sentences (concluded) Implications: (raining cloudy) The left argument of an implication is the antecedent. The right argument is the consequent. Reductions: (cloudy raining) The left argument of a reduction is the consequent. The right argument of a reduction is the antecedent. Equivalences: 1/22/2022 (cloudy raining) 11

Parenthesis Removal Dropping Parentheses is good: (p q) p q But it can lead to ambiguities: ((p q) r) p q r (p (q r)) p q r 1/22/2022 12

Precedence Parentheses can be dropped when the structure of an expression can be determined by precedence. NB: An operand associates with operator of higher precedence. If surrounded by operators of equal precedence, the operand associates with the operator to the right. p q r p q p q r 1/22/2022 13

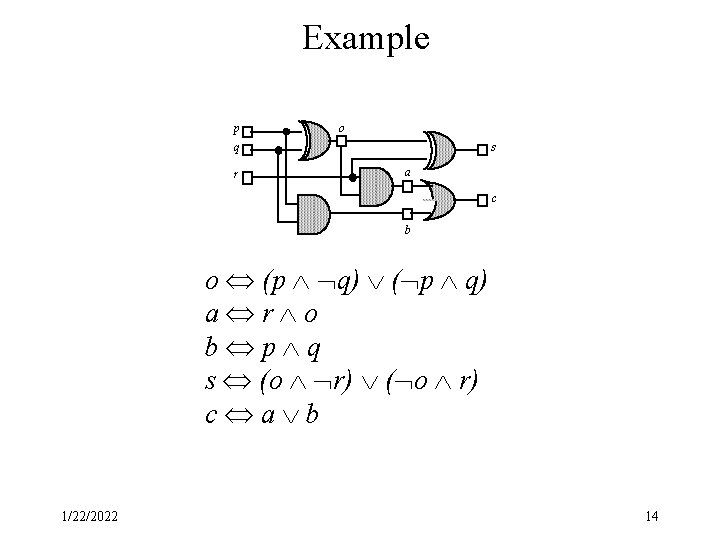
Example p o q r s a c b o (p q) ( p q) a r o b p q s (o r) ( o r) c a b 1/22/2022 14

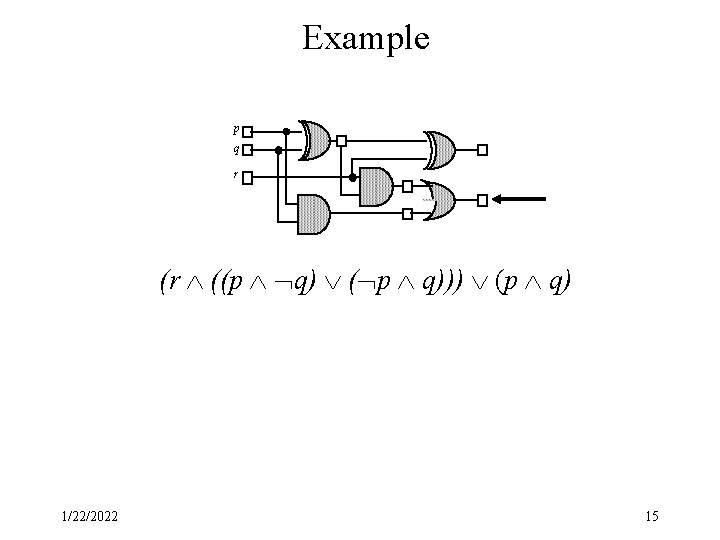
Example p q r (r ((p q) ( p q))) (p q) 1/22/2022 15

Propositional Interpretation A propositional interpretation is an association between the propositional constants in a propositional language and the truth values T or F. We sometimes view an interpretation as a Boolean vector of values for the items in the signature of the language (when the signature is ordered). i = TFT 1/22/2022 16

Sentential Interpretation A sentential interpretation is an association between the sentences in a propositional language and the truth values T or F. pi = T qi = F ri = T (p q)i = T ( q r)i = T ((p q) ( q r))i = T A propositional interpretation defines a sentential interpretation by application of operator semantics. 1/22/2022 17

Operator Semantics Negation: For example, if the interpretation of p is F, then the interpretation of p is T. For example, if the interpretation of (p q) is T, then the interpretation of (p q) is F. 1/22/2022 18

Operator Semantics (continued) Conjunction: Disjunction: NB: The type of disjunction here is called inclusive or, which says that a disjunction is true if and only if at least one of its disjuncts is true. This contrasts with exclusive or, which says that a disjunction is true if and only if an odd number of its disjuncts is true. 1/22/2022 19

Operator Semantics (continued) Implication: Reduction: NB: The semantics of implication here is called material implication. Any implication is true if the antecedent is false, whether or not there is a connection to the consequent. If George Washington is alive, I am a billionaire. 1/22/2022 20

Operator Semantics (concluded) Equivalence: 1/22/2022 21

Evaluation Interpretation i: Compound Sentence (p q) ( q r) 1/22/2022 22

Example pi = T qi = T ri = T p q r (r ((p q) ( p q))) (p q) 1/22/2022 23

Multiple Interpretations Logic does not prescribe which interpretation is “correct”. In the absence of additional information, one interpretation is as good as another. Interpretation i Interpretation j Examples: Different days of the week Different locations Beliefs of different people 1/22/2022 24

Truth Tables A truth table is a table of all possible interpretations for the propositional constants in a language. One column per constant. One row per interpretation. For a language with n constants, there are 2 n interpretations. 1/22/2022 25

Properties of Sentences Valid Contingent Unsatisfiable 1/22/2022 A sentence is valid if and only if every interpretation satisfies it. A sentence is contingent if and only if some interpretation satisfies it and some interpretation falsifies it. A sentence is unsatisfiable if and only if no interpretation satisfies it. 26

Properties of Sentences Valid A sentences is satisfiable if and only if it is either valid or contingent. A sentences is falsifiable if and only if it is contingent or unsatisfiable. Contingent Unsatisfiable 1/22/2022 27

Example of Validity 1/22/2022 28

More Validities Double Negation: p p de. Morgan's Laws: (p q) ( p q) Implication Introduction: p (q p) Implication Distribution (p (q r)) ((p q) (p r)) 1/22/2022 29

Evaluation Versus Satisfaction Evaluation: Satisfaction: 1/22/2022 30

Example pi = ? qi = ? ri = ? p q r ((r ((p q) ( p q))) (p q))i = T 1/22/2022 31

Satisfaction Method to find all propositional interpretations that satisfy a given set of sentences: (1) Form a truth table for the propositional constants. (2) For each sentence in the set and each row in the truth table, check whether the row satisfies the sentence. If not, cross out the row. (3) Any row remaining satisfies all sentences in the set. (Note that there might be more than one. ) 1/22/2022 32

Satisfaction Example q r 1/22/2022 33

Satisfaction Example (continued) q r p q r 1/22/2022 34

Satisfaction Example (concluded) q r p q r r 1/22/2022 35

Axiomatizability A set of boolean vectors of length n is axiomatizable in propositional logic if and only if there is a signature of size n and a set of sentences from the corresponding language such that the vectors in the set correspond to the set of interpretations satisfying the sentences. A set of sentences defining a set of vectors is called the axiomatization of the set of vectors. 1/22/2022 36

Example Set of bit vectors: {TFF, FTT} Signature: {p, q, r} Axiomatization: (p q r) ( p q) 1/22/2022 37

The Big Game Stanford people always tell the truth, and Berkeley people always lie. Unfortunately, by looking at a person, you cannot tell whether he is from Stanford or Berkeley. You come to a fork in the road and want to get to the football stadium down one fork. However, you do not know which to take. There is a person standing there. What single question can you ask him to help you decide which fork to take? 1/22/2022 38

Basic Idea 1/22/2022 39

The Big Game Solved Question: The left road the way to the stadium if and only if you are from Stanford. Is that correct? 1/22/2022 40