Introduction to Logic Propositional Analysis Michael Genesereth Computer

Introduction to Logic Propositional Analysis Michael Genesereth Computer Science Department Stanford University

Programme Properties of Sentences Validity, Contingency, Unsatisfiability Satisfiability and Falsifiability Relationships between Sentences Equivalence, Entailment, Consistency Theorems connecting these Properties and Relationships Equivalence Theorem Unsatisfiability Theorem Deduction Theorem Consistency Theorem

Properties of Sentences

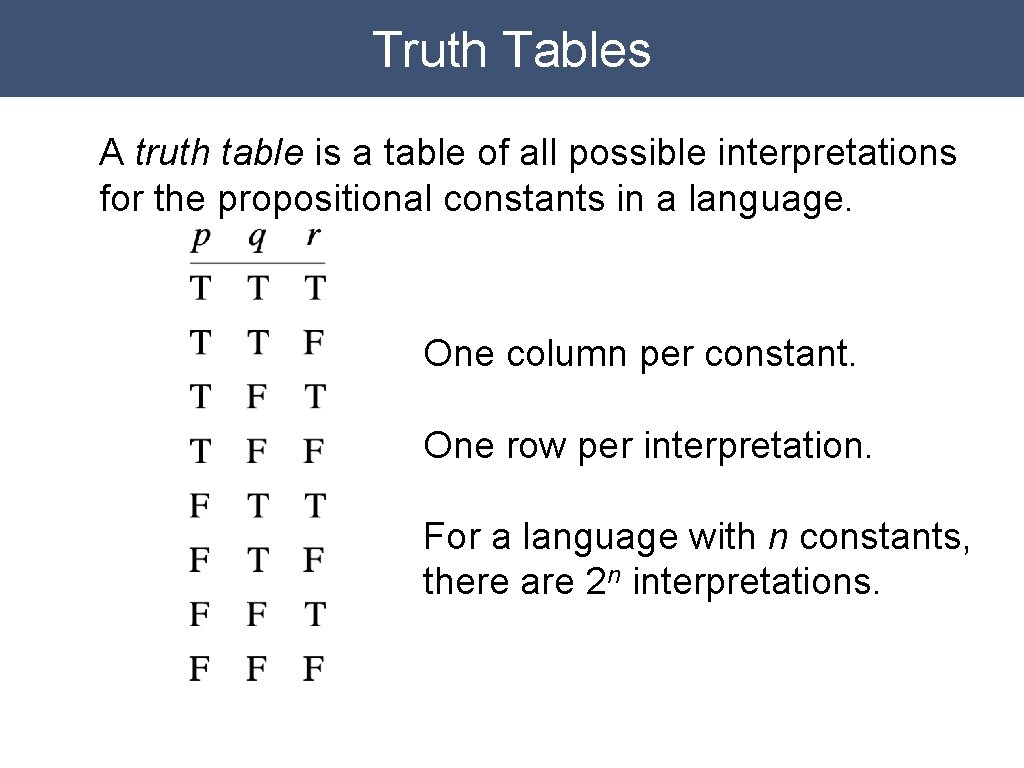
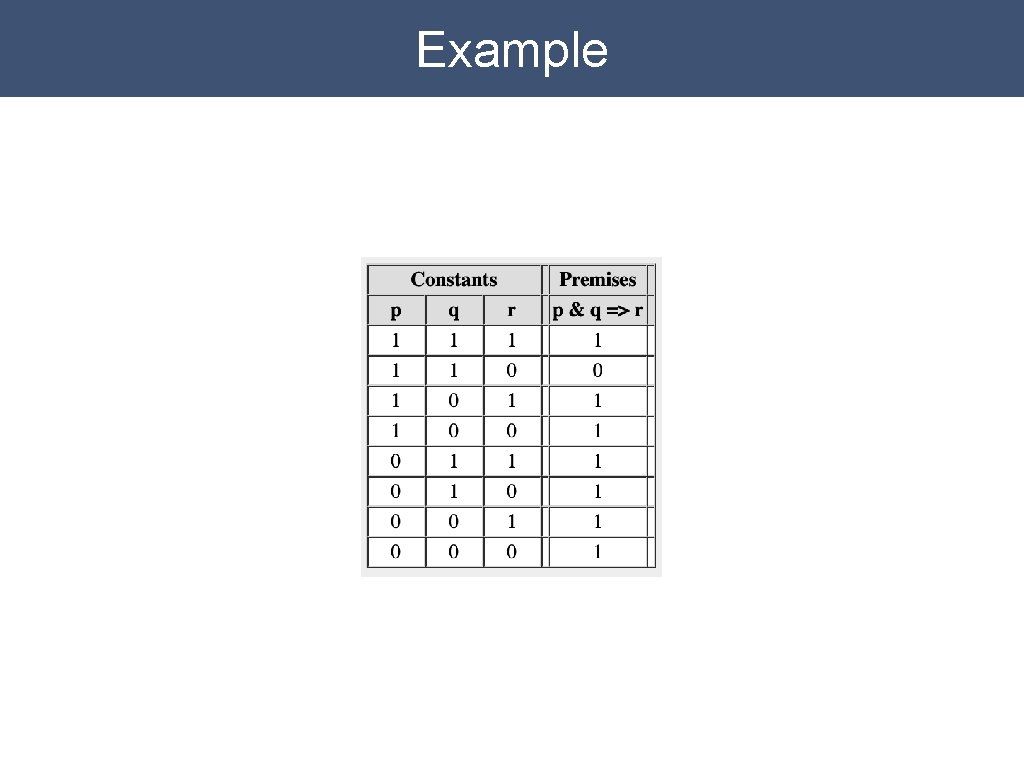
Truth Tables A truth table is a table of all possible interpretations for the propositional constants in a language. One column per constant. One row per interpretation. For a language with n constants, there are 2 n interpretations.

Example

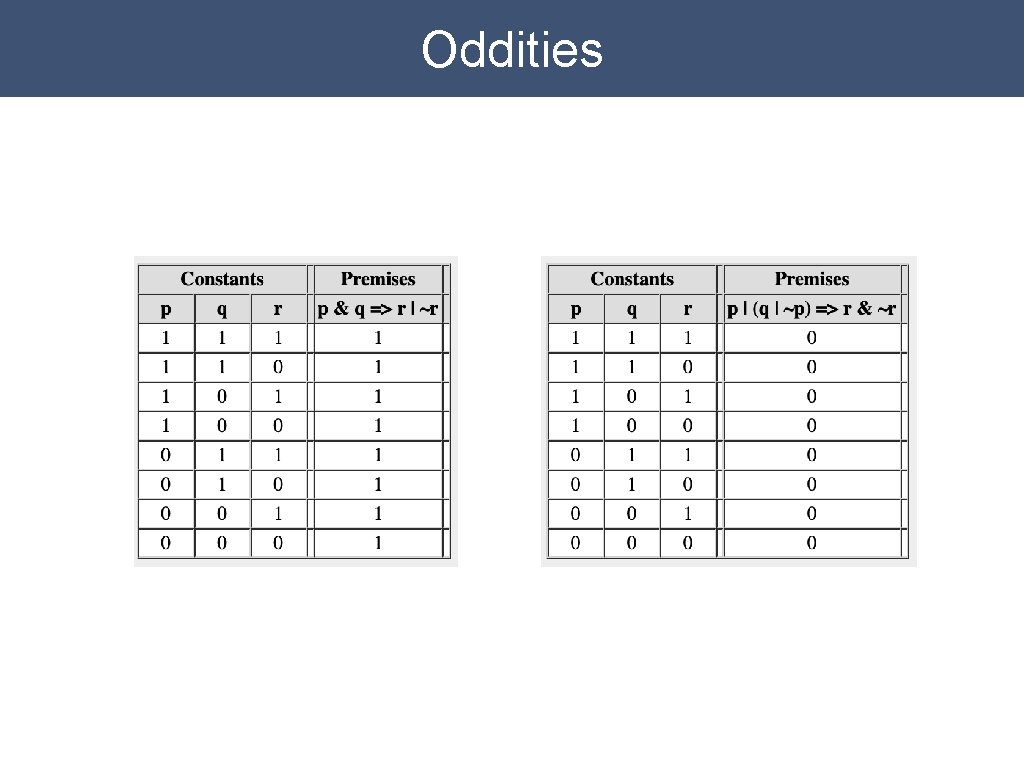
Oddities

Properties of Sentences Valid Contingent Unsatisfiable A sentence is valid if and only if every interpretation satisfies it. A sentence is contingent if and only if some interpretation satisfies it and some interpretation falsifies it. A sentence is unsatisfiable if and only if no interpretation satisfies it.

Properties of Sentences Valid } A sentences is satisfiable if and only if it is either valid or contingent. } A sentences is falsifiable if and only if it is contingent or unsatisfiable. Contingent Unsatisfiable

Possible Worlds

Possible Worlds

Possible Worlds

Possible Worlds

Valid Equivalences Double Negation: p Û ØØp de. Morgan's Laws: Ø(pÙq) Û (ØpÚØq) Ø(pÚq) Û (ØpÙØq)

Valid Implications Implication Introduction: p Þ (q Þ p) Implication Distribution (p Þ (q Þ r)) Þ ((p Þ q) Þ (p Þ r)) Implication Reversal (Øq Þ Øp) Þ (p Þ q)

Properties of Sentences

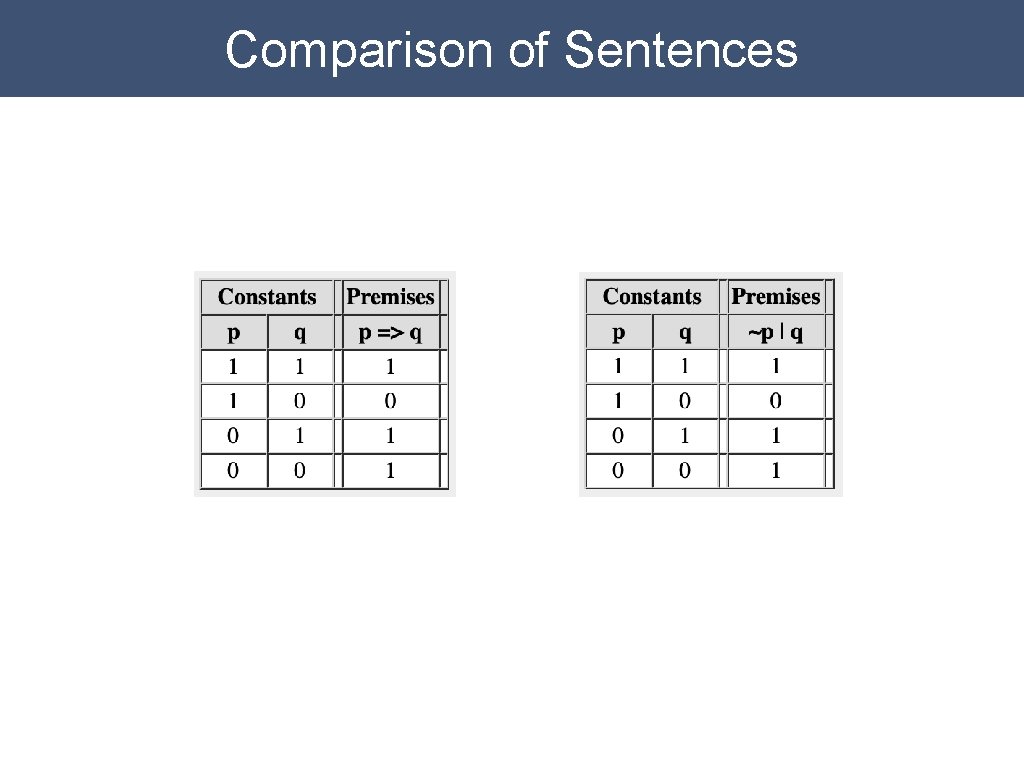
Comparison of Sentences

Logical Equivalence A sentence φ is logically equivalent to a sentence ψ if and only if every truth assignment that satisfies φ satisfies ψ and every truth assignment that satisfies ψ satisfies φ. (p Þ q) is logically equivalent to (Øp Ú q) p is logically equivalent to ØØp (p Ù q) is not logically equivalent to (p Ú q)

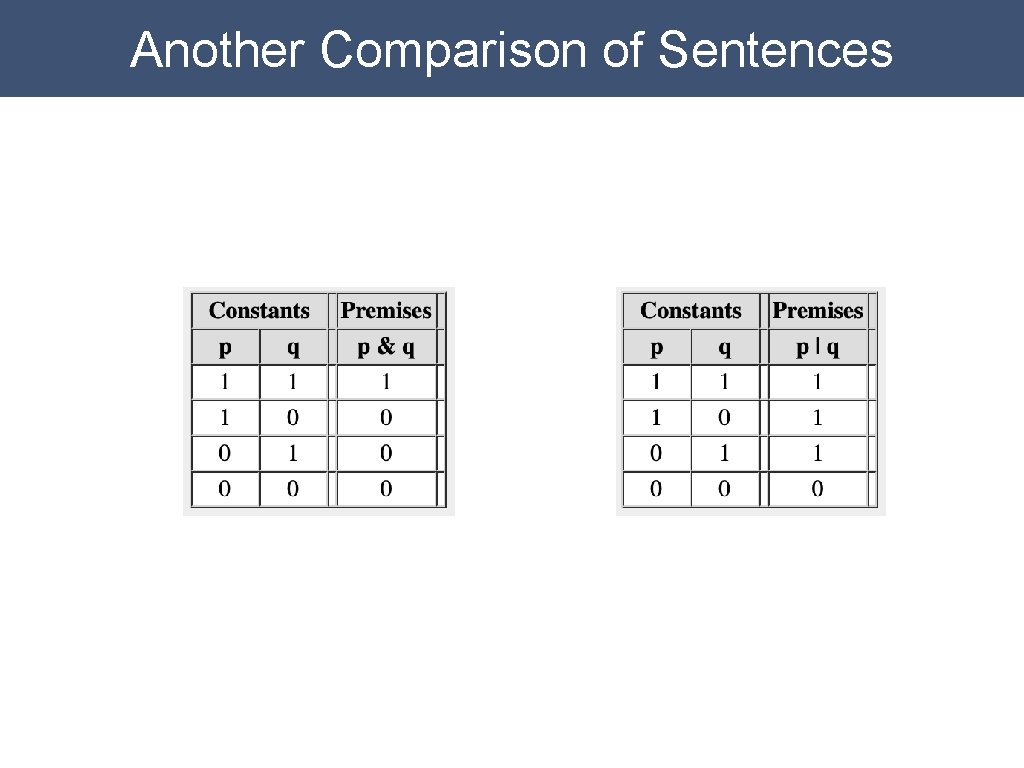
Another Comparison of Sentences

Logical Entailment A premise j logically entails a conclusion y (written as j ⊨ y) if and only if every interpretation that satisfies j also satisfies y. (p Ù q) ⊨ (p Ú q) p ⊨ (p Ú q) (p Ù q) ⊨ p p ⊭ (p Ù q)

Logical Entailment ¹ Logical Equivalence p ⊨ (p Ú q) ⊭ p Analogy in arithmetic: inequalities rather than equations

Sets of Premises A set of premises D logically entails a conclusion j (written as D ⊨ j) if and only if every interpretation that satisfies all of the premises also satisfies the conclusion. {p, q} ⊨ (p Ù q)

Sets of Conclusions A premise j logically entails a set of conclusions if and only if every interpretation that satisfies the premise satisfies all of the conclusions. (p Ù q) ⊨ {p, q}

Truth Table Method We can check for logical entailment by comparing tables of all possible interpretations. In the first table, eliminate all rows that do not satisfy premises. In the second table, eliminate all rows that do not satisfy the conclusion. If the remaining rows in the first table are a subset of the remaining rows in the second table, then the premises logically entail the conclusion.

Example If Mary loves Pat, then Mary loves Quincy. If it is Monday, then Mary loves Pat or Quincy. If it is Monday, does Mary love Quincy? m p q T T T ´ ´ ´ T F T ´ ´ ´ F T F F T F F F

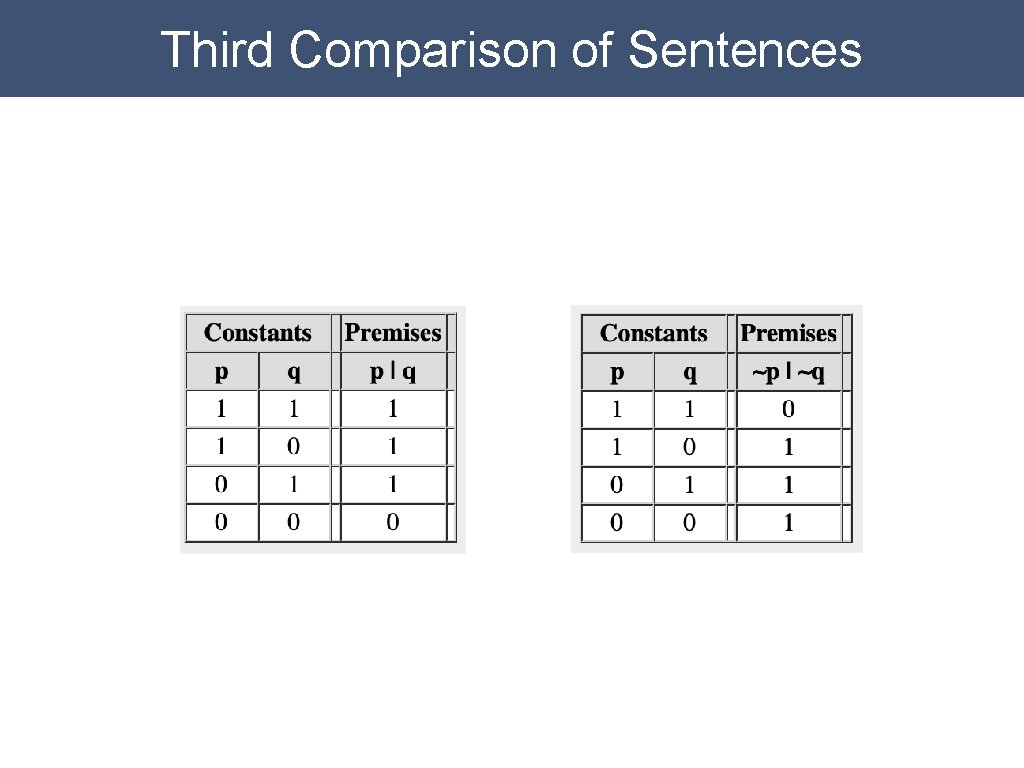
Third Comparison of Sentences

Logical Consistency A sentence φ is consistent with a sentence ψ if and only if there is a truth assignment that satisfies both φ and ψ. p is logically consistent with q (p Ú q) is logically consistent with (Øp Ú Øq) (p Þ q) is logically consistent with (Øp Ú q) p is not consistent with Øp

Connections

Equivalence Theorem: A sentence φ and a sentence ψ are logically equivalent if and only if the sentence (φ ⇔ ψ) is valid. Is Ø(pÙq) logically equivalent to (ØpÚØq)? Is (Ø(pÙq) Û (ØpÚØq)) valid? Upshot: We can determine equivalence of sentences by checking validity of a single sentence.

Unsatisfiability Theorem: D ⊨ j if and only if D È {Øj} is unsatisfiable. Proof: Suppose that D ⊨ j. If an interpretation satisfies D, then it must also satisfy j. But then it cannot satisfy Øj. Therefore, D È {Øj} is unsatisfiable. Suppose that D È {Øj} is unsatisfiable. Then every interpretation that satisfies D must fail to satisfy Øj, i. e. it must satisfy j. Therefore, D ⊨ j. Upshot: We can determine logical entailment between sentences by checking unsatisfiability of a single sentence.

Example {(pÞq), (m Þ pÚq)} ⊨ (mÞq)? Is {(pÞq), (m Þ pÚq), Ø(mÞq)} unsatisfiable? m p q T T T F F F T T F F F

Deduction Theorem: A sentence φ logically entails a sentence ψ if and only if (φ ⇒ ψ) is valid. More generally, a finite set of sentences {φ , . . . , φ} logically entails φ if and only if the compound sentence (φ ∧. . . ∧ ⇒ φ φ) is valid. 1 1 n {(pÞq), (m Þ pÚq)} ⊨ (mÞq)? Is ((pÞq) ∧ (m Þ pÚq) Þ (mÞq)) valid? Upshot: We can determine logical entailment between sentences by checking validity of a single sentence.

Consistency Theorem: A sentence φ is logically consistent with a sentence ψ if and only if the sentence (φ ∧ ψ) is satisfiable. More generally, a sentence φ is logically consistent with a finite set of sentences {φ1, . . . , φn} if and only if the compound sentence (φ1 ∧. . . ∧n ∧ φ φ) is satisfiable. Is (pÚq) consistent with (ØpÚØq)? Is ((pÚq) Ù (ØpÚØq)) satisfiable? Upshot: We can determine consistency of sentences by checking satisfiability of a single sentence.