Clustering In Large Graphs And Matrices Petros Drineas

  • Slides: 17
Download presentation
Clustering In Large Graphs And Matrices Petros Drineas, Alan Frieze, Ravi Kannan, Santosh Vempala,

Clustering In Large Graphs And Matrices Petros Drineas, Alan Frieze, Ravi Kannan, Santosh Vempala, V. Vinay Presented by Eric Anderson

Outline Clustering: discrete vs. continuous ¢ Singular Value Decomposition (SVD) ¢ Applying SVD to

Outline Clustering: discrete vs. continuous ¢ Singular Value Decomposition (SVD) ¢ Applying SVD to clustering ¢ Algorithm ¢ Analysis and results ¢

Clustering ¢ Group m similar points in n, or equivalently, group similar rows of

Clustering ¢ Group m similar points in n, or equivalently, group similar rows of an m x n matrix A ¢ m, n considered variable, k fixed ¢ Many options for goals

Discrete Clustering (DCP) ¢ Minimizes sum of squared distances to k cluster centers: ¢

Discrete Clustering (DCP) ¢ Minimizes sum of squared distances to k cluster centers: ¢ Cluster centers are the centroids of the cluster points Each point belongs to one, and only one, cluster Slow Voronoi algorithm supplied: ¢ ¢

Continuous Clustering (CCP) ¢ Minimizes sum of squared distances nto some k-dimensional subspace V

Continuous Clustering (CCP) ¢ Minimizes sum of squared distances nto some k-dimensional subspace V of : ¢ Gives a lower bound on the optimal value of DCP, eg. V=span(B) Result: each point belongs to each cluster with some intensity Overlap is allowed, but now intensity vectors (of clusters) must be orthogonal ¢ ¢

CCP Continued ¢ ¢ ¢ " i, let xi be the ith cluster, an

CCP Continued ¢ ¢ ¢ " i, let xi be the ith cluster, an m-vector of intensities The weight of x is Require Optimal clustering of A is a set of orthonormal x 1, …, xk where xi is a maximum weight cluster of A subject to being orthogonal to x 1, …, xi-1 Orthogonality: xi. Txj=0 for i≠j

More CCP ¢ Orthogonality needed: let v=λu+w where u and w are orthogonal, u

More CCP ¢ Orthogonality needed: let v=λu+w where u and w are orthogonal, u is the maximum weight cluster. Then so λ should be 0 for v to be of maximum weight when u is removed

Approximating DCP with CCP Compute V from CCP ¢ Project A onto V and

Approximating DCP with CCP Compute V from CCP ¢ Project A onto V and solve DCP in k dimensions ¢ Result is shown to be a 2 approximation for full DCP (optimal value is off by a factor of no more than 2) ¢

Frobenius Norm ¢ Definition: Similar to 2 -norm for vectors ¢ Not the matrix

Frobenius Norm ¢ Definition: Similar to 2 -norm for vectors ¢ Not the matrix 2 -norm ¢

Singular Value Decomposition (SVD) ¢ The SVD of a matrix A is ¢ Singular

Singular Value Decomposition (SVD) ¢ The SVD of a matrix A is ¢ Singular values Singular vectors Frobenius norm: ¢ ¢

Use of SVD ¢ Minimizes error in rank k approximations: ¢ This solves CCP:

Use of SVD ¢ Minimizes error in rank k approximations: ¢ This solves CCP: where is the projection of A onto V, is minimized by Dk, since is of rank at most k.

Algorithm ¢ ¢ ¢ SVD is rather slow, especially for large matrices Choose random

Algorithm ¢ ¢ ¢ SVD is rather slow, especially for large matrices Choose random columns of A for SVD, forming A* Want to find columns so that with D* induced by the first k singular vectors of A*, for some ε>0.

Algorithm Continued ¢ Steps: 1. Choose c>0, ε>0, δ<1. Let s=4 k/(εcδ). For each

Algorithm Continued ¢ Steps: 1. Choose c>0, ε>0, δ<1. Let s=4 k/(εcδ). For each i, include column with probability , in matrix S. 2. Find STS. 3. Find the top k eigenvectors pi of STS, and for each I, return as the clusters.

Analysis of Algorithm ¢ It is shown that with probability at least 1 -

Analysis of Algorithm ¢ It is shown that with probability at least 1 - δ, ¢ In practice, can pick fewer columns Actual method: check error by randomly sampling elements of and repeat if not satisfactory Running time: O(k 3/ε 6+k 2 m/ε 4) ¢ ¢

Preliminary Results ¢ ¢ ¢ Generated 1000 x 1000 random matrices with certain singular

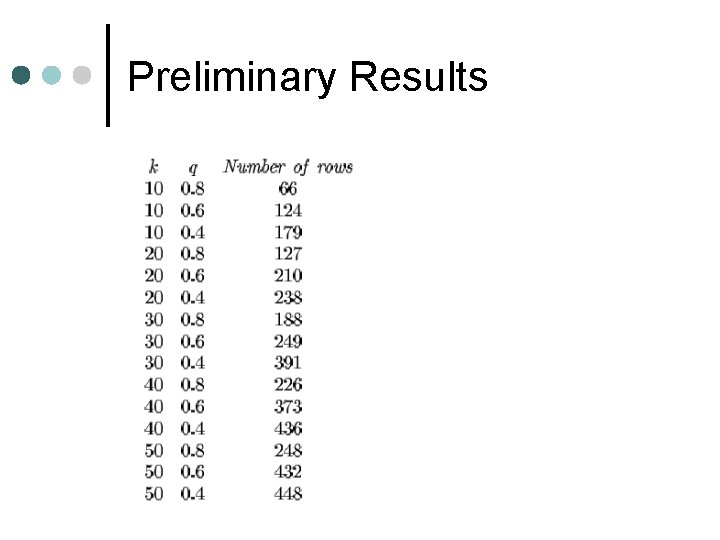
Preliminary Results ¢ ¢ ¢ Generated 1000 x 1000 random matrices with certain singular value distributions Distributions defined by q: fraction of Frobenius norm contained in first k singular values Checked number of columns of A necessary to get a 3% error bound (ε=0. 03)

Preliminary Results

Preliminary Results

Conclusion Useful new definition of clusters ¢ Good (linear in m) running time to

Conclusion Useful new definition of clusters ¢ Good (linear in m) running time to approximate CCP ¢ Forms 2 -approximation for DCP ¢ A new use for the SVD ¢

Rand NLA Randomized Numerical Linear Algebra Petros DrineasRand NLA Randomized Numerical Linear Algebra Petros Drineas
Matlab Tutorial Matrices Matrices Matrices Rows and columnsMatlab Tutorial Matrices Matrices Matrices Rows and columns
1 Matrices 1 Matrices 2 Tipos de matrices1 Matrices 1 Matrices 2 Tipos de matrices
Matrices 1 Tema 1 MATRICES Matrices 2 1Matrices 1 Tema 1 MATRICES Matrices 2 1
Captulo 7 Arreglos II Matrices Matrices Las matricesCaptulo 7 Arreglos II Matrices Matrices Las matrices
Matrices Addition of Matrices We add two matricesMatrices Addition of Matrices We add two matrices
MATRICES Matrices Las matrices son arreglos compuestos porMATRICES Matrices Las matrices son arreglos compuestos por
Lecture 12 Clustering What is Clustering Clustering isLecture 12 Clustering What is Clustering Clustering is
ENSEMBLE CLUSTERING ENSEMBLE CLUSTERING clustering algorithm 1 partitionENSEMBLE CLUSTERING ENSEMBLE CLUSTERING clustering algorithm 1 partition
FLAT CLUSTERING HIERARCHICAL CLUSTERING What is clustering GroupingFLAT CLUSTERING HIERARCHICAL CLUSTERING What is clustering Grouping
DATA MINING CLUSTERING Clustering 4 Clustering unsupervised classificationDATA MINING CLUSTERING Clustering 4 Clustering unsupervised classification
Clustering Kmeans Clustering 2 means Clustering Curve ShowsClustering Kmeans Clustering 2 means Clustering Curve Shows
Kmeans Clustering Kmeans Clustering What is clustering WhyKmeans Clustering Kmeans Clustering What is clustering Why
C 0 clustering Liang Zheng Clustering Clustering alongC 0 clustering Liang Zheng Clustering Clustering along
Variable Clustering 1 Variable Clustering Variable clustering findsVariable Clustering 1 Variable Clustering Variable clustering finds
CLUSTERING Overview Definition of Clustering Existing clustering methodsCLUSTERING Overview Definition of Clustering Existing clustering methods