C 0 clustering Liang Zheng Clustering Clustering along

C 0 -clustering Liang Zheng

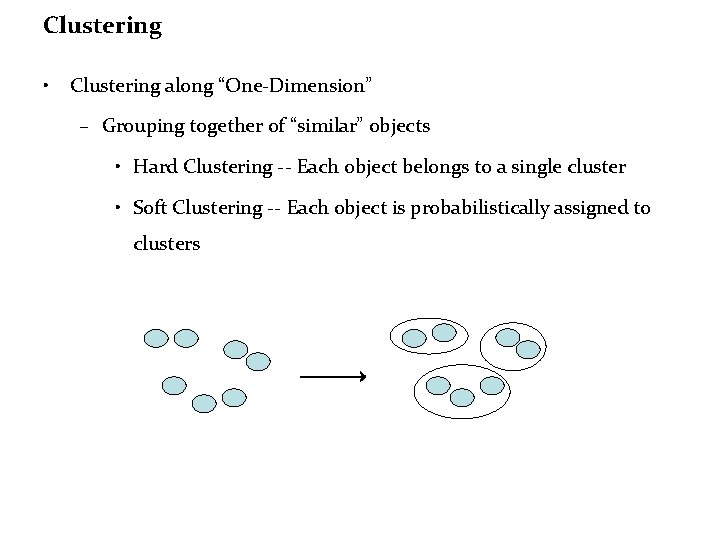
Clustering • Clustering along “One-Dimension” – Grouping together of “similar” objects • Hard Clustering -- Each object belongs to a single cluster • Soft Clustering -- Each object is probabilistically assigned to clusters

C 0 -clustering • Given a multi-dimensional data matrix, co-clustering refers to simultaneous clustering along multiple dimensions. Co-occurrence Matrices Characteristics • Data sparseness • High dimension • Noise Doc-Term Co-occurrence Matrix

Related Methods 1. • Information-Theoretic Co-Clustering (ITCC) • Graph-partitioning based Co-Clustering (GPCC) Dhillon I S, Mallela S, Modha D S. Information-theoretic co-clustering[C]//Proceedings of the ninth ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, 2003: 89 -98. 2. Dhillon I S. Co-clustering documents and words using bipartite spectral graph partitioning[C]//Proceedings of the seventh ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, 2001: 269 -274. Inderjit S. Dhillon Center for Big Data Analytics Department of Computer Science University of Texas at Austin

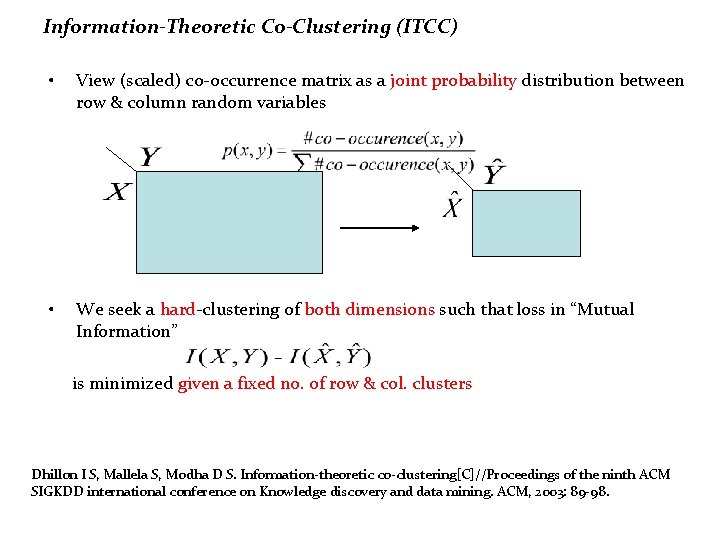
Information-Theoretic Co-Clustering (ITCC) • View (scaled) co-occurrence matrix as a joint probability distribution between row & column random variables • We seek a hard-clustering of both dimensions such that loss in “Mutual Information” is minimized given a fixed no. of row & col. clusters Dhillon I S, Mallela S, Modha D S. Information-theoretic co-clustering[C]//Proceedings of the ninth ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, 2003: 89 -98.

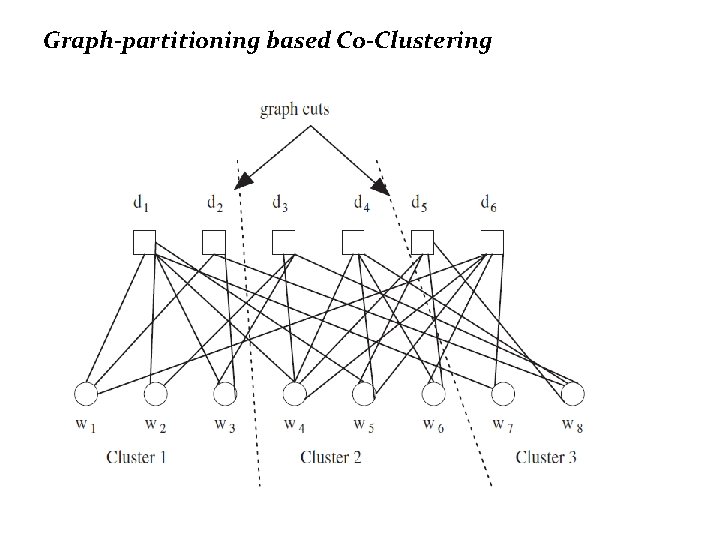
Graph-partitioning based Co-Clustering

• Given disjoint document clusters D 1, . . . , Dk, the corresponding word clusters W 1, . . . , Wk may be determined as follows. • A given word wi belongs to the word cluster Wm if its association with the document cluster Dm is greater than its association with any other document cluster. • A natural measure of the association of a word with a document cluster is the sum of the edge-weights to all documents in the cluster. • Clearly the “best” word and document clustering would correspond to a partitioning of the graph such that the crossing edges between partitions have minimum weight.

GPCC算法 • Adjacency Matrix Laplacian matrix • This problem can be tackled with an SVD-related algorithm. • O(|E| + h logh) h=m+n (L=D-A) D: degree matrix

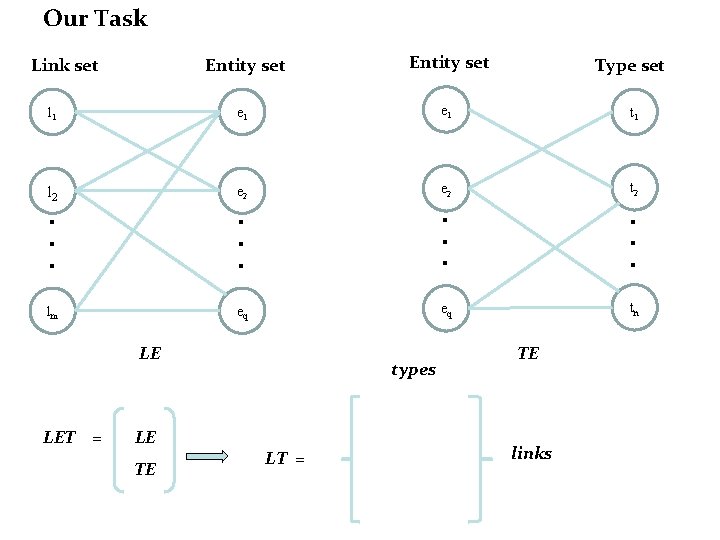
Our Task Entity set l 1 e 1 t 1 l 2 e 2 t 2 . . . lm eq eq tn Link set LE LET = LE TE types LT = Type set TE links

问题就可以描述为Link—Entity—Type协同聚类的问题： 给定Link set L、Entity set E、Type set T、整数k 和关联强度函数 Relevance, 由协同聚类得到一个集合C 且Cx = (Lx, Tx) (1≤x≤k) , 使得 li Lx , tj Ty Relevance (li , tj)最小. (x, y= 1, . . . , k且x y) Definition li: tx ; li关联到types tj: ly; tj关联到links Relevance(li , tj)= x=1, …, |li| Relevance(tx , tj) + ( 1 - ) y=1, …, |tj| Relevance(li , ly) Relevance(tx , tj) =2 depth(LCS)/(depth(tx)+depth(tj)) Relevance(li , ly) =2 depth(LCS)/(depth(li)+depth(ly))