Chapter 6 The Standard Deviation as a Ruler






















- Slides: 28

Chapter 6 The Standard Deviation as a Ruler and the Normal Model Copyright © 2009 Pearson Education, Inc.

Objectives: n The student will be able to: n Compare values from two different distributions using their z-scores. n Use Normal models (when appropriate) and the 68 -95 -99. 7 Rule to estimate the percentage of observations falling within one, two, or three standard deviations of the mean. n Determine the percentages of observations that satisfy certain conditions by using the Normal model and determine “extraordinary” values. Copyright © 2009 Pearson Education, Inc. Slide 1 - 2

Standardizing with z-scores n n We compare individual data values to their mean, relative to their standard deviation using the following formula: We call the resulting values standardized values, denoted as z. They can also be called z-scores. Copyright © 2009 Pearson Education, Inc. Slide 1 - 4

Benefits of Standardizing n n n Standardized values have been converted from their original units to the standard statistical unit of standard deviations from the mean. Thus, we can compare values that are measured on different scales, with different units, or from different populations. Example – Which student performed better? Student A received a 85 on a 100 point quiz with a mean of 90 and standard deviation of 5. Student B received a 35 on a 50 point quiz with a mean of 37 and a standard deviation of 3. We must compare z-scores! Copyright © 2009 Pearson Education, Inc. Slide 1 - 6

Examples n n Suppose your stats professor reports your test grade as a z-score and you received a score of 2. 20. What does that mean? Text #14, 15, 20 Copyright © 2009 Pearson Education, Inc. Slide 1 - 7

Back to z-scores n Standardizing data into z-scores shifts the data by subtracting the mean and rescales the values by dividing by their standard deviation. n Standardizing into z-scores does not change the shape of the distribution. n Standardizing into z-scores changes the center by making the mean 0. n Standardizing into z-scores changes the spread by making the standard deviation 1. Copyright © 2009 Pearson Education, Inc. Slide 1 - 8

When Is a z-score BIG? n n n A z-score gives us an indication of how unusual a value is because it tells us how far it is from the mean. Remember that a negative z-score tells us that the data value is below the mean, while a positive z-score tells us that the data value is above the mean. The larger a z-score is (negative or positive), the more unusual it is. Copyright © 2009 Pearson Education, Inc. Slide 1 - 9

When Is a z-score Big? (cont. ) n n There is no universal standard for z-scores, but there is a model that shows up over and over in Statistics. This model is called the Normal model (You may have heard of “bell-shaped curves. ”). Normal models are appropriate for distributions whose shapes are unimodal and roughly symmetric. These distributions provide a measure of how extreme a z-score is. Copyright © 2009 Pearson Education, Inc. Slide 1 - 10

When Is a z-score Big? (cont. ) n n Once we have standardized, we need only one model: n The N(0, 1) model is called the standard Normal model (or the standard Normal distribution). Be careful—don’t use a Normal model for just any data set, since standardizing does not change the shape of the distribution. Copyright © 2009 Pearson Education, Inc. Slide 1 - 13

Checking Conditions… n n When we use the Normal model, we are assuming the distribution is Normal. We cannot check this assumption in practice, so we check the following condition: n Nearly Normal Condition: The shape of the data’s distribution is unimodal and symmetric. n This condition can be checked by making a histogram or a Normal probability plot (to be explained later). n Depending on the type of data, a Normal Model can be assumed Slide 1 - 14 Copyright © 2009 Pearson Education, Inc.

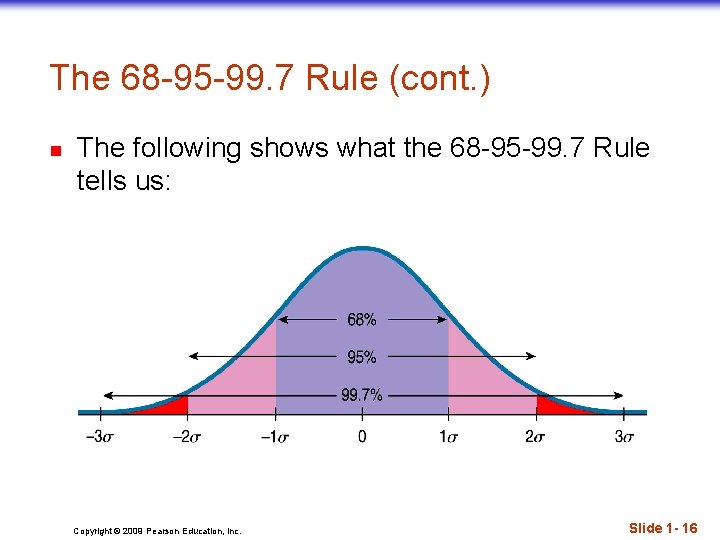
The 68 -95 -99. 7 Rule (cont. ) n n Normal models give us an idea of how extreme a value is by telling us how likely it is to find one that far from the mean. It turns out that in a Normal model: n about 68% of the values fall within one standard deviation of the mean; n about 95% of the values fall within two standard deviations of the mean; and, n about 99. 7% (almost all!) of the values fall within three standard deviations of the mean. Copyright © 2009 Pearson Education, Inc. Slide 1 - 15

The 68 -95 -99. 7 Rule (cont. ) n The following shows what the 68 -95 -99. 7 Rule tells us: Copyright © 2009 Pearson Education, Inc. Slide 1 - 16

Finding Normal Percentiles by Hand n n When a data value doesn’t fall exactly 1, 2, or 3 standard deviations from the mean, we can look it up in a table of Normal percentiles. Table Z in Appendix D provides us with normal percentiles, but many calculators and statistics computer packages provide these as well. Copyright © 2009 Pearson Education, Inc. Slide 1 - 17

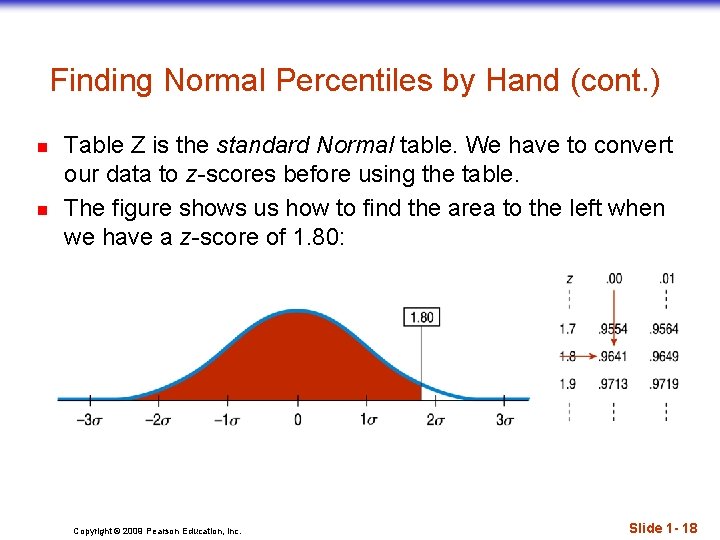
Finding Normal Percentiles by Hand (cont. ) n n Table Z is the standard Normal table. We have to convert our data to z-scores before using the table. The figure shows us how to find the area to the left when we have a z-score of 1. 80: Copyright © 2009 Pearson Education, Inc. Slide 1 - 18

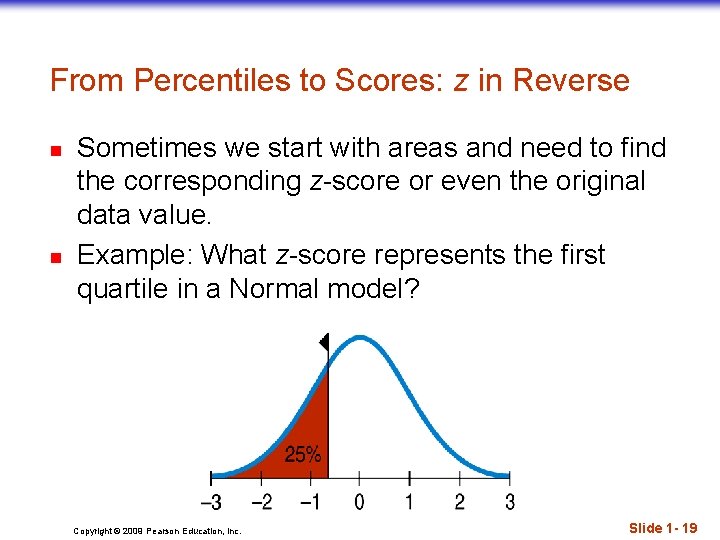
From Percentiles to Scores: z in Reverse n n Sometimes we start with areas and need to find the corresponding z-score or even the original data value. Example: What z-score represents the first quartile in a Normal model? Copyright © 2009 Pearson Education, Inc. Slide 1 - 19

From Percentiles to Scores: z in Reverse (cont. ) n n n Look in Table Z for an area of 0. 2500. The exact area is not there, but 0. 2514 is pretty close. This figure is associated with z = -0. 67, so the first quartile is 0. 67 standard deviations below the mean. Copyright © 2009 Pearson Education, Inc. Slide 1 - 20

Percentiles and Z-scores by hand examples n n What percent of a standard Normal model is found in each region? Draw a picture for each - use Table Z in Appendix D of your text a) z > -2. 05 b) z < -0. 33 c) 1. 2 < z < 1. 8 d) |z| < 1. 28 In a standard Normal model, what value(s) of z cut(s) off the region described? Draw a picture first! a) The highest 20% b) The highest 75% c) The lowest 3% d) The middle 90% Copyright © 2009 Pearson Education, Inc. Slide 1 - 21

Finding Normal Percentiles using Technology – TI-83 n n n To find what percentage of a standard Normal model is found in the region a < z < b (note, for infinity use any large number or 1 E 99!) use the DISTR function normalcdf(a, b) Draw a picture by first setting window to Xmin=-4, Xmax=4, Ymin=-. 1, Ymax=. 4 n Then use DISTR -> DRAW -> Shade. Norm(a, b) Note: we can skip the step of calculating z-scores by giving normalcdf additional parameters: normalcdf(a, b, μ, σ) Copyright © 2009 Pearson Education, Inc. Slide 1 - 22

Finding the z-score given percentile using technology– TI-83 n To find the z-score with a given tail probability, use the DISTR function inv. Norm(p). n we can skip converting from a z-score to a raw score by typing: inv. Norm(p, μ, σ) Copyright © 2009 Pearson Education, Inc. Slide 1 - 23

Percentiles and Z-scores using the TI-83 examples n n What percent of a standard Normal model is found in each region? Draw a picture for each a) z > -1. 05 b) z < -0. 40 c) -. 5 < z < 1. 8 In a standard Normal model, what value(s) of z cut(s) off the region described? Draw a picture first! a) The highest 20% b) The highest 60% c) The lowest 6% d) The middle 75% Copyright © 2009 Pearson Education, Inc. Slide 1 - 24

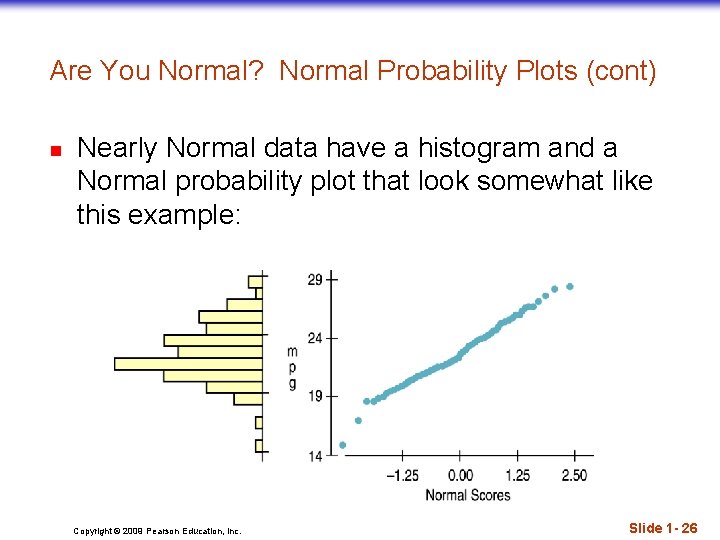
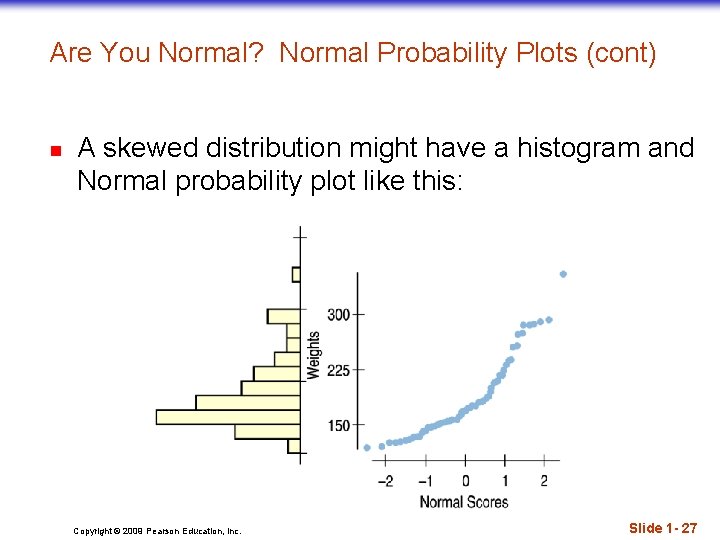
Are You Normal? n n When you actually have your own data, you must check to see whether a Normal model is reasonable. Looking at a histogram of the data is a good way to check that the underlying distribution is roughly unimodal and symmetric. A more specialized graphical display that can help you decide whether a Normal model is appropriate is the Normal probability plot. If the distribution of the data is roughly Normal, the Normal probability plot approximates a diagonal straight line. Deviations from a straight line indicate that the distribution is not Normal. Slide 1 - 25 Copyright © 2009 Pearson Education, Inc.

Are You Normal? Normal Probability Plots (cont) n Nearly Normal data have a histogram and a Normal probability plot that look somewhat like this example: Copyright © 2009 Pearson Education, Inc. Slide 1 - 26

Are You Normal? Normal Probability Plots (cont) n A skewed distribution might have a histogram and Normal probability plot like this: Copyright © 2009 Pearson Education, Inc. Slide 1 - 27

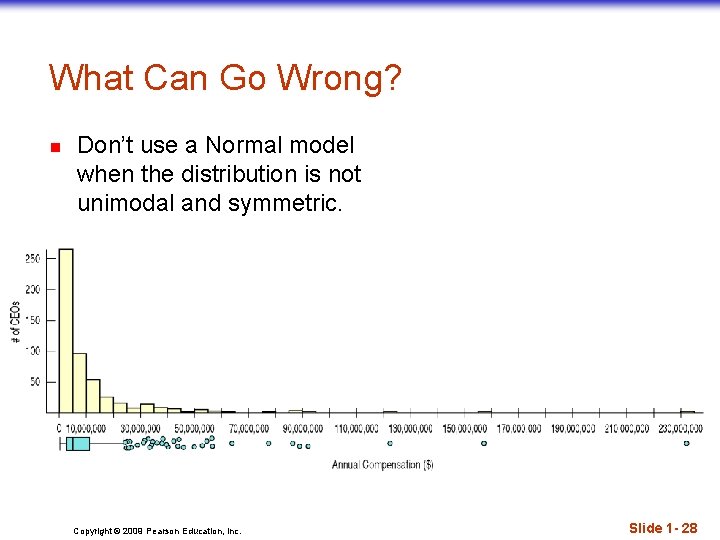
What Can Go Wrong? n Don’t use a Normal model when the distribution is not unimodal and symmetric. Copyright © 2009 Pearson Education, Inc. Slide 1 - 28

What have we learned? (cont. ) n We see the importance of Thinking about whether a method will work: n Normality Assumption: We sometimes work with Normal tables (Table Z). These tables are based on the Normal model. n Data can’t be exactly Normal, so we check the Nearly Normal Condition by making a histogram (is it unimodal, symmetric and free of outliers? ) or a normal probability plot (is it straight enough? ). Copyright © 2009 Pearson Education, Inc. Slide 1 - 29

Additional exercises n Text #28, n Some IQ tests are standardized to a normal model with a mean of 100 and a standard deviation of 16. n n n A) Draw the model for these IQ scores clearly labeling showing what the 68 -95 -99. 7 Rule predicts about the scores B) In what interval would you expect to find the central 95% of IQ scores to be found? C) About what percent of people should have IQ scores above 116? D) About what percent of people should have IQ scores between 68 and 84? E) About what percent of people whould have IQ scores above 132? Copyright © 2009 Pearson Education, Inc. Slide 1 - 30

n n 44) Based on the Normal model N(100, 16) describing IQ scores, what percent of people’s IQ scores would you expect to be n Over 80? n Under 90? n Between 112 and 132? 46) In the same model, what cutoff value bounds n The highest 5% of all IQs? n The lowest 30% of the IQs? n The middle 80% of the IQs? Copyright © 2009 Pearson Education, Inc. Slide 1 - 31

n #32) A company that manufactures rivets believes the shear strength in pounds is modeled by N(800, 50). n n Draw and label the Normal Model Would it be safe to use these rivets in a situation requiring a shear strength of 750 pounds? Explain? About what percent of rivets would you expect to fall below 900 pounds? Rivets are used in a variety of applications with varying shear strength requirements. What is the maximum shear strength for which you would feel comfortable approving this company’s rivets? Explain. Copyright © 2009 Pearson Education, Inc. Slide 1 - 32
 Standard deviation as a ruler and the normal model
Standard deviation as a ruler and the normal model Chapter 6 the standard deviation as a ruler
Chapter 6 the standard deviation as a ruler How do i find the mean absolute deviation?
How do i find the mean absolute deviation? Standard error formula
Standard error formula How to find percentile rank
How to find percentile rank Standard deviation for grouped data
Standard deviation for grouped data Standard deviation symbols
Standard deviation symbols Variance standard deviation formula
Variance standard deviation formula Ran# calculator
Ran# calculator Standard deviation ap biology
Standard deviation ap biology Matthew coignet
Matthew coignet Uncertainty propagation
Uncertainty propagation Xi in standard deviation formula
Xi in standard deviation formula Effect size formula
Effect size formula Standard deviation 66 95 99
Standard deviation 66 95 99 99% z*
99% z* Standard deviatio symbol
Standard deviatio symbol Standard deviation sxx
Standard deviation sxx Alternate formula for standard deviation
Alternate formula for standard deviation Standard deviation in continuous series
Standard deviation in continuous series Standard deviation in chemistry
Standard deviation in chemistry Standard deviation
Standard deviation Standard deviation of sampling distribution of p hat
Standard deviation of sampling distribution of p hat Standard deviation of sampling distribution of p hat
Standard deviation of sampling distribution of p hat How to calculate expected return
How to calculate expected return Portfolio standard deviation
Portfolio standard deviation Standard deviation formula java
Standard deviation formula java How to make residual plot on ti 84
How to make residual plot on ti 84 Rumus linear
Rumus linear