Chapter 5 Nutan S Mishra Department of Mathematics

Chapter 5 Nutan S. Mishra Department of Mathematics and Statistics University of South Alabama

Discrete Variables A random variable is a variable whose value is determined by the outcome of a random experiment. A random variable assigns a numerical value to an event in S Example: In tossing a coin S = {H, T} Define random variable as follows: X = 1 when H occurs X = 0 when T occurs. Here X is a discrete random variable.

Discrete Random Variable In some cases the outcomes of the experiment are themselves numerical values, in such a case we may not have to define a random variable separately. Example: rolling a die S ={1, 2, 3, 4, 5, 6}. All outcomes are numerical thus we do not have to define the random variable separately. Define X = # dots showed up X takes values 1, 2, 3, 4, 5, 6

Discrete Random variables Toss three coins and note the number of heads showed up. Let X = # heads occurred. Then x can take the values 0, 1, 2, 3 Number of vehicles owned by a family Number of dependents in a family Number of goals scored by a player

Continuous Random Variable • When outcomes of an experiment are numerical values in an interval then X is continuous • Example: Recording the GPA of students • X = GPA of a student • Then X [0, 4] and X can take any value in this interval. • X= highest temperature on a given day • X= Time taken by a runner to complete a race.

Probability Distribution Probability distribution of a discrete random variable is the set of all values of X and the set of corresponding probabilities P(X=x). Example: toss a single coin and observe the number of heads occurred. Define X = # heads Then X can take two values 0 or 1 X P(X=x) 0 . 5 1 . 5 These two columns together are called probability distribution of X

Probability distribution Toss three coins and define X = # heads then X=0, 1, 2, 3 S = {TTT, TTH, THT, HTT, HHT, HTH, THH, HHH} The probability distribution x is : X P(X=x ) 0 1/8 1 3/8 2 3/8 3 1/8

Properties of distribution P(X=x) is denoted by f(X=x) or just f(x) is called probability mass function. Two properties 1. f(x) 0 2. f(x) = 1 X P(X=x )=f(x) X P(X=x) = f(x) 0 . 5 0 1/8 1 . 5 1 3/8 2 3/8 3 1/8

Exercise 5. 8 x P(x) 0 . 10 2 . 35 1 . 05 3 . 28 2 . 45 4 . 20 3 . 40 5 . 14 ΣP(x) = 1. 00 x P(x) 7 -. 25 8 . 85 9 . 40 ΣP(x) = 1. 00 ΣP(x) =. 97

Exercise 5. 10 x 0 1 2 3 4 5 6 P(x) . 11 . 19 . 28 . 15 . 12 . 09 . 06 a. P(x=3) =. 15 b. P(x ≤ 2) = P(x=0)+P(x=1)+P(x=2) = c. P(x ≥ 4) = P(x=4)+P(x=5)+P(x=6) = d. P(1 ≤x ≤ 4) = P(x=1)+P(x=2)+P(x=3)+P(x=4) e. P(x<4) = 1 - P(x ≥ 4) f. P(x>2) = 1 - P(x ≤ 2) g. P(2 ≤x ≤ 5) = P(x=2)+P(x=3)+P(x=4)+p(x=50)

Exercise 5. 14 X = # TV sets owned by a family Size of the dataset is 2500 (This is a population) Use classical approach to find probability distribution of x. # TV sets owned (x) # families (f) P(x) 0 120 . 048 1 970 . 388 a. The two highlighted columns together form the probability distribution of X b. These probabilities are exact because this is a 3 410. 164 population data and we 4 270. 108 are using classical approach to compute sum 2500 1. 00 probabilties. C. P(x=1) =. 388, P(x≥ 3) = P(x=3)+P(x=4) =. 064+. 108 2 730 . 292 P(2 ≤ x ≤ 4) = P(x=2)+P(x=3)+P(x=4) =. 292+. 064+. 108 P(x<4) = 1 -P(x≥ 4) = 1 -P(x=4) = 1 -. 108

Mean of a discrete random variable x is the value that is expected to occur per repetition of the experiment. # TV sets owned (x) P(x) x. P(x) 0 . 048 0 1 . 388 2 . 292 . 584 3 . 164 . 492 4 . 108 . 432 sum 1. 00 Σx. P(x)=1. 896 Mean = 1. 896 TV sets Interpretation : If we repeat this experiment number of times then on the average a family owns 1. 896 TV sets.

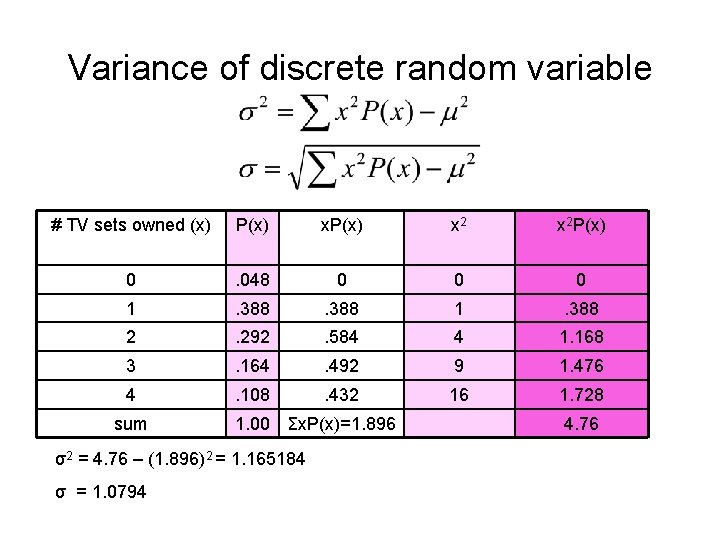
Variance of discrete random variable # TV sets owned (x) P(x) x 2 P(x) 0 . 048 0 0 0 1 . 388 2 . 292 . 584 4 1. 168 3 . 164 . 492 9 1. 476 4 . 108 . 432 16 1. 728 sum 1. 00 Σx. P(x)=1. 896 σ2 = 4. 76 – (1. 896)2 = 1. 165184 σ = 1. 0794 4. 76

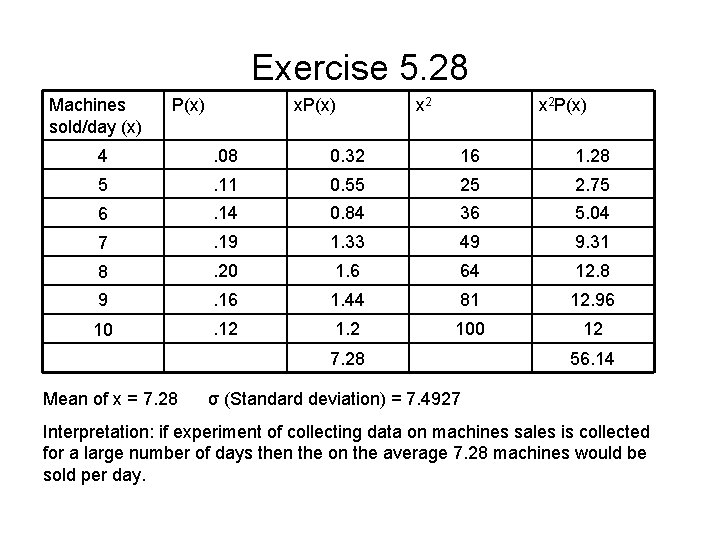
Exercise 5. 28 Machines sold/day (x) P(x) x 2 P(x) 4 . 08 0. 32 16 1. 28 5 . 11 0. 55 25 2. 75 6 . 14 0. 84 36 5. 04 7 . 19 1. 33 49 9. 31 8 . 20 1. 6 64 12. 8 9 . 16 1. 44 81 12. 96 10 . 12 1. 2 100 12 7. 28 Mean of x = 7. 28 56. 14 σ (Standard deviation) = 7. 4927 Interpretation: if experiment of collecting data on machines sales is collected for a large number of days then the on the average 7. 28 machines would be sold per day.

Counting revisited Useful links: http: //www. unc. edu/~knhighto/econ 70/lec 4. htm http: //pavlov. psyc. queensu. ca/~flanagan/20 2_1999/lecture 9. html

Factorials Example: three students with names A B C and three chairs red blue and yellow. Question: in how many ways students can be allocated to the chairs? A B C A C B B A C B C A B C B In general n distinct objects can be arranged in n places in n! (factorial n) ways n! = n*(n-1)*…*1 3! = 3*2*1 = 6 ways A

Permutations Example: four students A B C D and two chairs Question: How many ways a team of two students can occupy the chairs? A B A C A D B C B D C D B A C A D A C B D C # ways we can arrange n items in r places Is called permutation n. Pr = n*(n-1)*…(n-r+1) 4 P 2 = 4*3 = 12

Combinations Example: four students A B C D and two identical chairs. Question: In how many ways we can allocate students to the chairs? A B A C A D B C B D C D Here order does not matter (that is it does not matter which student occupies which chair because chairs are identical) # ways choosing r items out of n distinct items is 4 C 2 = 6 Table III on page C 7 lists the values of combinations

Bernoulli trials An experiment which has only two possible outcomes is a Bernoulli trial with probability of one outcome p and that of the other as 1 -p. Example: toss a coin : has only two outcomes H and T if P(H) =. 5 then P(T) = 1 -. 5 =. 5 If the coin is not fair and P(H) =. 7 then P(T) = 1 -. 7 =. 3

Bernoulli distribution More examples of Bernoulli trials: Inspecting a car at an assembly plant and declaring it as lemon or good. If P(L) =. 001 then P(G) =. 999 People entering into a football stadium. Classifying them into one of the genders. M or F if P(M) =. 62 then P(F) =. 38

Binomial Experiment A binomial experiment consists of n independent Bernoulli trials. That is repeating the Bernoulli experiment n times. Each repetition is independent of the other. Example: Toss three fair coins. n=3 Each coin is a Bernoulli trial. Outcome of one toss does not affect that of the others i. e. all tosses are independent. And p=. 5 for all the three tosses.

Binomial experiment Definition: 1. The experiment consists of n identical trials. 2. Each trial has only two possible outcomes 3. The probability of outcomes remain constant at each trial. 4. The trials are independent.

Binomial probability distribution In a Binomial experiment define a random variable x as X =# heads occurred in n tosses or X = # successes in n trials. Then x takes values 0, 1, 2 …, n Such an X is called Binomial random variable with n and p specified. If we repeat the binomial experiment a large number of times then we are interested probabilities of x assuming different values i. e in tossing n coins what is P(X=0) or P(X=1) and so on In other words we are interested in probability distribution of x.

Binomial distribution Consider a binomial experiment with n trials and p as probability of success in a single trial then X = # successes in n independent trials is a binomial variable and its probability distribution is called Binomial distribution with parameters n and p P(x=k) = n. Ck pk (1 -p)n-k for x = 0, 1, …n Alternatively replace 1 -p =q P(x=k) = n. Ck pk qn-k for x = 0, 1, …n

Exercise 5. 51 a. b. c. Rolling a die many times and observing # spots is not a binomial experiment because there are more than two possible outcomes of a roll Rolling a die many times and observing whether the number is even or odd is a binomial experiment because at each roll there are only two possible outcomes: even or odd. Besides all the rolls are independent. Yes this a binomial experiment because we are selecting a few people, each person has only two possible answers: in favor or not in favor. The probability of an individual being in favor is known i. e. . 54 and all persons answers are independent.

Exercise 5. 53 a. x= binomial vairate with n=8 and p=. 7 P(x=5) = 8 C 5 *p 5 (1 -p)8 -5 = 8 C 5 *p 5 (1 -p)3 = 8 C 5 *(. 7)5 (. 3)3 =. 2441 (from table iv) b. Given n=4, p=. 40 P(x=3) = 4 C 3 *p 3 (1 -p)4 -5 = 4 C 3 *(. 4)3 (. 6) =

Mean and Variance of binomial Let x be a binomial variable with parameters n and p. then mean of x µ = Σx. n. Ck pk (1 -p)n-k = np µ = np Variance σ2 = npq

Exercise 5. 58 Question asked: Do you eat home cooked food three or more times a week? Yes: 85% No: 15% P(Y) = p =. 85 P(N) = 1 -p =q =. 15 a. n=12 (a random sample of 12 Americans) is selected X = # Americans from the sample of 12 who say Yes Then X has binomial distribution with parameters n=12 and p=. 85 X may take values between 0 to 12 That is there may be o Americans who say yes or may be 2. . 0 r at the most 12 will say yes. b. What is the probability that 10 out of 12 Americans say yes to the posed question? P(X=10) = 12 C 10 *p 10(1 -p)12 -10 = 12 C 10 *p 10(1 -p)2