Chapter 40 De Moivres Theorem simple applications 1122020













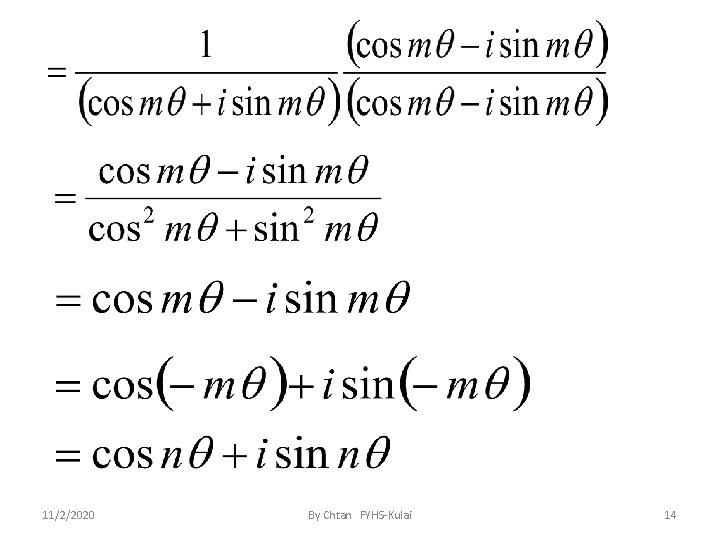















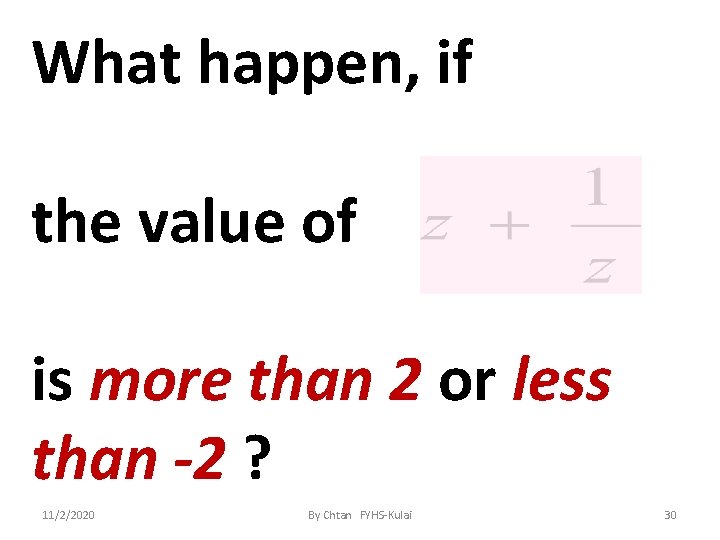










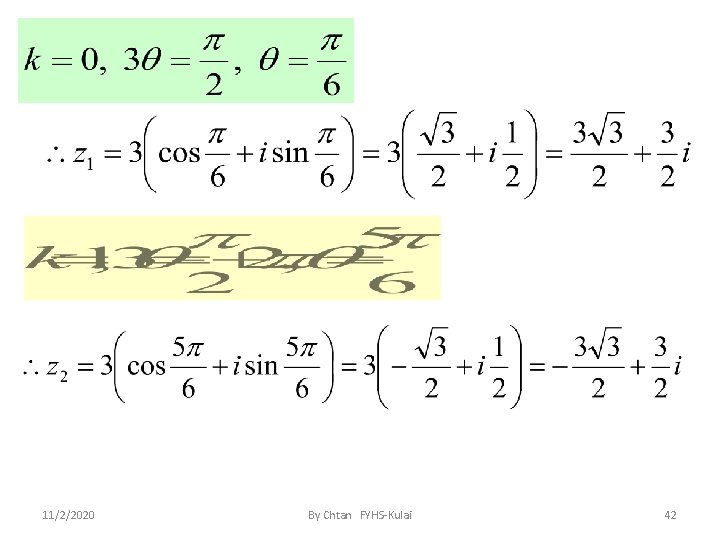










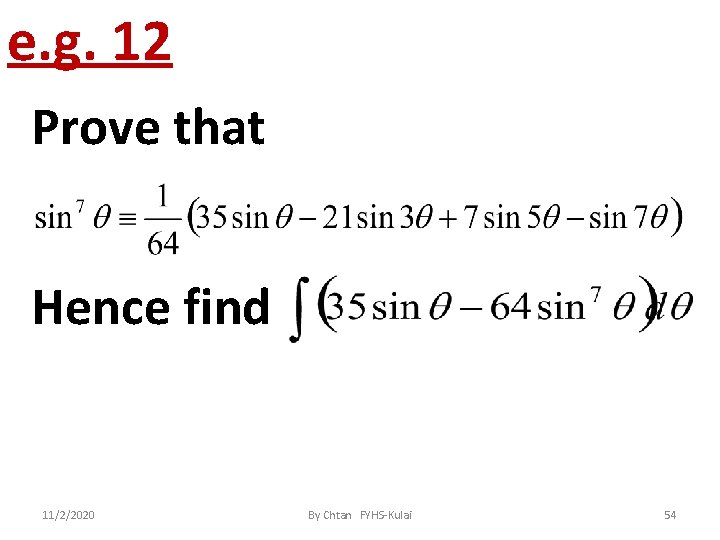









- Slides: 63

Chapter 40 De Moivre’s Theorem & simple applications 11/2/2020 By Chtan FYHS-Kulai 1

In mathematics, de Moivre‘s formula, named after Abraham de Moivre. 11/2/2020 By Chtan FYHS-Kulai 2

The formula is important because it connects complex numbers and trigonometry. The expression "cos x + i sin x" is sometimes abbreviated to "cis x". 11/2/2020 By Chtan FYHS-Kulai 3

By expanding the left hand side and then comparing the real and imaginary parts under the assumption that x is real, it is possible to derive useful expressions for cos(nx) and sin(nx) in terms of cos(x) and sin(x). 11/2/2020 By Chtan FYHS-Kulai 4

Furthermore, one can use a generalization of this formula to find explicit expressions for the n-th roots of unity, that is, complex numbers z such that zn = 1. 11/2/2020 By Chtan FYHS-Kulai 5

De Moivre’s theorem For all values of n, the value, or one of the values in the case where n is fractional, of is 11/2/2020 By Chtan FYHS-Kulai 6

Proofing of De Moivre’s Theorem 11/2/2020 By Chtan FYHS-Kulai 7

Now, let us prove this important theorem in 3 parts. 1. When n is a positive integer 2. When n is a negative integer 3. When n is a fraction 11/2/2020 By Chtan FYHS-Kulai 8

Case 1 : if n is a positive integer 11/2/2020 By Chtan FYHS-Kulai 9

11/2/2020 By Chtan FYHS-Kulai 10

11/2/2020 By Chtan FYHS-Kulai 11

Continuing this process, when n is a positive integer, 11/2/2020 By Chtan FYHS-Kulai 12

Case 2 : if n is a negative integer Let n=-m where m is positive integer 11/2/2020 By Chtan FYHS-Kulai 13
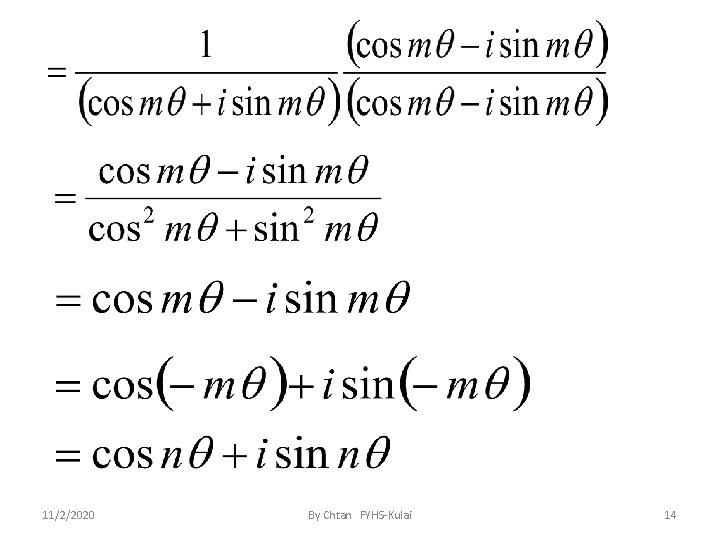
11/2/2020 By Chtan FYHS-Kulai 14

Case 3 : if n is a fraction equal to p/q, p and q are integers 11/2/2020 By Chtan FYHS-Kulai 15

Raising the RHS to power q we have, but, 11/2/2020 By Chtan FYHS-Kulai 16

Hence, De Moivre’s Theorem applies when n is a rational fraction. 11/2/2020 By Chtan FYHS-Kulai 17

Proofing by mathematic al induction 11/2/2020 By Chtan FYHS-Kulai 18

11/2/2020 By Chtan FYHS-Kulai 19

11/2/2020 By Chtan FYHS-Kulai 20

The hypothesis of Mathematical Induction has been satisfied , and we can conclude that 11/2/2020 By Chtan FYHS-Kulai 21

e. g. 1 Let z = 1 − i. Find . Soln: First write z in polar form. 11/2/2020 By Chtan FYHS-Kulai 22

Polar form : Applying de Moivre’s Theorem gives : 11/2/2020 By Chtan FYHS-Kulai 23

It can be verified directly that 11/2/2020 By Chtan FYHS-Kulai 24

Properties of 11/2/2020 By Chtan FYHS-Kulai 25

If then 11/2/2020 By Chtan FYHS-Kulai 26

Hence, 11/2/2020 By Chtan FYHS-Kulai 27

Similarly, if Hence, 11/2/2020 By Chtan FYHS-Kulai 28

We have, Maximum value of cosθ is 1, minimum value is -1. Hence, normally 11/2/2020 By Chtan FYHS-Kulai 29
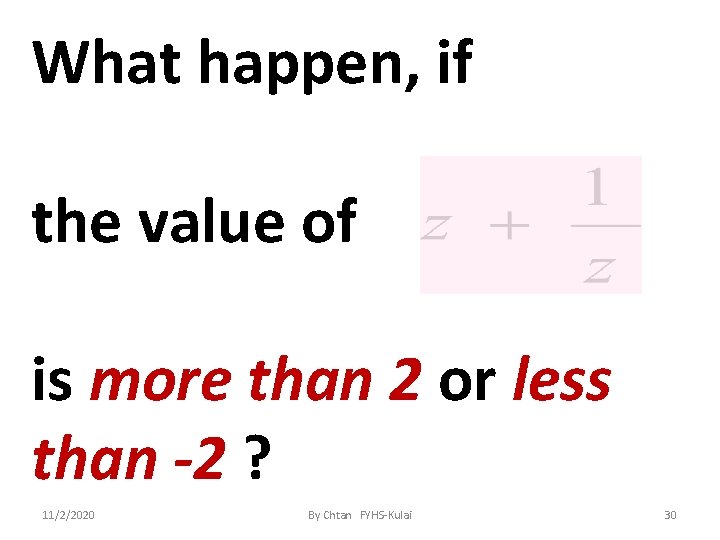
What happen, if the value of is more than 2 or less than -2 ? 11/2/2020 By Chtan FYHS-Kulai 30

e. g. 2 Given that Prove that 11/2/2020 By Chtan FYHS-Kulai 31

e. g. 3 If 11/2/2020 , find By Chtan FYHS-Kulai 32

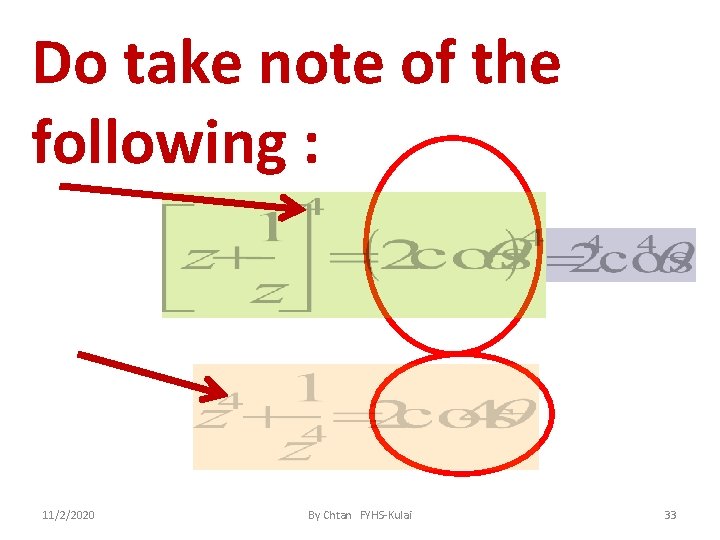
Do take note of the following : 11/2/2020 By Chtan FYHS-Kulai 33

e. g. 4 11/2/2020 By Chtan FYHS-Kulai 34

Applications of De Moivre’s theorem 11/2/2020 By Chtan FYHS-Kulai 35

We will consider three applications of De Moivre’s Theorem in this chapter. 1. Expansion of 2. Values of . 3. Expressions for terms of multiple angles. 11/2/2020 . By Chtan FYHS-Kulai in 36

Certain trig identities can be derived using De Moivre’s theorem. In particular, expression such as can be expressed in terms of : 11/2/2020 By Chtan FYHS-Kulai 37

e. g. 5 Use De Moivre’s Thorem to find an identity for in terms of 11/2/2020 . By Chtan FYHS-Kulai 38

e. g. 6 Soln: Find all complex cube roots of 27 i. We are looking for complex number z with the property Strategy : First we write 27 i in polar form : - 11/2/2020 By Chtan FYHS-Kulai 39

Now suppose Satisfies. Then, by De Moivre’s Theorem, 11/2/2020 By Chtan FYHS-Kulai 40

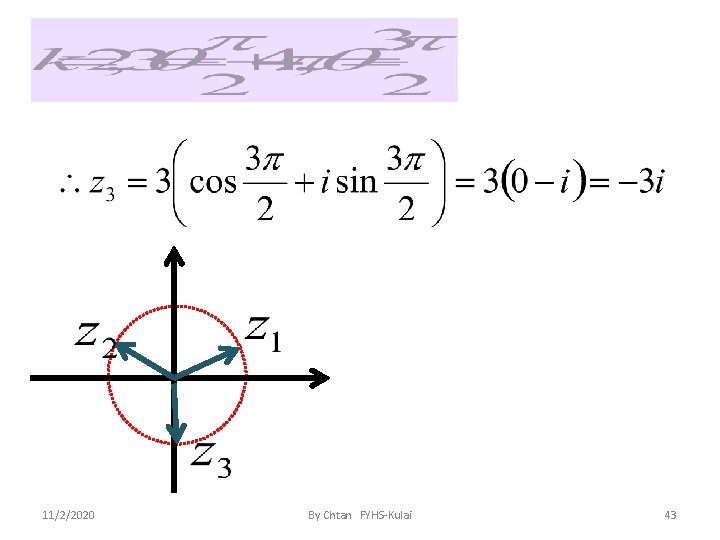
This means : where k is an integer. Possibilities are : k=0, k=1, k=2 11/2/2020 By Chtan FYHS-Kulai 41
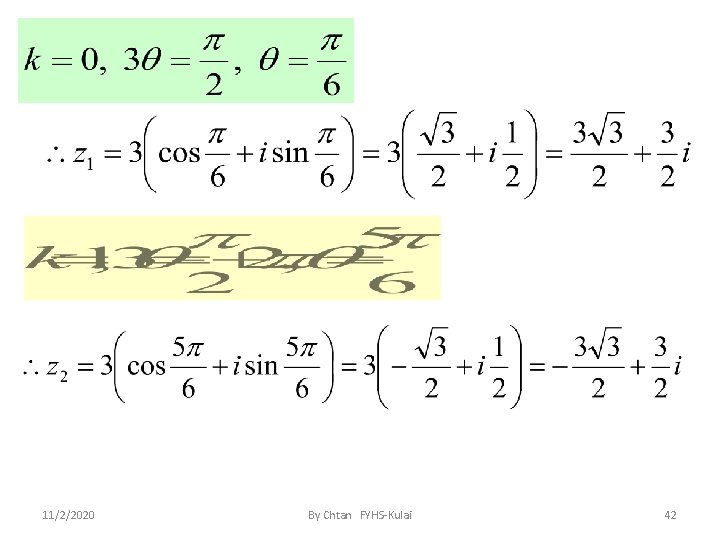
11/2/2020 By Chtan FYHS-Kulai 42

11/2/2020 By Chtan FYHS-Kulai 43

In general : to find the complex nth roots of a non-zero complex number z. 1. Write z in polar form : 11/2/2020 By Chtan FYHS-Kulai 44

2. z will have n different nth roots (i. e. 3 cube roots, 4 fourth roots, etc. ) 3. All these roots will have the same modulus the positive real nth roots of r). 4. They will have different arguments : 11/2/2020 By Chtan FYHS-Kulai 45

5. The complex nth roots of z are given (in polar form) by …etc 11/2/2020 By Chtan FYHS-Kulai 46

e. g. 7 Find all the complex fourth roots of -16. Soln: Modulus = 16 Argument = ∏ 11/2/2020 By Chtan FYHS-Kulai 47

Fourth roots of 16 all have modulus : and possibilities for the arguments are : 11/2/2020 By Chtan FYHS-Kulai 48

Hence, fourth roots of -16 are : 11/2/2020 By Chtan FYHS-Kulai 49

e. g. 8 Given that and find the value of m. 11/2/2020 By Chtan FYHS-Kulai 50

e. g. 9 Solve that 11/2/2020 , hence prove By Chtan FYHS-Kulai 51

e. g. 10 Find the cube roots of -1. show that they can be denoted by and prove that 11/2/2020 By Chtan FYHS-Kulai 52

e. g. 11 Solve the following equations, giving any complex roots in the form 11/2/2020 By Chtan FYHS-Kulai 53
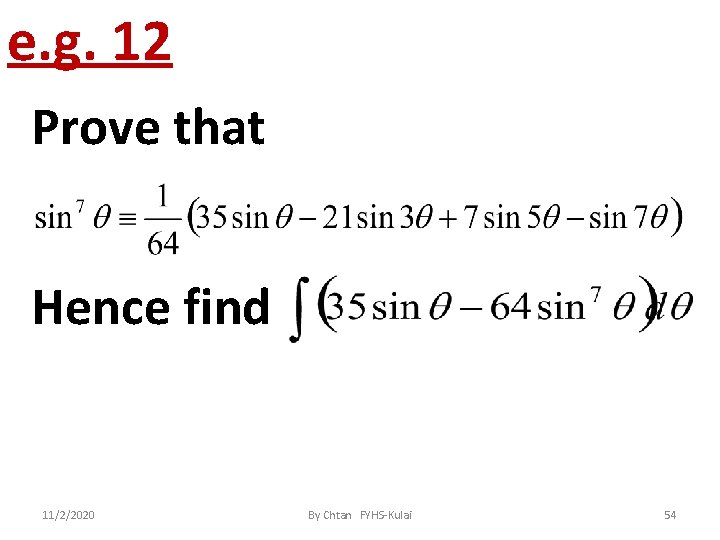
e. g. 12 Prove that Hence find 11/2/2020 By Chtan FYHS-Kulai 54

e. g. 13 Show that Use your result to solve the equation 11/2/2020 By Chtan FYHS-Kulai 55

e. g. 14 Use De Moivre’s Theorem to find 11/2/2020 By Chtan FYHS-Kulai 56

e. g. 15 11/2/2020 By Chtan FYHS-Kulai 57

e. g. 16 11/2/2020 By Chtan FYHS-Kulai 58

e. g. 17 11/2/2020 By Chtan FYHS-Kulai 59

e. g. 18 11/2/2020 By Chtan FYHS-Kulai 60

e. g. 19 Express in terms of multiple angles and hence evaluate 11/2/2020 By Chtan FYHS-Kulai 61

e. g. 20 Express in terms of and hence evaluate terms of. 11/2/2020 By Chtan FYHS-Kulai in 62

The end 11/2/2020 By Chtan FYHS-Kulai 63
 De moivre's theorem and nth roots
De moivre's theorem and nth roots Joanna sokalska
Joanna sokalska 1122020
1122020 Number complex
Number complex De moivre's theorem proof
De moivre's theorem proof Viroots
Viroots Green's theorem stokes theorem divergence theorem
Green's theorem stokes theorem divergence theorem State varignon's theorem.
State varignon's theorem. Pythagoras summary
Pythagoras summary Hahn banach theorem applications
Hahn banach theorem applications Applications of maximum power transfer theorem
Applications of maximum power transfer theorem State remainder theorem
State remainder theorem Factor theorem
Factor theorem Factor theorem and remainder theorem
Factor theorem and remainder theorem Conjugate zeros theorem
Conjugate zeros theorem Rational factor theorem
Rational factor theorem Linear factors theorem and conjugate zeros theorem
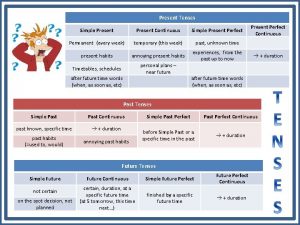
Linear factors theorem and conjugate zeros theorem Present simple and future simple
Present simple and future simple Past simple future simple
Past simple future simple Present simple present continuous past simple future simple
Present simple present continuous past simple future simple Past simple future
Past simple future Simple present simple future
Simple present simple future Future simple in the past
Future simple in the past Have en futuro simple
Have en futuro simple Verbo do presente simples
Verbo do presente simples Future simple present simple
Future simple present simple Chapter 3 skills and applications
Chapter 3 skills and applications Hand signal
Hand signal Chapter 28 unemployment
Chapter 28 unemployment Chapter 23:1 performing range of motion exercises
Chapter 23:1 performing range of motion exercises Chapter 8 linear programming applications solutions
Chapter 8 linear programming applications solutions Chapter 4 applications of derivatives
Chapter 4 applications of derivatives The life skill using community resources means
The life skill using community resources means Line regulation
Line regulation Chapter 4 applications of derivatives
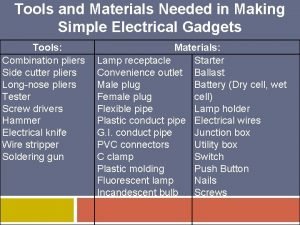
Chapter 4 applications of derivatives Give at least five tools in making simple electrical gadget
Give at least five tools in making simple electrical gadget X simple and y simple
X simple and y simple Simple predicate meaning
Simple predicate meaning Past simple vs past continuous structure
Past simple vs past continuous structure Present simple perfect
Present simple perfect Past simple and past continuous and past perfect
Past simple and past continuous and past perfect Present past simple
Present past simple Present simple passive gradjenje
Present simple passive gradjenje Presente simple y pasado simple
Presente simple y pasado simple Simple interest formula
Simple interest formula Present simple and past simple passive
Present simple and past simple passive Dress simple past
Dress simple past Revision present simple tense
Revision present simple tense Present simple present continuous past simple
Present simple present continuous past simple Awake past form
Awake past form Present simple present continuous or past simple
Present simple present continuous or past simple Andy sometimes read comics
Andy sometimes read comics Present progressive review
Present progressive review If present simple present simple
If present simple present simple Simple past vs simple present
Simple past vs simple present When do we use past simple tense
When do we use past simple tense Simple past simple future
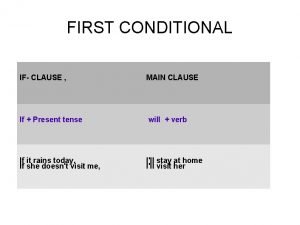
Simple past simple future If + present continuous
If + present continuous Reported statements present simple
Reported statements present simple Simple subject and simple predicate examples
Simple subject and simple predicate examples Present simple tense verb
Present simple tense verb Underline the complete subject
Underline the complete subject Compound predicate
Compound predicate Being with past participle
Being with past participle