Chapter 3 Expressions Expression term op term Eg

Chapter 3 Expressions

Expression term op term Eg. n 1 + n 2 term constant 1, 2. 3 variable n 1, x method call read. Int(. . . ) expression in parentheses (n 1 + 2)

Primitive Data Types A data type is defined by two properties: – Domain – Set of operations Example int. . . -2, -1, 0, 1, 2, . . . +, -, *, / Primitive data types in Java: byte, short, int, long, float, double, char, boolean String can be viewed as a primitive type.

Primitive Data Types in Java • byte (8 bits) range: -128 (-2^(7)) to 127 (2^(7) – 1) • int (32 bits) range: -2147483648 (-2^(31)) to 2^(31) – 1 • float (32 bits) range: +-1. 4 x 10^(-45) (+-2^(-23) x 2^(-126)) to +-3. 4 x 10^(38) (+-(2. 0 – 2^(-23)) x 2^(127) (IEEE floating-point standard, single precision)

Constants • integer constants: -123, 456 • floating-point constants: -1. 23 E 3, 4. 56 E(-1), 7. 8 • boolean constants: true, false • string constants: “Hello, world”

Variables A placeholder for a value. Three attributes: name (ring. Width) value (4) type (int)

Naming convention Use meaningful names for readability. • variable names Begin with a lowercase letter. Each additional word is capitalized. (number. Of. Students) • class names Begin with an uppercase letter. Each additional word is capitalized. (Hello. Program) Do not use the reserved words. (P. 63)

Declarations Syntax: type identifier = expression; Examples int double n 1 = 3; width = 6. 5; A variable must be declared before it is used.

Types of variables • Local variables Declared inside a method. They are local (only available to that method). public class Class. Name … { public void run() { int height = 50; … } } Same variable name can be used in different methods.

Types of variables • Instance variables Declared within the definition of a class, but outside of any method in that class. Stored as part of each object (instance of a class). Avoid it for now. • Class variables Defined at class level, include the keyword static syntax: type static id = exp; Right tool for named constants (next). Shared by all methods in the class and all instances of the class.

Named constants Define constants as (static) variables. Syntax private static final type id = exp; private only available within this class static class (not instance) variable final constant (cannot be changed after initialization)

Why named constants? • Maintainability Change one for all, avoid missing updates • Avoid typing errors • Improve readability PI vs 3. 14 (3. 1416) • Naming convention: Uppercase letters, separate words by “_”

Example: Define constants as (static) variables /* * File: Inches. To. Centimeters. java * --------------------* This program prompts for inches and converts inches to centimeters. */ Import acm. program. *; Public class Inches. To. Centimeters extends Console. Program { public void run() { println(“This program converts inches to centimeters. ”); double inches = read. Double(“Enter value in inches: “); double cm = inches*CENTIMETERS_PER_INCH; println(inches + “in = “ + cm + “cm”); } /* private constant */ private static final double CENTIMETER_PER_INC = 2. 54; }

GRect. Plus. GOval revisited /* * File: GRect. Plus. GOval. java * -----------------* This program draws a red GRect and a green * GOval. It illustrates the use of variables as * constants. /* import acm. graphics. *; acm. program. *; java. awt. *;

public class GRect. Plus. GOval extends Graphics. Programs { public void run() { int x = (get. Width() – FIGURE_WIDTH) / 2; int y = (get. Height() – FIGURE_HEIGHT) / 2; /* draw a red GRect */ GRect rect = new GRect(x, y, FIGURE_WIDTH, FIGURE_HEIGHT); rect. set. Filled(true); rect. set. Color(Color. RED); add(rect); /* draw an outlined green Goval inside Grect */ GOval oval = new GOval(x, y, FIGURE_WIDTH, FIGURE_HEIGHT); oval. set. Filled(true); oval. set. Fill. Color(Color. GREEN); add(oval); } /* private constants */ private static final int FIGURE_WIDTH = 125; private static final int FIGURE_HEIGHT = 75; }

Operators Arithmetic operators (integers and floatingpoint) + addition subtraction (or negation) * multiplication / division % remainder

Precedence Rule: Use common sense • *, /, % precede +, • Left to right at same level Use parentheses Example Prefer 1 + (2/3) over 1 + 2/3

Assignment statements Syntax var = exp The value of var is overwritten by the value of exp. Type match The type of the value of exp must match the type of var. int n = 1. 99; type mismatch!

Type of the value of an expression Suppose n is of type int. n + 1 is of type int n + 1. 5 is of type double If all operands in an expression are of type int, the value of the expression is of type int. If one of the operands is of type double, the value of the expression is of type double.

Mixing types in an expression Example 9/4 produces 2 (int) 9. 0/4 produces 2. 25 (double) Note, 9. 0 is of type double, default floatingpoint; 9. 0 f is of type float. Automatic conversion In 9. 0/4, integer 4 is automatically converted to double before the division.

Type conversion Explicit conversion (type cast) int n = (int) 1. 99; The value of n is 1. It is advised to use explicit type casting when you mix types in an expression. Prefer (double)n + 1. 5 over n + 1. 5

Type conversion (cont. ) Fallacies Java converts an integer into its mathematically equivalent floating-point. long k = 1801439850948199; (2^(54) + 1) long d = k – (long)((double)k); d = 1! Java converts an integer into its best approximation using floating-point.

Updating a variable var = var op exp; can be shortened to var op= exp; Notice spacing. Example x = x + 2; is the same as x += 2; More examples Balance -= surcharge; Salary *= 2;

A special case Incrementing or decrementing by 1. x++; is the same as x += 1; y--; is the same as y -= 1;

Boolean expressions Value: true, false Relational operators >, >=, <, <=, ==, != applied to atomic data (int, double, not string) Example If value of m is 3 and value of n is 4, m > n, false m != n, true

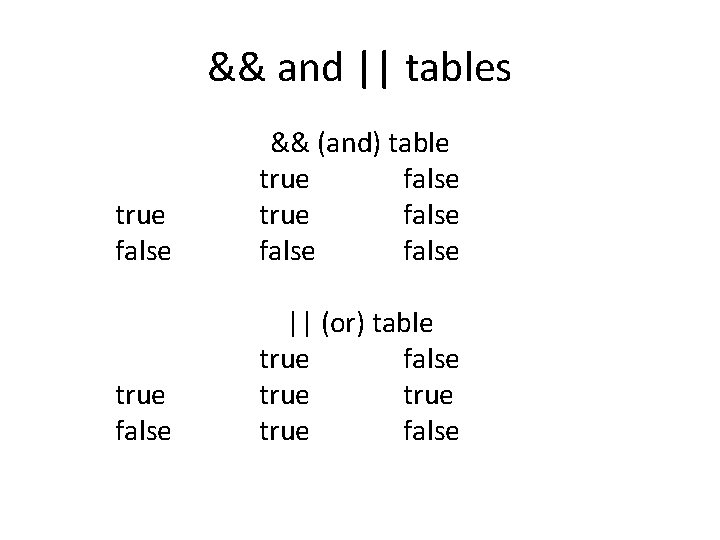
Logic operators !, &&, || (not, and, or) applied to boolean operands. Example If the value of n is 3, n > 2, true n < 4, true (n >2) && (n < 4), true (2<n<4)

&& and || tables true false && (and) table true false true false || (or) table true false true false

More examples If the value of n is 3, n == 3, true n == 2, false (n == 3) && (n == 2), false !((n == 3) && (n == 2)), true !(n == 3) || !(n == 2), true

De Morgan’s Law !(p && q) is equivalent to (!p) || (!q) !(p || q) is equivalent to (!p) && (!q)

Short-circuit evaluation In exp 1 && exp 2 exp 1 is evaluated, if the value is false, then the value of exp 1 && exp 2 is false, regardless of exp 2. Similarly, in exp 1 || exp 2 if the value of exp 1 is true, then the value of exp 1 || exp 2 is true, regardless of exp 2.

Example Is y a multiple of x, for nonzero x? When the value of x is zero, the value of (x != 0) && ((y % x) == 0) is false. Note, the order is important. (x != 0) is the guard. In some languages, when the value of x is zero, (x != 0) && ((y % x) == 0) causes an exception (divided by zero)

Use Boolean variables as flags boolean is. Leap. Year = false; /* a flag is. Leap. Year = (((year % 4) == 0) && (year % 100) != 0)) || ((year % 400) == 0)

Disciplines • Consistent indentations • A space on each side of an operator • Variable names – is. Leap. Year – number. Of. Students • Constant names – FIGURE_WIDTH – MAX_FILE_SIZE • Class names – Inches. To. Centimeters