Chapter 9 Rational Expressions and Equations Basically we

Chapter 9: Rational Expressions and Equations -Basically we are looking at expressions and equations where there is a variable in a denominator

9. 1 Multiplying and Dividing Rational Expressions • • • Definitions and issues Simplifying Multiplying Dividing Complex Fractions

Definition • A rational expression is a ratio of two polynomial expressions • For example, (8 + x) / (13 + x) • Generally, we can simplify rational expressions by cancelling out any factors common to the numerator and denominator • Note that in the expression above, you CANNOT cancel the x terms. . You are NOT allowed to cancel terms that are WITHIN a sum or a difference • To see why, suppose we had (3 + 5) / (3 + 8) • This is equivalent to 8 / 11… BUT if we cancelled the 3’s, we would obtain 5 /8. . Which does NOT equal 8/11!!! • TO SIMPLIFY A RATIONAL EXPRESSION, FACTOR THE NUMERATOR AND THE DENOMINATOR… THEN CANCEL ANY COMMON FACTORS

Issues • Before you simplify a rational expression or combine rational expressions, you must look at the denominator(s) and note any values which, when substituted in for a variable, would cause that denominator to equal zero • These values are called EXCLUDED values • You must find excluded values BEFORE you begin simplifying. . And list them along with your answer • You may need to FACTOR a denominator to determine the excluded values… however, we usually need to factor the denominator ANYHOW • See the examples on the next few slides • Sometimes we ignore excluded values if there are multiple variables in the rational expression

Simplify Look for common factors. 1 Factor. 1 Answer: Simplify.

Under what conditions is this expression undefined? A rational expression is undefined if the denominator equals zero. To find out when this expression is undefined, completely factor the denominator. Answer: The values that would make the denominator equal to 0 are – 7, 3, and – 3. So the expression is undefined at y = – 7, y = 3, and y = – 3. These values are called excluded values.

a. Simplify Answer: b. Under what conditions is this expression undefined? Answer: undefined for x = – 5, x = 4, x = – 4

Multiple-Choice Test Item For what values of p is A 5 B – 3, 5 undefined? C 3, – 5 D 5, 1, – 3 Read the Test Item You want to determine which values of p make the denominator equal to 0.

Solve the Test Item Look at the possible answers. Notice that the p term and the constant term are both negative, so there will be one positive solution and one negative solution. Therefore, you can eliminate choices A and D. Factor the denominator. or Zero Product Property Solve each equation. Answer: B

Multiple-Choice Test Item For what values of p is A – 5, – 3, – 2 Answer: D B – 5 undefined? C 5 D – 5, – 3

Simplify Factor the numerator and the denominator. 1 a or 1 Answer: 1 or –a Simplify.

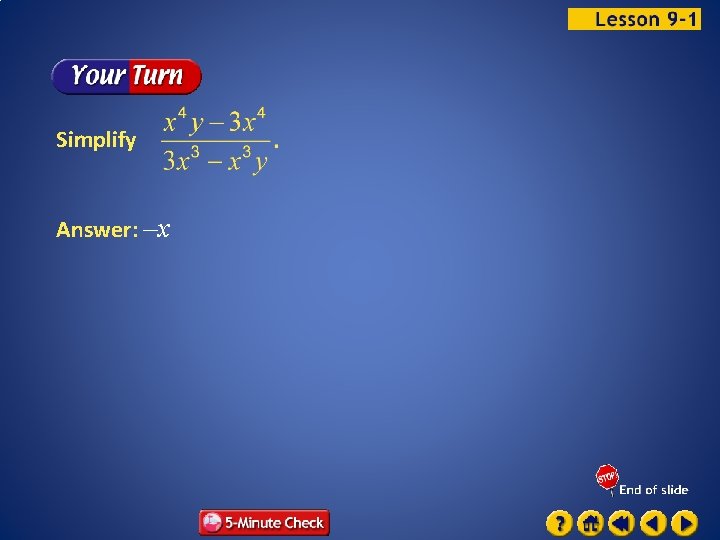
Simplify Answer: –x

Multiplying two rational expressions • Factor the numerator AND denominator of each rational expression • List the excluded values • Cancel any factors common to the numerator and denominator • Multiply the remaining factors in the numerator • Multiply the remaining factors in the denominator • One trick: sometimes it is advantage to factor a negative one (-1) from an expression, if it will allow you to cancel another factor out

Simplify 1 1 1 1 Factor. Simplify. Answer: Simplify. 1

Simplify 1 1 1 1 Factor. Answer: Simplify. 1

Simplify each expression. a. Answer: b. Answer:

Dividing Rational Expressions • Recall that dividing by a fraction is the same as multiplying by the recipricol of that fraction • Generally, it is advisable to rewrite a division problem as a multiplication problem before factoring and cancelling, etc.

Simplify Multiply by the reciprocal of divisor. 1 1 1 Factor. Simplify. Answer: Simplify. 1 1

Simplify Answer:

Simplify Multiply by the reciprocal of the divisor. Answer: 1 – 1 1 1 Simplify.

Simplify Multiply by the reciprocal of the divisor. 1 1 Factor. 1 Answer: 1 Simplify.

Simplify each expression. a. Answer: 1 b. Answer:

COMPLEX FRACTIONS • A complex fraction is a rational expression whose numerator and/or denominator CONTAINS another rational expression! • It’s kind of like a fraction within a fraction • Just remember to treat this problem as a division problem – the numerator is being divided by the denominator

Simplify Express as a division expression. Multiply by the reciprocal of divisor.

1 1 1 – 1 1 1 Factor. Answer: Simplify.

Simplify Answer: