Chapter 21 Cost Minimization Key Concept Cost minimization



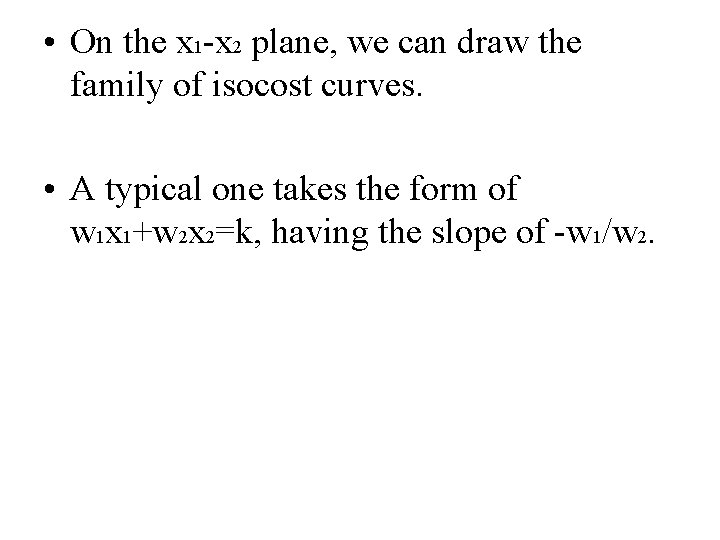



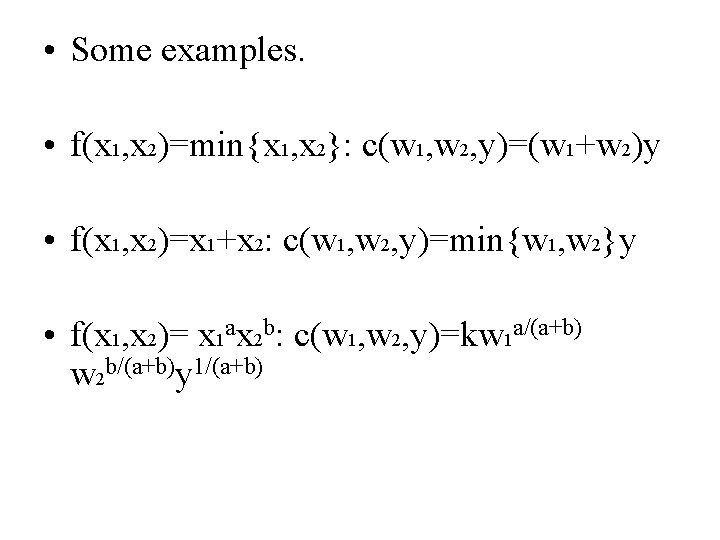




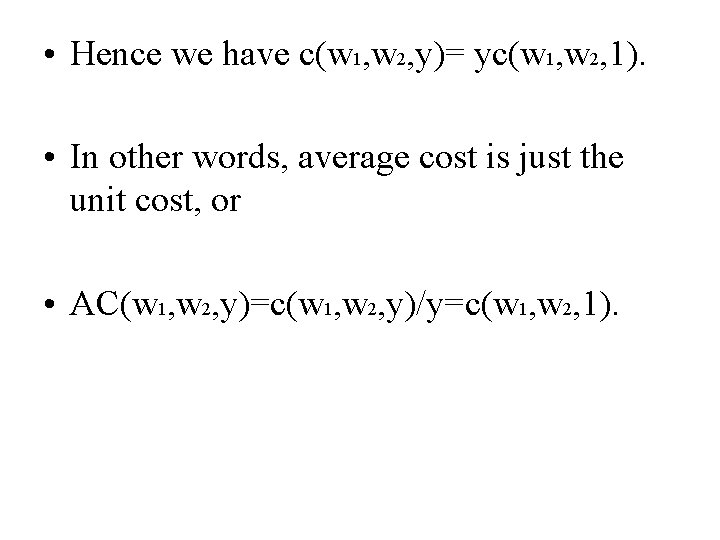










- Slides: 25

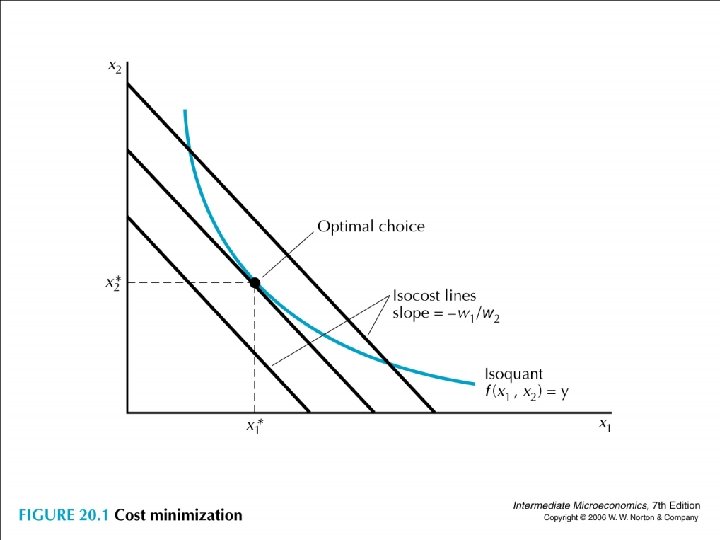
• Chapter 21 Cost Minimization • Key Concept: Cost minimization implies isoquant and isocost are tangent to each other MP 1(x 1*, x 2*)/MP 2(x 1*, x 2*) = w 1/w 2 • LR total cost curve is the lower envelope of the SR total cost curves.

• Chapter 21 Cost Minimization • Break max to • 1) cost min for every y • 2) choose the optimal y* (to max ).

• The cost minimization problems is: minx 1, x 2 w 1 x 1+w 2 x 2 st. f(x 1, x 2)=y • Denote the solution the cost function c(w 1, w 2, y). • It measures the minimal costs of producing y units of outputs when the input prices are (w 1, w 2).
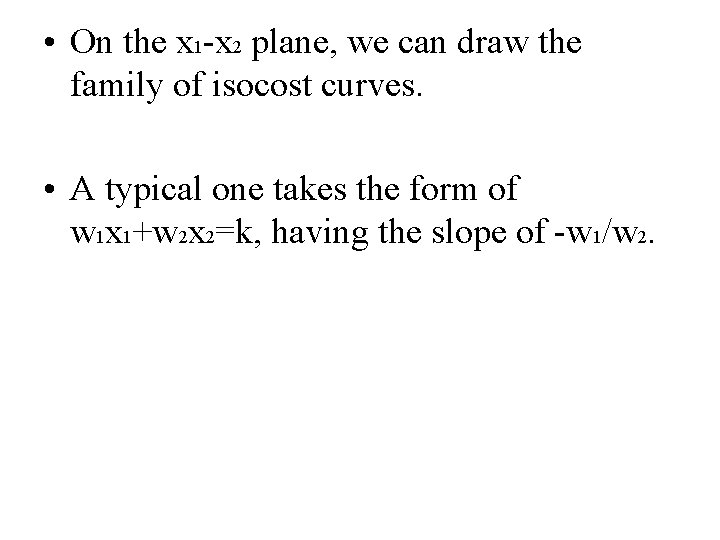
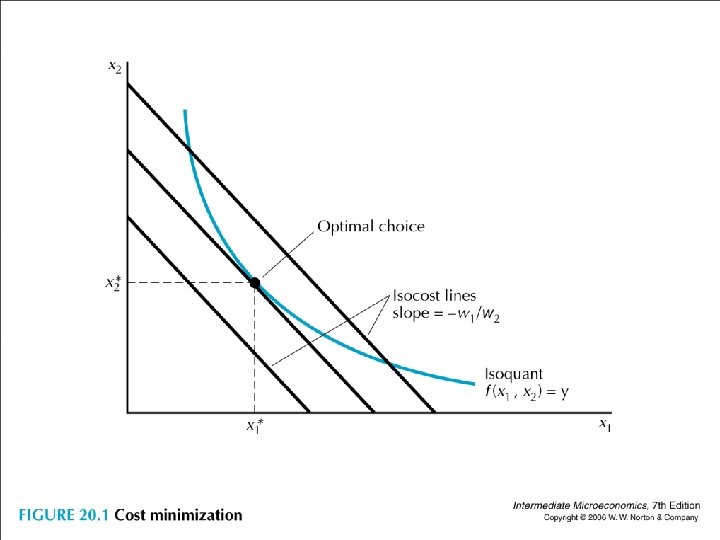
• On the x 1 -x 2 plane, we can draw the family of isocost curves. • A typical one takes the form of w 1 x 1+w 2 x 2=k, having the slope of -w 1/w 2.


• At optimum, the usual tangency condition says that • MRTS 1, 2(x 1*, x 2*) =∆x 2/∆x 1 =-MP 1(x 1*, x 2*)/MP 2(x 1*, x 2*) = -w 1/w 2.

• MRTS 1, 2(x 1*, x 2*) =∆x 2/∆x 1 =-MP 1(x 1*, x 2*)/MP 2(x 1*, x 2*) = -w 1/w 2. • Rearranging to get MP 1(x 1*, x 2*)/w 1= MP 2(x 1*, x 2*)/w 2 an extra dollar spent on recruiting factor 1 or 2 would yield the same extra amount of outputs.


• The optimal choices of inputs are denoted as x 1(w 1, w 2, y) and x 2(w 1, w 2, y). • These are called the conditional factor demands or derived factor demands. • These are hypothetical constructs, usually not observed.
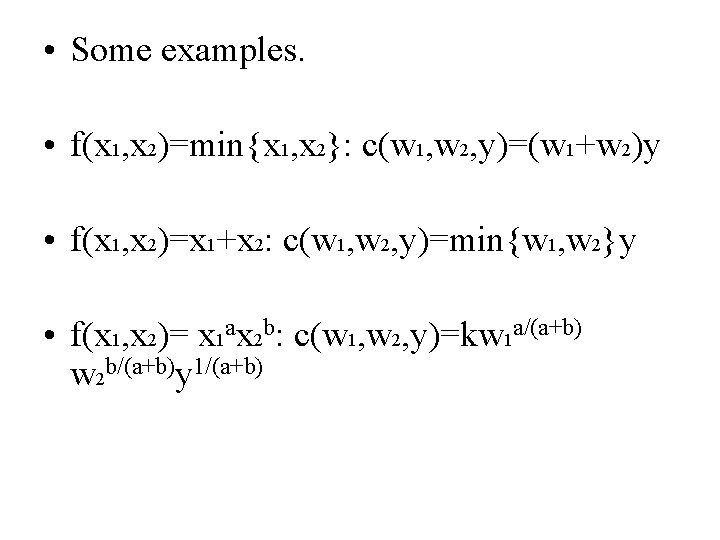
• Some examples. • f(x 1, x 2)=min{x 1, x 2}: c(w 1, w 2, y)=(w 1+w 2)y • f(x 1, x 2)=x 1+x 2: c(w 1, w 2, y)=min{w 1, w 2}y • f(x 1, x 2)= x 1 ax 2 b: c(w 1, w 2, y)=kw 1 a/(a+b) w 2 b/(a+b)y 1/(a+b)

• f(x 1, x 2)= x 1 ax 2 b: c(w 1, w 2, y)=kw 1 a/(a+b) w 2 b/(a+b)y 1/(a+b) • From the Cobb-Douglas example • If CRS a+b=1, then costs are linear in y. • If IRS a+b>1, then costs increase less than linearly with outputs. • If DRS a+b<1, then costs increase more than linearly with outputs. • This holds not only for Cobb-Douglas.

• If CRS, then costs are linear in y. • If IRS, then costs increase less than linearly with outputs. • If DRS, then costs increase more than linearly with outputs.

• Let c(w 1, w 2, 1) be the unit cost. • If we have a CRS tech, what is the cheapest way to produce y units of outputs? • Just use y times as much of every inputs.

• This is true because first, we cannot have c(w 1, w 2, y)> yc(w 1, w 2, 1) since we can just scale everything up. • Now can we have c(w 1, w 2, y)< yc(w 1, w 2, 1)? We cannot either for if so, we can scale everything down.
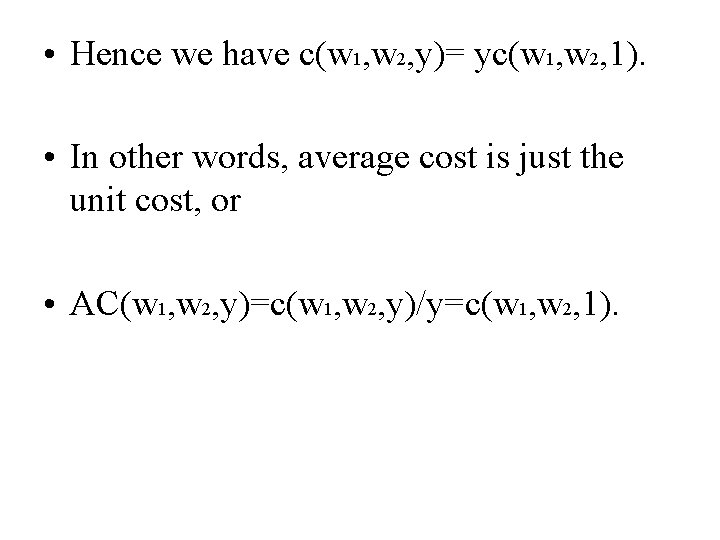
• Hence we have c(w 1, w 2, y)= yc(w 1, w 2, 1). • In other words, average cost is just the unit cost, or • AC(w 1, w 2, y)=c(w 1, w 2, y)/y=c(w 1, w 2, 1).

• What about IRS? • If we double inputs, outputs are more than doubled. • So to produce twice as much outputs as before, we don’t need to double inputs. The costs are thus less than doubled. So AC decreases as y goes up.

• Similarly for DRS, if we halve inputs, outputs are more than a half. • So to produce half as much outputs as before, we can decrease inputs more than a half. • AC decreases as y goes down.

• The assumption of cost minimization has implications on how the conditional factor demands change as the input prices change. • We see the power of revealed cost minimization.

• t: (w 1 t, w 2 t, yt = y) (x 1 t, x 2 t) • s: (w 1 s, w 2 s, ys = y) (x 1 s, x 2 s) • w 1 tx 1 t+w 2 tx 2 t≤ w 1 tx 1 s+w 2 tx 2 s and w 1 sx 1 s+w 2 sx 2 s≤w 1 sx 1 t+w 2 sx 2 t. • Let ∆z=zt-zs. • We have ∆w 1∆x 1+∆w 2∆x 2≤ 0. In other words, the conditional factor demand slopes downwards.



• Intuitively, if in the SR, the fixed factors happen to be at the LR cost minimizing amount, then we don’t have an extra constraint in the SR. • The cost-minimizing amount of the variable inputs in the SR equals that in the LR.

• Normally, cs(x 2, y)≥c(y). • Can we have cs(x 2(y), y)>c(y)? If so, then x 1 s(x 2(y), y)>x 1(y). But notice that in the SR you can also choose x 1(y) to produce y, so this contradicts SR cost minimization. • Hence cs(x 2(y), y)=c(y).

• Sunk costs: expenditures that have been made and cannot be recovered. • They should not affect future decisions. • 100, 000 5 light trucks could sell on the used market for 80, 000, then the sunk cost is 20, 000.

• Chapter 21 Cost Minimization • Key Concept: Cost minimization implies isoquant and isocost are tangent to each other MP 1(x 1*, x 2*)/MP 2(x 1*, x 2*) = w 1/w 2 • LR total cost curve is the lower envelope of the SR total cost curves.
 Cost minimization formula
Cost minimization formula Cost minimization formula
Cost minimization formula Cost minimization
Cost minimization Short run cost minimization
Short run cost minimization Cost minimization analysis
Cost minimization analysis Cost minimization perfect complements
Cost minimization perfect complements Minerals concept map
Minerals concept map Lesson 1 waves answer key
Lesson 1 waves answer key Key partners key activities
Key partners key activities Key partners key activities key resources
Key partners key activities key resources Concept mapping circulation in humans chapter 34
Concept mapping circulation in humans chapter 34 Chapter 28 fishes and amphibians concept mapping answer key
Chapter 28 fishes and amphibians concept mapping answer key Kingdom protista concept map
Kingdom protista concept map Chapter 34 section 1 the circulatory system
Chapter 34 section 1 the circulatory system What is k map definition
What is k map definition Implication table
Implication table Minimization problem example
Minimization problem example Regularized risk minimization
Regularized risk minimization Dual simplex method maximization example
Dual simplex method maximization example Finite state machine minimization
Finite state machine minimization Digital electronics question bank
Digital electronics question bank Dfa minimization code in c++
Dfa minimization code in c++ Big m method minimization example
Big m method minimization example Nfa to dfa subset construction
Nfa to dfa subset construction Basisx
Basisx Interval halving method optimization
Interval halving method optimization