Chapitre CALCUL LITTERAL 09 LT I CONVENTION DECRITURE

Chapitre CALCUL LITTERAL 09 -LT I - CONVENTION D’ECRITURE II – VALEUR NUMERIQUE D’UNE…Exp. III- REDUIRE UNE SOMME IV – SIMPLIFIER UN PRODUIT V - LES PARENTHESES VI - NOTION DE FACTORISATION Bernard 4° Avon

I-CONVENTIONS D’ECRITURE On peut omettre le signe x devant une lettre ou une parenthèse. a x b se note ab 2 x x se note 2 x 3 x(…. . ) se note 3(…. . )x(…. . ) se note 1 x a =a 0 x a = 0 -1 x a = -a -1 x (…. . ) =-(…. ) On lit: 3 facteur de (…. . ) x + x = 2 x x = x² On met les nombres chiffrés devant les lettres On écrit 2 x et non x 2 3(…) et non (…)3

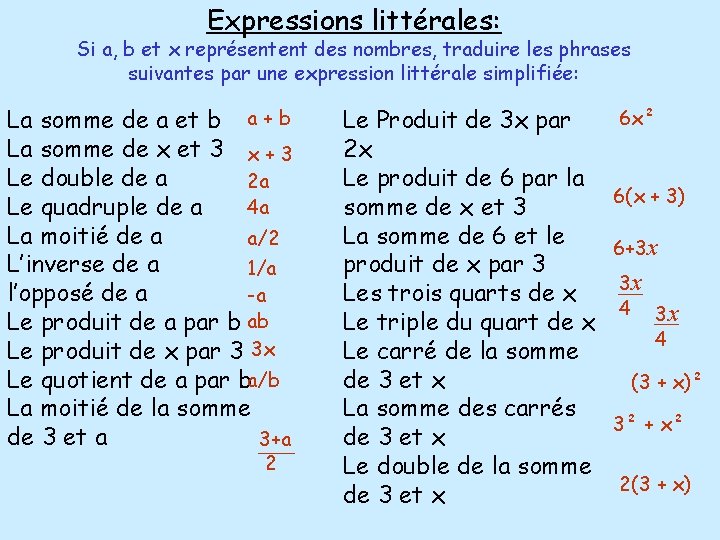
Expressions littérales: Si a, b et x représentent des nombres, traduire les phrases suivantes par une expression littérale simplifiée: La somme de a et b a + b La somme de x et 3 x + 3 Le double de a 2 a 4 a Le quadruple de a La moitié de a a/2 L’inverse de a 1/a l’opposé de a -a Le produit de a par b ab Le produit de x par 3 3 x Le quotient de a par ba/b La moitié de la somme de 3 et a 3+a 2 Le Produit de 3 x par 2 x Le produit de 6 par la somme de x et 3 La somme de 6 et le produit de x par 3 Les trois quarts de x Le triple du quart de x Le carré de la somme de 3 et x La somme des carrés de 3 et x Le double de la somme de 3 et x 6 x² 6(x + 3) 6+3 x 3 x 4 (3 + x)² 3² + x² 2(3 + x)

II-VALEUR NUMERIQUE D’ UNE EXPRESSION A = 5 x + 5 est une expression littéral Si on remplace x par 3, on va trouver la valeur numérique de cette expression pour x = 3 A=5 x 3+5 A =15 + 5 A = 20 Cette expression vaut 20 pour x = 3 Si on remplace x par – 2 A = 5 x(-2) +5 A =-10+5 A = -5 Cette expression vaut -5 pour x = -2

Ex 1: Calculer pour x =1 A=4 x– 4 A =4(1) – 4 A=4– 4 A=0 B = 5 x – 5(x-7) B = 5(1) – 5((1) – 7) B = 5 – 5(-6) B =5 + 30 B =35 C = 2 x² - 3 x + 1 C = 2(1)² - 3(1) + 1 C=2– 3+1 C=0 D = -32 x² + x + 18 D = -32(1)² + 1 +18 D = -32 +19 D = -13

Ex 2: Calculer pour x = -3 A = 4 x – 4 C = 2 x² - 3 x + 1 A = 4(-3) – 4 C = 2(-3)² – 3(-3) +1 A = -12 – 4 C =2 x 9 + 1 A = -16 C = 18 + 10 C = 28 B = 5 x – 5(x-7) D = -32 x² + x + 18 B = 5(-3) – 5((-3)-7) D = -32(-3)² +(-3) + 18 B = -15 – 5(-10) D = -32 x 9 – 3 + 18 B = -15 + 50 D = -288 +15 B = 35 D = - 273

III- REDUIRE UNE SOMME Pour réduire une somme, on regroupe les termes de mêmes « mots mathématiques » , puis on les ajoute ensemble. Ex 1: A = x + 3 x A = 4 x Remarque : on ajoute les x avec les x, les x²avec les x² , les y avec les y et les nombres chiffrés seuls avec les nombres chiffrés seuls. Ex 2: B = x + x² +3 + x + 2 x² + 5 B = x + x² + 2 x² + 3 + 5 B = 2 x + 3 x² + 8

Mais jamais les x avec les x², les a avec les b. . Ex 3: C = x + x² On ne peut pas réduire Ex 4: Réduire l’expression suivante. D = x² + 8 x - 7 - 13 x + 12 + 2 x² + 3 x D = x² + 2 x² + 8 x - 13 x + 3 x - 7 + 12 D = 3 x² - 2 x + 5

Ordonner une expression On range les termes suivant les puissances d’une lettre Ordre croissant Ordre décroissant A = x + 3 x² – 3 A = x + 3 x² - 3 A = -3 + x +3 x² A = 3 x² + x - 3 On a ordonné suivant les puissances de x Ex: Ranger suivant les puissances décroissantes de x: B = 5 x – 5 + 7 x³ - 8 x² B = 7 x³- 8 x² + 5 x - 5

Réduire et ordonner une expression On Réduit en commençant par les puissances 3, puis 2, puis 1, puis 0, ou dans l’autre sens. Ex: A=3 x – 2 x² +5 – 3 – x +7 x² +4 x³ Les x² Les 4 x³ 7 x² 3 x -2 x² -x 5 x² 2 x x Les chiffres 5 -3 2 A = 4 x³ + 5 x² +2 x + 2

IV-REDUIRE ou SIMPLIFIER UN PRODUIT Pour réduire un produit, on multiplie les nombres chiffrés ensemble et les mêmes lettres ensemble Ex 1: A = 3 x x 5 x 2 x A =3 x 5 x 2 x x A = 30 x x² A = 30 x² Ex 2: B = -3 x 5 x x² x 7 x (-x) Signes - par - = + Chiffres 3 x 5 x 7 =105 Lettres x² x x = x³ On utilise la règle du: Signes Chiffres Lettres B = 105 x³

Ex 3 : Réduire les produits suivants. A= 2 xxx 3 xx B = -7 x 3 x C = -5 x x (-4) A= 2 xxx 3 xx B = -7 x 3 x C = (-4) x (-5 x) B = - 21 x C = 20 x A= 2 x 3 xxxx A = 6 x x² A = 6 x² D = -9 x x 6 xy D = -54 x²y

V-LES PARENTHESES 1) Précédées d’un signe + On peut supprimer un couple de parenthèses précédé du signe + A condition qu’il ne soit pas suivi d’un x ou : Ex: A = 8 + (- 3 + x ) A= 8 -3+x A= 5+x

2) Précédées d’un signe On peut supprimer un couple de parenthèses précédé du signe - à condition de changer les signes de tous les termes qui étaient à l’intérieur. A condition qu’il ne soit pas suivi d’un x ou : Ex : A = 8 - ( 4 - 3 x ) A= 8 – (+4 - 3 x) A= 8 - 4 + 3 x A= 4 + 3 x

3) Précédées d’un signe x kx(a+b) =kxa + kxb kx(a-b) =kxa - kxb C’est la formule de la distributivité On dit que l’on a distribué ou développé. Développer une expression littérale, c’est transformer un produit en une somme. Avec les conventions d’écriture on peut écrire: k(a+b) = ka + kb k(a-b) = ka - kb

La double distributivité (a + b) (b + c) = ab + ac + b² + bc (a + b) (b – c) = ab - ac + b² - bc (a – b) (b + c) = ab + ac - b² - bc (a – b) (b – c) = ab - ac - b²+ bc Ex 1: Développer l’expression: (9 +2 x)(7 – 3 x) = 9 x 7 – 9 x 3 x +7 x 2 x - 2 x x 3 x ‘’’’ ‘’’ = 63 - 27 x + 14 x – 6 x² ‘’’’‘’’ = – 6 x² - 13 x + 63

Ex 2 : 143 x 102 = 143 x ( 100 + 2 ) ’’ ’’ ’’ = 143 x 100 = = 14 300 + + 143 x 2 286 14 586 A = 3(- 6 x + 4) B = 2 x (x – y + 4) A = 3 x(- 6 x + 4) B = 2 x x (x – y + 4) A = 3 x(- 6 x) + 3 x 4 B = 2 x x x + 2 x x( - y ) + 2 x x 4 A= -18 x + 12 B = 2 x² - 2 xy + 8 x

Ex 3: 102 x 209 = ( 100 + 2 ) x ( 200 + 9 ) ’’ ’’ ’’ = 100 x 200 + 100 x 9 + 2 x 200 + 2 x 9 = 20 000 + 900 + 400 + 18 = 21 318 A = (2 x + 3)(3 x - 4) A = 2 x x 3 x + 2 x x(- 4) + 3 x 3 x + 3 x(- 4) A= 6 x ² - 8 x + 9 x – 12 A= 6 x² +x – 12

VI NOTION DE FACTORISATION On utilise la formule de la distributivité dans l’autre sens kx(a+b) =kxa + kxb Développer Factoriser kxa + kxb = kx(a+b) On met k en facteur commun Ex 1: 5 a + 5 b = 5(a + b) Ex 2: 15 a + 10 b = 5 x 3 a + 5 x 2 b ‘’’’ = 5(3 a + 2 b)

CALCUL LITTERAL Revoir les exercices Apprendre le cours FIN