CHAPITRE 1 Rappels CHAPITRE 1 Rappels 1 2

CHAPITRE 1: Rappels

CHAPITRE 1: Rappels 1. 2 LES OPÉRATIONS ARITHMÉTIQUES 1. 2. 1 Les exposants entiers positifs La puissance kième d’un nombre ou d’une variable.

CHAPITRE 1: Rappels 1. 2 LES OPÉRATIONS ARITHMÉTIQUES 1. 2. 1 Les exposants entiers positifs • Si x > 0, la puissance est toujours positive. • Si x < 0, il faut considérer deux possibilités : 1 o Si k est pair, alors > 0 ex: 2 o Si k est pair, alors >0 ex:

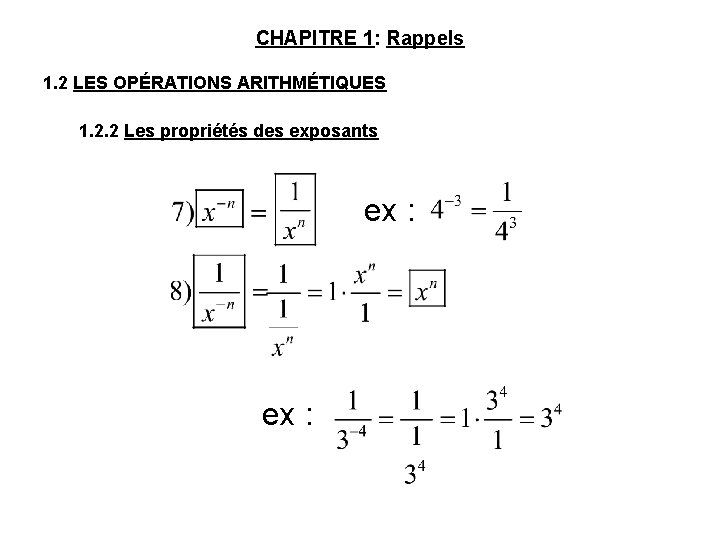
CHAPITRE 1: Rappels 1. 2 LES OPÉRATIONS ARITHMÉTIQUES 1. 2. 2 Les propriétés des exposants • Soit Alors : ex :

CHAPITRE 1: Rappels 1. 2 LES OPÉRATIONS ARITHMÉTIQUES 1. 2. 2 Les propriétés des exposants ex :

CHAPITRE 1: Rappels 1. 2 LES OPÉRATIONS ARITHMÉTIQUES 1. 2. 2 Les propriétés des exposants (voir 3) ex :

CHAPITRE 1: Rappels 1. 2 LES OPÉRATIONS ARITHMÉTIQUES 1. 2. 2 Les propriétés des exposants ex :

CHAPITRE 1: Rappels 1. 2 LES OPÉRATIONS ARITHMÉTIQUES 1. 2. 2 Les propriétés des exposants ex :

CHAPITRE 1: Rappels 1. 2 LES OPÉRATIONS ARITHMÉTIQUES 1. 2. 2 Les propriétés des exposants ex :

CHAPITRE 1: Rappels 1. 2 LES OPÉRATIONS ARITHMÉTIQUES 1. 2. 2 Les propriétés des exposants ex :

CHAPITRE 1: Rappels 1. 3 LES RACINES ET LES EXPOSANTS FRACTIONNAIRES • Une fonction racine carrée est une fonction dont la règle de correspondance est de la forme où y est la racine carrée POSITIVE de x.

CHAPITRE 1: Rappels 1. 3 LES RACINES ET LES EXPOSANTS FRACTIONNAIRES • Il y a une grande différence entre évaluer une racine et résoudre une équation. • • Équation • alors =_______ Ne peut être à la fois négatif et positif car ce ne serait plus une fonction. =_______

CHAPITRE 1: Rappels 1. 3 LES RACINES ET LES EXPOSANTS FRACTIONNAIRES • Exemples : Évaluer les nombres suivants:

CHAPITRE 1: Rappels 1. 3 LES RACINES ET LES EXPOSANTS FRACTIONNAIRES • Remarques:

CHAPITRE 1: Rappels 1. 3 LES RACINES ET LES EXPOSANTS FRACTIONNAIRES • Exemples : Transformer chacune des expressions suivantes: Radical vers exposant ou exposant vers radical.

CHAPITRE 1: Rappels 1. 3 LES RACINES ET LES EXPOSANTS FRACTIONNAIRES

CHAPITRE 1: Rappels 1. 3 LES RACINES ET LES EXPOSANTS FRACTIONNAIRES • Remarques: Si chacune des racines n-ième existe: (car une racine est un exposant)

CHAPITRE 1: Rappels 1. 3 LES RACINES ET LES EXPOSANTS FRACTIONNAIRES • Exemples : Simplifier chacune des expressions suivantes:

6. 2. 4 LA RATIONALISATION D’UN DÉNOMINATEUR Lorsqu’une fraction comporte une racine carrée au dénominateur, il peut être avantageux de la transformer en une expression équivalente dont le dénominateur ne comprend plus de radical. Pour ce faire, nous devons multiplier le numérateur et le dénominateur par une expression dont la forme dépend de celle du dénominateur. Si le dénominateur d’une fraction algébrique est un multiple d’une racine carrée, nous devons multiplier le numérateur et le dénominateur de la fraction par cette racine.

6. 2. 4 LA RATIONALISATION D’UN DÉNOMINATEUR Exemples : Rationnaliser le dénominateur de chacune des expressions suivantes. Remarque : Dans ce cas, nous utilisons la définition de la racine carrée selon laquelle

6. 2. 4 LA RATIONALISATION D’UN DÉNOMINATEUR Si le dénominateur est la somme de deux termes dont au moins un est une racine carrée, nous devons rationaliser cette expression en multipliant le numérateur et le dénominateur de la fraction par le conjugué ___________ du dénominateur, changeant le signe c’est-à-dire l’expression obtenu en _____________ de son deuxième terme. est le conjugué de________________.

6. 2. 4 LA RATIONALISATION D’UN DÉNOMINATEUR Remarque : Dans ce cas, nous utilisons la définition de la racine carrée selon laquelle Preuve:

6. 2. 4 LA RATIONALISATION D’UN DÉNOMINATEUR Exemples : Rationnaliser le dénominateur de chacune des fractions suivantes.

CHAPITRE 1: Rappels 1. 5 LA FACTORISATION DES POLYNÔMES 1. 5. 3 Techniques de factorisation (les plus générales) 1° Mise en évidence simple (La première étape à essayer lorsqu’on veut factoriser !!) On utilise cette méthode lorsque tous les termes contiennent un facteur commun. Ce facteur commun est mis en évidence en utilisant la propriété de la distribution de la multiplication sur l’addition.

CHAPITRE 1: Rappels 1. 5 LA FACTORISATION DES POLYNÔMES 1. 5. 3 Techniques de factorisation Remarque : À moins d’indication contraire, la quantité mise en évidence correspond au PGCD des termes de l’expression. (On met toujours en évidence le plus grand terme possible!)

CHAPITRE 1: Rappels 1. 5 LA FACTORISATION DES POLYNÔMES 1. 5. 3 Techniques de factorisation • Exemples :

CHAPITRE 1: Rappels 1. 5 LA FACTORISATION DES POLYNÔMES 1. 5. 3 Techniques de factorisation

CHAPITRE 1: Rappels 1. 5 LA FACTORISATION DES POLYNÔMES 1. 5. 3 Techniques de factorisation 2° Double mise en évidence On utilise cette méthode lorsqu’il n’existe pas de facteur commun à tous les termes, mais en regroupant les termes par deux (ou par trois), chaque pair (ou triplet) contient un facteur commun. Après les avoir regroupés, on effectue deux mises en évidence simple successives, si possible.

CHAPITRE 1: Rappels 1. 5 LA FACTORISATION DES POLYNÔMES 1. 5. 3 Techniques de factorisation

CHAPITRE 1: Rappels 1. 5 LA FACTORISATION DES POLYNÔMES 1. 5. 3 Techniques de factorisation • Exemples :

CHAPITRE 1: LES BASES DE L’ALGÈBRE 1. 5 LA FACTORISATION DES POLYNÔMES 1. 5. 3 Techniques de factorisation

CHAPITRE 1: Rappels 1. 5 LA FACTORISATION DES POLYNÔMES 1. 5. 3 Techniques de factorisation 3° Trinôme général avec Soit une expression de la forme Si , pour factoriser un tel trinôme: 1 - On cherche deux nombres entier m et n dont la somme est b et le produit de ac. S: P:

CHAPITRE 1: Rappels 1. 5 LA FACTORISATION DES POLYNÔMES 1. 5. 3 Techniques de factorisation Remarque: Si P > 0, alors les nombres cherchés m et n sont le même signe. Si P < 0, alors les nombres cherchés m et n sont de signe opposé.

CHAPITRE 1: Rappels 1. 5 LA FACTORISATION DES POLYNÔMES 1. 5. 3 Techniques de factorisation 2 - On remplace b par la somme de ces deux nombres, m et n. 3 - On effectue une double mise en évidence.

CHAPITRE 1: Rappels 1. 5 LA FACTORISATION DES POLYNÔMES 1. 5. 3 Techniques de factorisation • Exemples :

CHAPITRE 1: Rappels 1. 5 LA FACTORISATION DES POLYNÔMES 1. 5. 3 Techniques de factorisation

CHAPITRE 1: Rappels 1. 5 LA FACTORISATION DES POLYNÔMES 1. 5. 3 Techniques de factorisation 4° Trinôme général avec Soit une expression de la forme Si , pour factoriser un tel trinôme: La procédure est semblable à 4° sauf pour l’étape 2 :

CHAPITRE 1: Rappels 1. 5 LA FACTORISATION DES POLYNÔMES 1. 5. 3 Techniques de factorisation 2 - On remplace b par la somme de ces deux nombres, m et n.

CHAPITRE 1: Rappels 1. 5 LA FACTORISATION DES POLYNÔMES 1. 5. 3 Techniques de factorisation • Exemples :

CHAPITRE 1: Rappels 1. 5 LA FACTORISATION DES POLYNÔMES 1. 5. 3 Techniques de factorisation * Il y a donc moins d’étapes que si .

CHAPITRE 1: Rappels 1. 5 LA FACTORISATION DES POLYNÔMES 1. 5. 3 Techniques de factorisation N. B. : Il n’est pas toujours possible de trouver deux valeurs entières dont la somme est b et le produit est c. Dans ce cas, la factorisation est impossible du trinôme où les coefficients de ses facteurs ne sont des entiers. On peut dans ce cas utiliser la formule quadratique:

CHAPITRE 1: Rappels 1. 5 LA FACTORISATION DES POLYNÔMES 1. 5. 3 Techniques de factorisation 5° Différence de deux carrés On utilise cette méthode pour factoriser un binôme composé de la différence de deux carrés. Il peut s’exprimer comme le produit de la somme et la différence des deux racines carrés. car les termes en x s’annulent

CHAPITRE 1: Rappels 1. 5 LA FACTORISATION DES POLYNÔMES 1. 5. 3 Techniques de factorisation • Exemples :

CHAPITRE 1: Rappels 1. 5 LA FACTORISATION DES POLYNÔMES 1. 5. 3 Techniques de factorisation Somme de deux carrés Un somme de deux carrés ne se factorise pas (du moins avec une nouvelle méthode). Exemple : ATTENTION !!!

CHAPITRE 1: LES BASES DE L’ALGÈBRE 1. 7 LA FACTORISATION DES POLYNÔMES 1. 7. 2 Techniques de factorisation 6° Somme ou différence de deux cubes On utilise cette méthode pour factorise un binôme dont chacun des termes est le cube d’un nombre ou d’une expression algébrique.

CHAPITRE 1: LES BASES DE L’ALGÈBRE 1. 7 LA FACTORISATION DES POLYNÔMES 1. 7. 2 Techniques de factorisation Lorsqu’on sait que est un facteur de ou lorsqu’on sait que facteur de est un , l’autre facteur est trouvé en effectuant le quotient des polynômes, ou .

CHAPITRE 1: LES BASES DE L’ALGÈBRE 1. 7 LA FACTORISATION DES POLYNÔMES 1. 7. 2 Techniques de factorisation • Exemples :

CHAPITRE 1: LES BASES DE L’ALGÈBRE 1. 7 LA FACTORISATION DES POLYNÔMES 1. 7. 2 Techniques de factorisation • En posant comme facteur du polynôme, on peut obtenir l’autre facteur en divisant:

CHAPITRE 1: LES BASES DE L’ALGÈBRE (SUITE…) 1. 6 LES OPÉRATIONS SUR LES POLYNÔMES 1. 6. 6 Le quotient de polynômes

CHAPITRE 1: LES BASES DE L’ALGÈBRE 1. 7 LA FACTORISATION DES POLYNÔMES 1. 7. 2 Techniques de factorisation Remarque: Un polynôme peut souvent se décomposer en plus de deux facteurs. Il s’agit d’abord d’effectuer la mise en évidences simple pour découvrir un autre polynôme dont on reconnaît le modèle. L’habileté à factoriser des polynômes s’acquiert par LA PRATIQUE !!!

La résolution d’une équation Trouver les valeurs de x qui respectent l’équation.

La résolution d’une équation Ex: Résoudre l’équation suivante