Ch 19 Electric Potential Energy and the Electric

Ch. 19: Electric Potential Energy and the Electric Potential. • • Early History Applications Related equations Capacitor Networks 2/28/2021 LNK 2 LRN 1

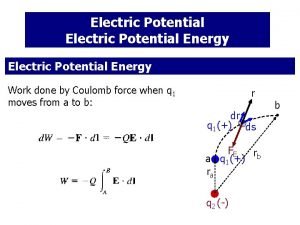
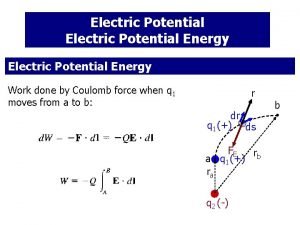
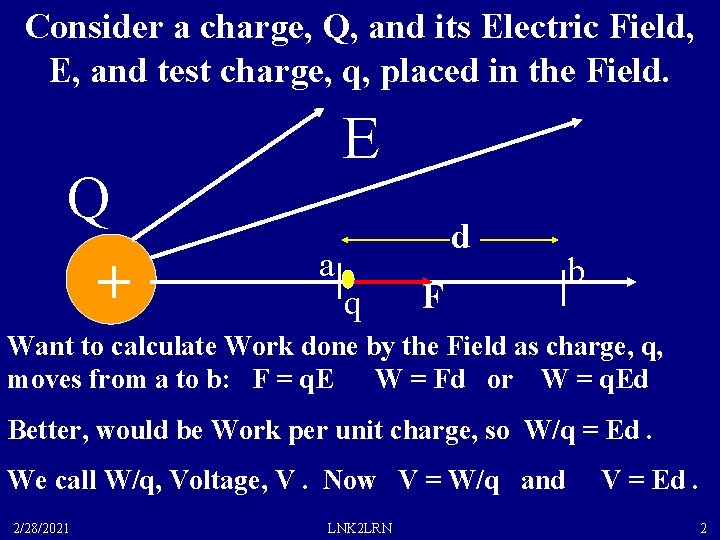
Consider a charge, Q, and its Electric Field, E, and test charge, q, placed in the Field. Q + E a| q d F b | Want to calculate Work done by the Field as charge, q, moves from a to b: F = q. E W = Fd or W = q. Ed Better, would be Work per unit charge, so W/q = Ed. We call W/q, Voltage, V. Now V = W/q and V = Ed. 2/28/2021 LNK 2 LRN 2

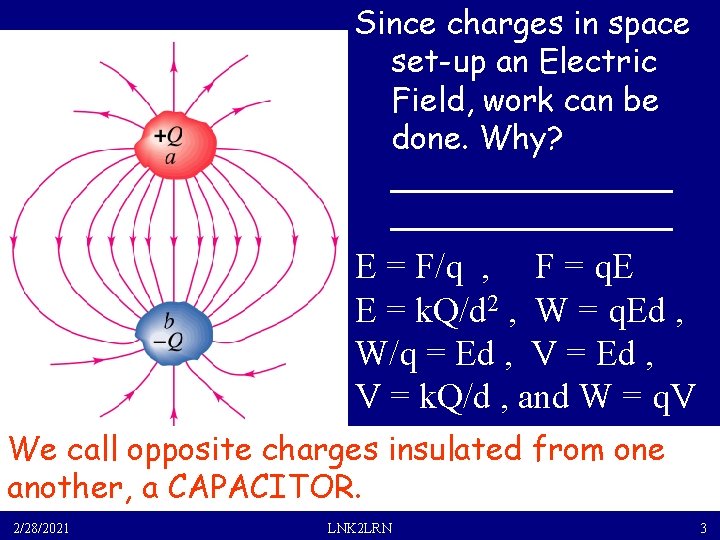
Since charges in space set-up an Electric Field, work can be done. Why? ______________ E = F/q , F = q. E E = k. Q/d 2 , W = q. Ed , W/q = Ed , V = Ed , V = k. Q/d , and W = q. V We call opposite charges insulated from one another, a CAPACITOR. 2/28/2021 LNK 2 LRN 3

Early History of Capacitors. Galvanism: Published in 1790, how electrical current was produced from the contact of two different metals in a moist environment. Luigi Galvani (1737 -1798) Frog-leg “I have learned more from my mistakes than experiment. from my successes. ” 2/28/2021 LNK 2 LRN 4

In 1799, metal discs (zinc with copper or silver) , separated with paperboard discs Alessandro Giuseppe Volta soaked in saline solution. This stack (1745 -1827) was the first electric The Voltaic Pile. battery. “Perhaps too much to expect one to be both the prince of experimentalists and a competent mathematician. ” 2/28/2021 LNK 2 LRN 5

In 1810, Davy uses the Voltaic Pile to begin Electrochemistry. Isolated elemental K, Na, B, Ca, Sr, B, Si, and Mg. Many consider Davy the greatest Chemist. “Man cannot discover new oceans unless he has the courage to lose sight of the shore. ” 2/28/2021 Sir Humphry Davy (1778 -1829) Electrochemistry. LNK 2 LRN 6

Michael Faraday (1791 -1867) discovered variable capacitor. Later, the SI unit used for capacitance was named a Farad (F) in his honor. 1 F = 1 C / V In words: one Farad is equal to one Coulomb per Volt Upon his knighthood, “Ask her to wait a moment - I am almost done with my work. ” 2/28/2021 LNK 2 LRN 7

Capacitance • Capacitance is the ability of a conductor to store energy in the form of electrically separated charges. 2/28/2021 LNK 2 LRN 8

Capacitors 2/28/2021 LNK 2 LRN 9

Capacitance • Capacitance is the ratio of charge to potential difference (voltage). Q C = ΔV 2/28/2021 LNK 2 LRN 10

Farads • Capacitance is measured in units called Farads (F). • 1 Farad = 1 Coulomb / 1 Volt • Common measures are in microfarads (m. F) and picofarads (p. F = 1 x 10 -12 F). • Named for Michael Faraday (17911867), the prominent British physicist of the 1800’s. 2/28/2021 LNK 2 LRN 11

Capacitance depends on: • Size and shape of capacitor. • Material between the plates. A C = εo d 2/28/2021 LNK 2 LRN 12

Permittivity of free space: The Greek letter epsilon, e, represents a material-dependent constant called the permittivity of the material. When it is followed by a subscripted o, it is called the permittivity of free space, and has a value of 8. 85 x 10 -12 C 2/N. m 2 2/28/2021 LNK 2 LRN 13

Energy stored in a capacitor: From research, we get the equation Stored Energy, U. equals the ability to do Work, W = ½ QV And using C = Q / V, we get W = Q 2 / 2 C = ½ C V 2 = ½ Q V 2/28/2021 LNK 2 LRN 14

Capacitors are used for several purposes: • Timing - controlling the charging and discharging of flashing lights. • Smoothing - converting AC to DC. • Coupling - between stages of an audio system and to connect a loudspeaker. • Filtering - in the tone control of an audio system. • Tuning - in a radio system. • Storing energy - in a camera flash circuit. 2/28/2021 LNK 2 LRN 15

Capacitance Example How much charge is on a 1 F capacitor which has a potential difference of 110 Volts? Q = CV = (1 F )(110 V) = 110 Coulombs How much energy is stored in this capacitor? W = ½QV = ½(110 C) (110 V) = 6, 050 Joules! 2/28/2021 LNK 2 LRN 16

Parallel Plate Capacitor Example C = e 0 A/d Calculate the capacitance of a parallel plate capacitor made from two large square metal sheets 1. 3 m on a side, separated by 0. 1 m. A A d 2/28/2021 LNK 2 LRN 17

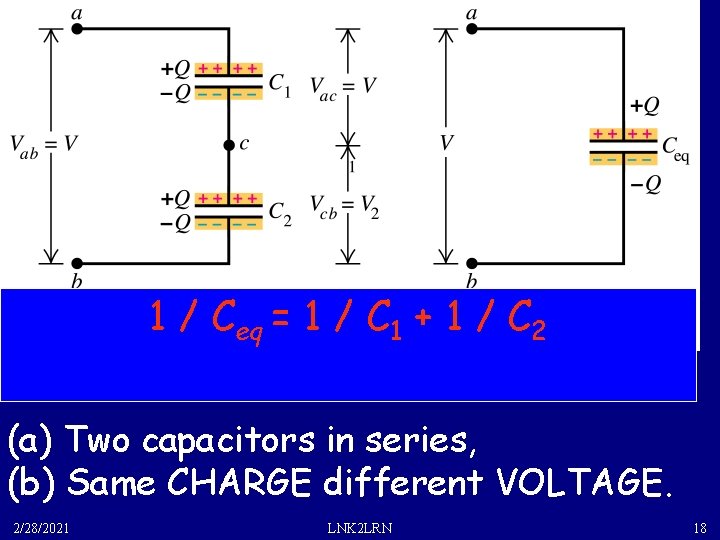
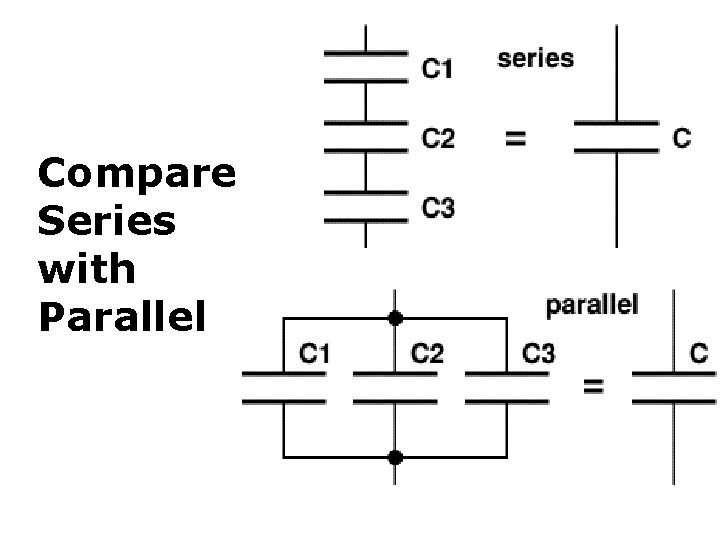
1 / Ceq = 1 / C 1 + 1 / C 2 (a) Two capacitors in series, (b) Same CHARGE different VOLTAGE. 2/28/2021 LNK 2 LRN 18

Ceq = C 1 + C 2 + C 3 ··· Cn (a) Capacitors in parallel, (b) Same VOLTAGE different CHARGE. 2/28/2021 LNK 2 LRN 19

Compare Series with Parallel 2/28/2021 LNK 2 LRN 20

Dielectric • Placing a dielectric between the plates increases the capacitance. Dielectric constant (kappa) (k > 1) • C = k C 0 Capacitance without dielectric Capacitance with dielectric 2/28/2021 LNK 2 LRN 21

Dielectric Constant, Strength • Large capacitance (energy storage) – Small gap (d) • Breakdown voltage is material dependent – Large area (A) • Would like to keep the device size tolerable – Large dielectric constant (ke 0) • Large dielectric strength Dielectric constant and strength of material C = k εo 2/28/2021 Material Constant k Strength (V/m) Vacuum 1. 00000 - Air 1. 00059 3 x 106 Paper 3. 7 16 x 106 Mica 5. 4 50 x 106 LNK 2 LRN A d 22

Capacitors can store charge and ENERGY DU = q DV, and the potential V increases as the charge is placed on the plates (V = Q / C). Since the V changes as the Q is increased, we have to integrate over all the little charges “dq” being added to a plate: DU = q DV leads to U = ò V dq = ò q/c dq = 1/C ò q dq = Q 2 / 2 C. And using Q = C V, we get U = Q 2 / 2 C = C V 2 / 2 = Q V / 2 So the energy stored in a capacitor can be thought of as the potential energy stored in the system of positive charges that are separated from the negative charges, much like a stretched 2/28/2021 LNK 2 LRN associated with it. 23 spring has potential energy

ELECTRIC FIELD ENERGY Here's another way to think of the energy stored in a charged capacitor: If we consider the space between the plates to contain the energy (equal to 1/2 C V 2) we can calculate an energy DENSITY (Joules per volume). The volume between the plates is area x plate separation, or A d. Then the energy density u is u = 1/2 C V 2 / A d = eo E 2 / 2 Recall C = eo A / d and V =E d. 2/28/2021 LNK 2 LRN 24

Energy density: u = eo E 2 / 2 This is an important result because it tells us that empty space contains energy if there is an electric field (E) in the "empty" space. If we can get an electric field to travel (or propagate) we can send or transmit energy and information through empty space!!! 2/28/2021 LNK 2 LRN 25