Electric Potential Electrostatic Potential Energy and Potential Difference





















- Slides: 32

Electric Potential

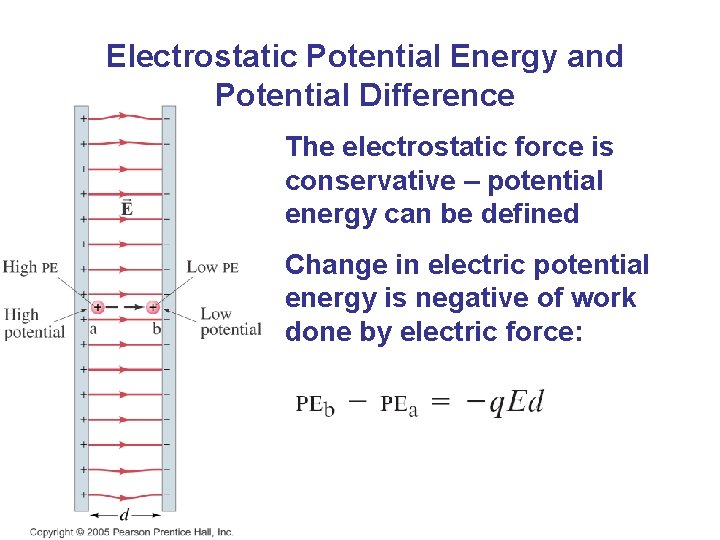
Electrostatic Potential Energy and Potential Difference The electrostatic force is conservative – potential energy can be defined Change in electric potential energy is negative of work done by electric force:

Electrostatic Potential Energy and Potential Difference Electric potential is defined as potential energy per unit charge: Unit of electric potential: the volt (V). 1 V = I J/C.

Electrostatic Potential Energy and Potential Difference Only changes in potential can be measured, allowing free assignment of V = 0.

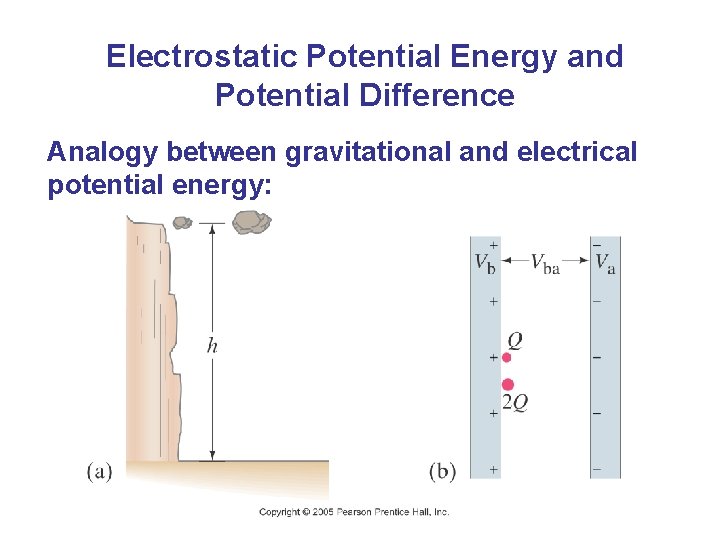
Electrostatic Potential Energy and Potential Difference Analogy between gravitational and electrical potential energy:

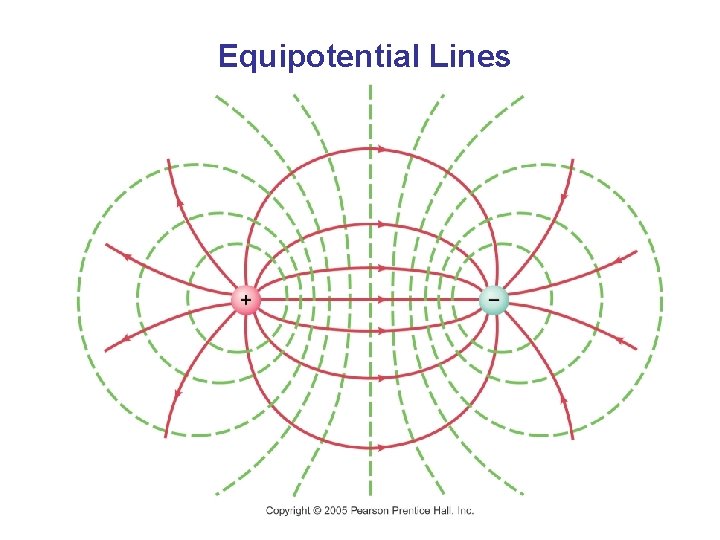
Equipotential Lines An equipotential is a line or surface over which the potential is constant. Electric field lines are perpendicular to equipotentials. The surface of a conductor is an equipotential.

Equipotential Lines

The Electron Volt, a Unit of Energy One electron volt (e. V) is the energy gained by an electron moving through a potential difference of one volt.

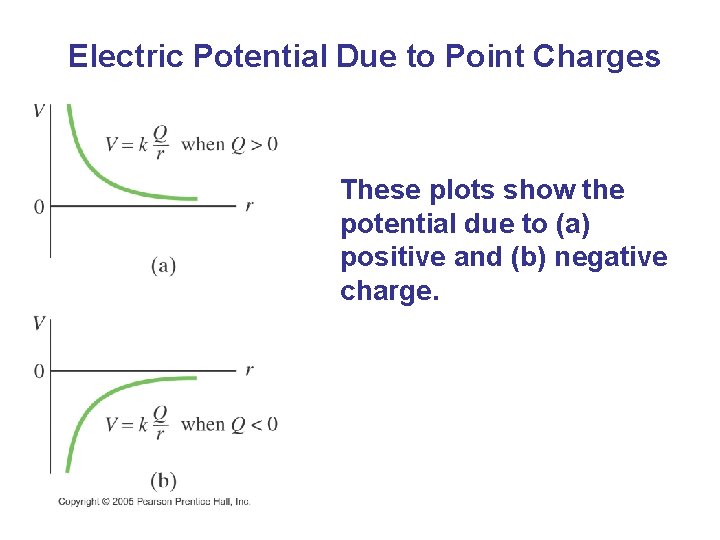
Electric Potential Due to Point Charges The electric potential due to a point charge can be derived:

Electric Potential Due to Point Charges These plots show the potential due to (a) positive and (b) negative charge.

Electric Potential Due to Point Charges Using potentials instead of fields can make solving problems much easier – potential is a scalar quantity, whereas the field is a vector.

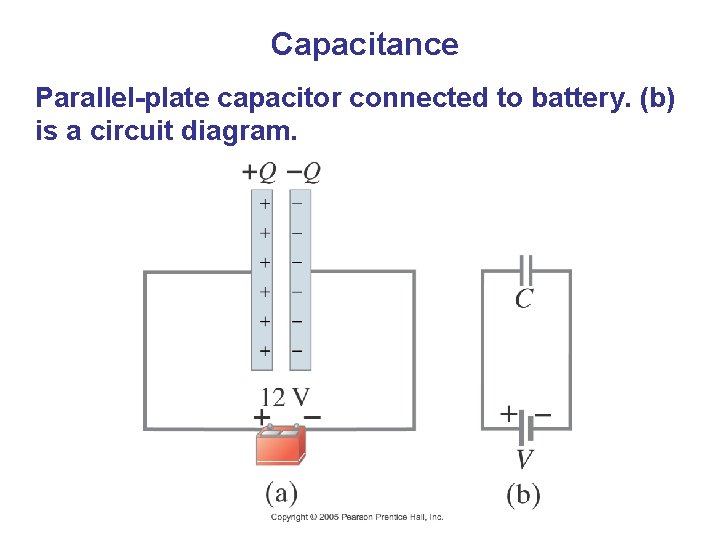
Capacitance A capacitor consists of two conductors that are close but not touching. A capacitor has the ability to store electric charge.

Capacitance Parallel-plate capacitor connected to battery. (b) is a circuit diagram.

Capacitance When a capacitor is connected to a battery, the charge on its plates is proportional to the voltage: The quantity C is called the capacitance. Unit of capacitance: the farad (F) 1 F = 1 C/V

Capacitance The capacitance does not depend on the voltage; it is a function of the geometry and materials of the capacitor. For a parallel-plate capacitor:

A parallel–plate capacitor has a capacitance Co. A second parallel–plate capacitor has plates with twice the area and twice the separation. The capacitance of the second capacitor is most nearly (A) ¼Co (B) ½Co (C) Co (D) 2 Co (E) 4 Co

A parallel–plate capacitor has a capacitance Co. A second parallel–plate capacitor has plates with twice the area and twice the separation. The capacitance of the second capacitor is most nearly (A) ¼Co (B) ½Co (C) Co (D) 2 Co (E) 4 Co

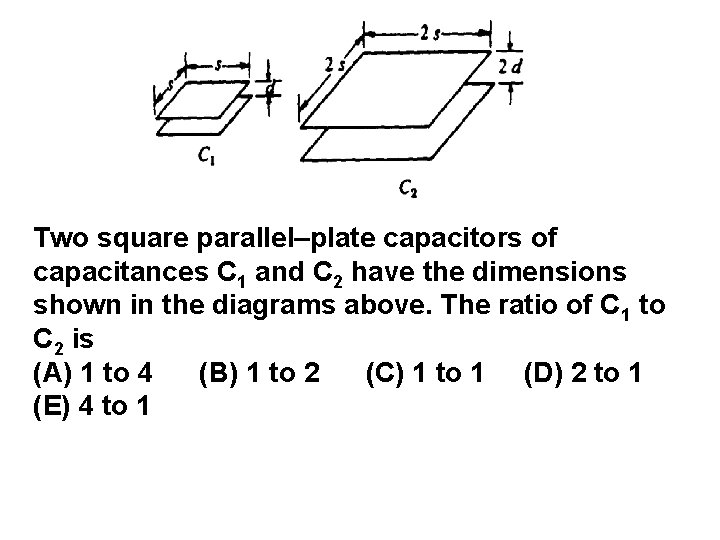
Two square parallel–plate capacitors of capacitances C 1 and C 2 have the dimensions shown in the diagrams above. The ratio of C 1 to C 2 is (A) 1 to 4 (B) 1 to 2 (C) 1 to 1 (D) 2 to 1 (E) 4 to 1

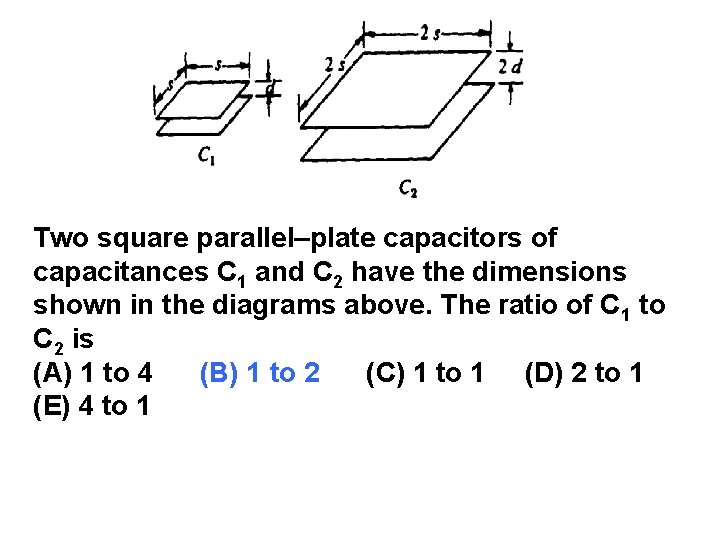
Two square parallel–plate capacitors of capacitances C 1 and C 2 have the dimensions shown in the diagrams above. The ratio of C 1 to C 2 is (A) 1 to 4 (B) 1 to 2 (C) 1 to 1 (D) 2 to 1 (E) 4 to 1

Dielectrics A dielectric is an insulator, and is characterized by a dielectric constant K. Capacitance of a parallel-plate capacitor filled with dielectric:

Dielectrics Dielectric strength is the maximum field a dielectric can experience without breaking down.

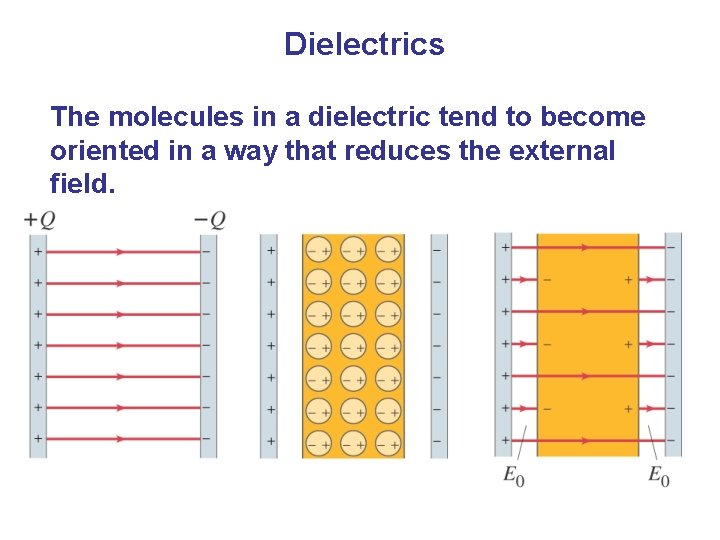
Dielectrics The molecules in a dielectric tend to become oriented in a way that reduces the external field.

Dielectrics This means that the electric field within the dielectric is less than it would be in air, allowing more charge to be stored for the same potential.

A sheet of mica is inserted between the plates of an isolated charged parallel–plate capacitor. Which of the following statements is true? (A)The capacitance decreases. (B) The potential difference across the capacitor decreases. (C) The energy of the capacitor does not change. (D) The charge on the capacitor plates decreases (E) The electric field between the capacitor plates increases.

A sheet of mica is inserted between the plates of an isolated charged parallel–plate capacitor. Which of the following statements is true? (A)The capacitance decreases. (B) The potential difference across the capacitor decreases. (C) The energy of the capacitor does not change. (D) The charge on the capacitor plates decreases (E) The electric field between the capacitor plates increases. Since the capacitor is isolated, Q remains constant. Filling the place with oil (a dielectric) will increase the capacitance, causing the potential (V = Q/C) to decrease.

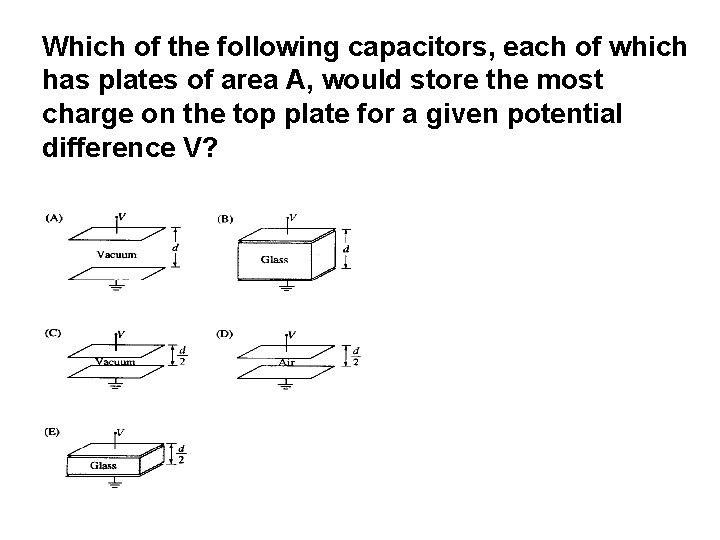
Which of the following capacitors, each of which has plates of area A, would store the most charge on the top plate for a given potential difference V?

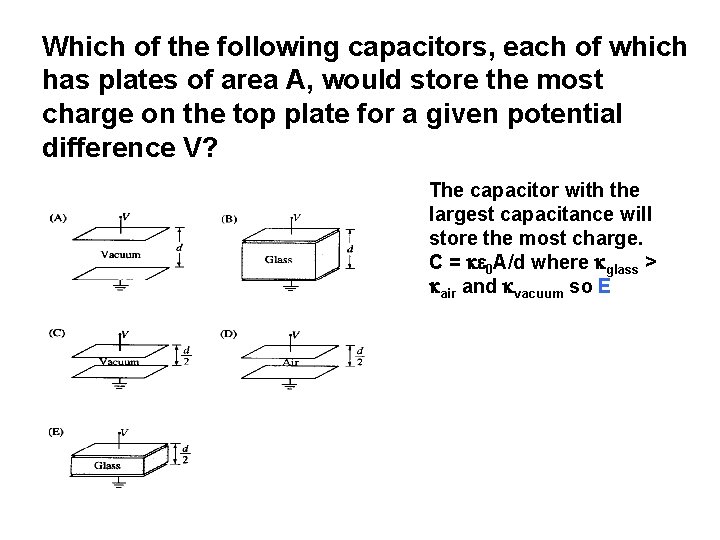
Which of the following capacitors, each of which has plates of area A, would store the most charge on the top plate for a given potential difference V? The capacitor with the largest capacitance will store the most charge. C = 0 A/d where glass > air and vacuum so E

Storage of Electric Energy A charged capacitor stores electric energy; the energy stored is equal to the work done to charge the capacitor.

A 20 μF parallel–plate capacitor is fully charged to 30 V. The energy stored in the capacitor is most nearly (A)9 × 103 J (B) 9 × 10– 3 J (C) 6 × 10– 4 J (D) 2 × 10– 4 J (E) 2 × 10– 7 J

A 20 μF parallel–plate capacitor is fully charged to 30 V. The energy stored in the capacitor is most nearly (A)9 × 103 J (B) 9 × 10– 3 J (C) 6 × 10– 4 J (D) 2 × 10– 4 J (E) 2 × 10– 7 J UC = ½ CV 2

A potential difference V is maintained between two large, parallel conducting plates. An electron starts from rest on the surface of one plate and accelerates toward the other. Its speed as it reaches the second plate is proportional to (A) 1/V (B) (C) √V (D) V (E) V 2

A potential difference V is maintained between two large, parallel conducting plates. An electron starts from rest on the surface of one plate and accelerates toward the other. Its speed as it reaches the second plate is proportional to (A) 1/V (B) (C) √V (D) V (E) V 2 W = K = q V and K = ½ mv 2