Automata Grammars and Languages Discourse 02 Preliminaries C

Automata, Grammars and Languages Discourse 02 Preliminaries C SC 473 Automata, Grammars & Languages

Sets • Set: primitive notion of “aggregate”—from which all of mathematics and logic can be constructed • One small hierarchy of concepts in this course: derives Grammar real sequence string function rational relation integer tuple set C SC 473 Automata, Grammars & Languages 2

Sets (cont’d) • Predicate P(x): a statement about a variable x that is true or false when x is replaced by a particular object n n P(x) = x is odd Main predicate for set-membership: “x A” • Some axioms of set theory n n Axiom of Extension: a set is determined by its “extension”: Axiom of Specification: For every set A and predicate P(x) there is a set of all elements of A for which P is true. • Ex: {x Z: x is positive and not prime} = {4, 6, 8, 9, 10, 12, …} C SC 473 Automata, Grammars & Languages 3

Sets (cont’d) • Operations and relations on sets n n n n subset proper subset union intersection complement difference size of set • Special sets n empty set natural numbers integers n n • Sets of sets n Power set C SC 473 Automata, Grammars & Languages 4

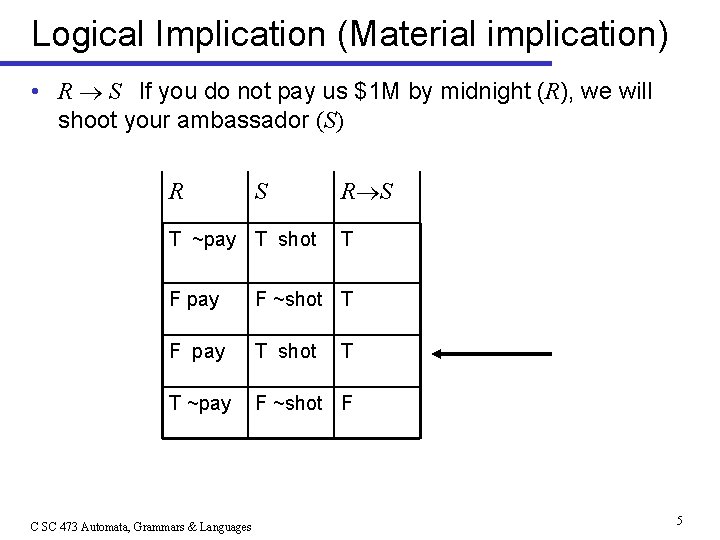
Logical Implication (Material implication) • R S If you do not pay us $1 M by midnight (R), we will shoot your ambassador (S) R S T ~pay T shot R S T F pay F ~shot T F pay T shot T ~pay F ~shot F C SC 473 Automata, Grammars & Languages T 5

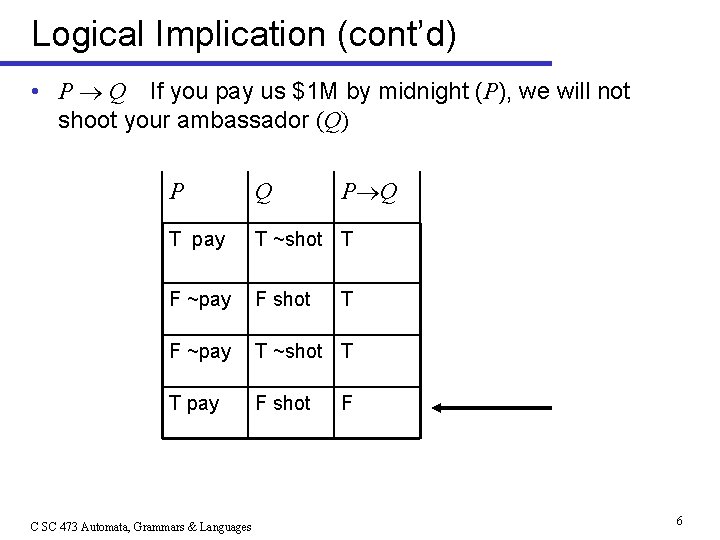
Logical Implication (cont’d) • P Q If you pay us $1 M by midnight (P), we will not shoot your ambassador (Q) P Q T pay T ~shot T F ~pay F shot F ~pay T ~shot T T pay F shot C SC 473 Automata, Grammars & Languages P Q T F 6

Quantifiers • • • Ex: defining “big Oh” relationship between functions • Ex: continuity of a function at a point (“epsilon-delta defn”) • Abe Lincoln’s quote canfool(p, t) = can fool person p at time t C SC 473 Automata, Grammars & Languages 7

Quantifiers (cont’d) • Relationship between and • Ex: “cannot fool all of the people all of the time” • Ex: non-continuity at a point C SC 473 Automata, Grammars & Languages 8

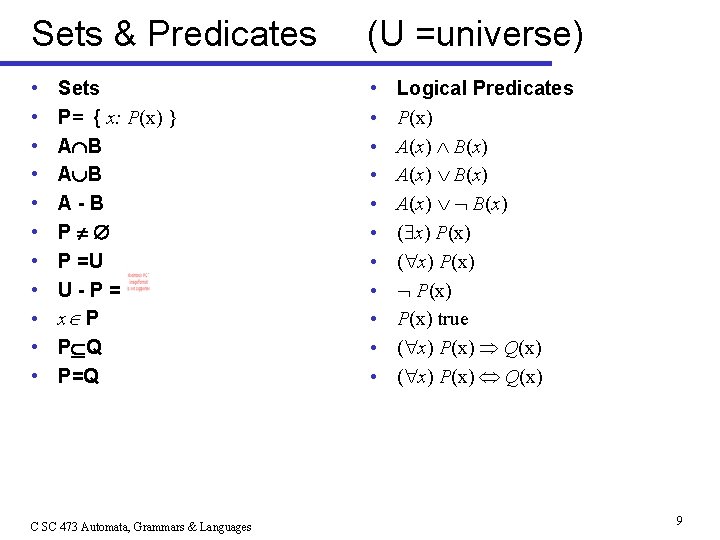
Sets & Predicates (U =universe) • • • • • • Sets P= { x: P(x) } A B A-B P P =U U-P= x P P Q P=Q C SC 473 Automata, Grammars & Languages Logical Predicates P(x) A(x) B(x) A(x) B(x) ( x) P(x) true ( x) P(x) Q(x) 9

Tuples • • {3, 7} unordered pair; 2 -tuple (3, 7) ordered pair (3, 7) {{3, 7}, 3} (7, 3) {{3, 7} Generalize to n-tuple: (a 1, a 2, a 3, …, an) Defn. Cartesian Product A x B { (a, b) : a A b B } • Generalization: A 1 x A 2 x … x An C SC 473 Automata, Grammars & Languages 10

Binary Relations • Defn: a binary relation R from A to B is a subset of A B: • Defn: a function f from A to B, written f : A B, is a relation f A B that is single-valued, i. e. , • Defn: one-to-one (injection), onto (surjection), one-to-one correspondence (bijection) n See Definition 4. 12, p. 175, text. Also see below. C SC 473 Automata, Grammars & Languages 11

Binary Relations: 3 views set (postfix) relation (infix) predicate (prefix) (a, b) R a. Rb R (a, b) (3, 10) < 3 < 10 < (3, 10) (Charles, Andrew) is. Fatherof C SC 473 Automata, Grammars & Languages Charles is. Fatherof Andrew is. Fatherof (Charles, Andrew) 12

Why Relations? Generalize Functions. • Ex: functions • Ex: division with remainder E N N • Ex: circle C R R • Ex: Relational Database • Grammar “derives” relation C SC 473 Automata, Grammars & Languages 13

Relational Calculus S R a b A C SC 473 Automata, Grammars & Languages B c C 14

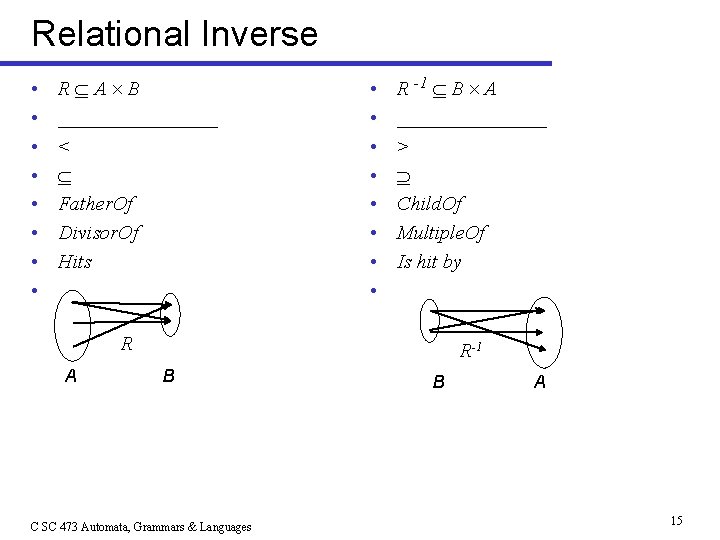
Relational Inverse • • R A B ________ < Father. Of Divisor. Of Hits • • R -1 B A ________ > Child. Of Multiple. Of Is hit by R A R-1 B C SC 473 Automata, Grammars & Languages B A 15

The Calculus • A A • Proposition. If C SC 473 Automata, Grammars & Languages 16

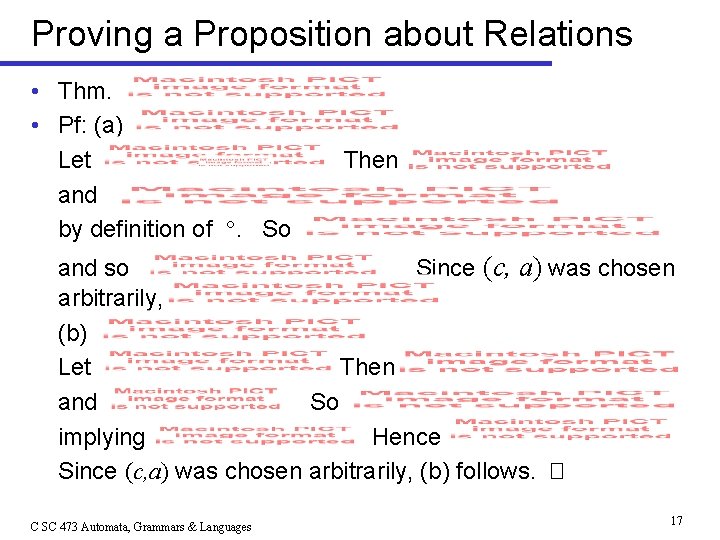
Proving a Proposition about Relations • Thm. • Pf: (a) Let and by definition of . So Then and so Since (c, a) was chosen arbitrarily, (b) Let Then and So implying Hence Since (c, a) was chosen arbitrarily, (b) follows. � C SC 473 Automata, Grammars & Languages 17

Relational Properties R A B Relational calculus C SC 473 Automata, Grammars & Languages predicate calculus name 18

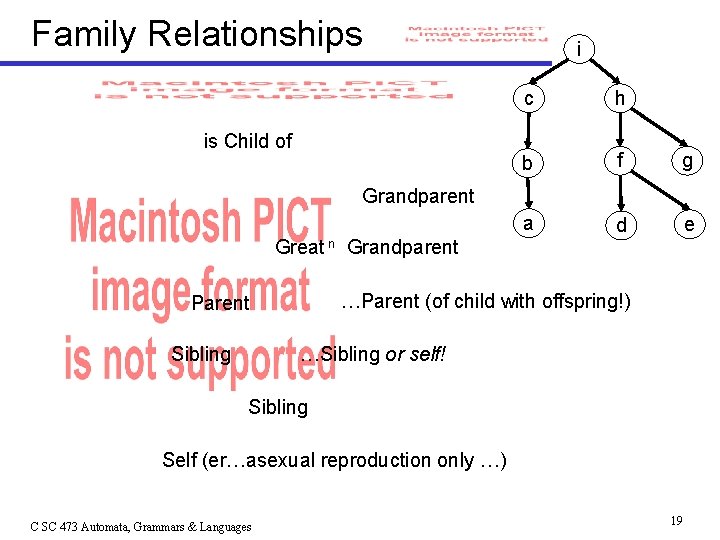
Family Relationships is Child of i c h b f g a d e Grandparent Great n Grandparent …Parent (of child with offspring!) Parent Sibling …Sibling or self! Sibling Self (er…asexual reproduction only …) C SC 473 Automata, Grammars & Languages 19

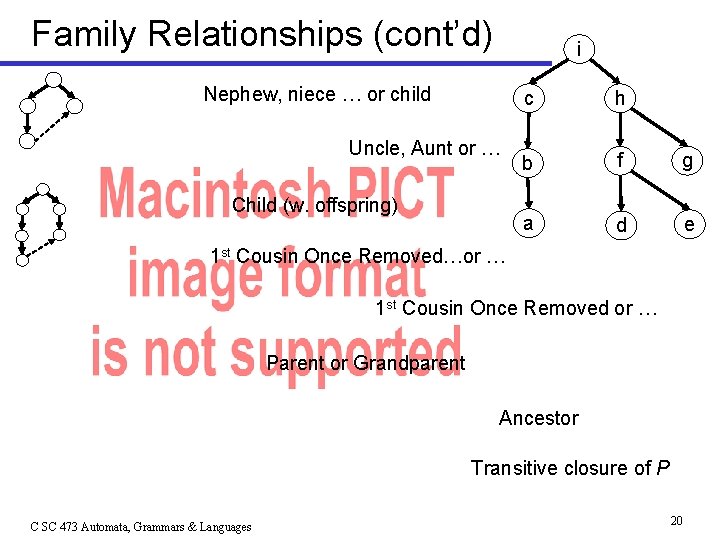
Family Relationships (cont’d) i Nephew, niece … or child Uncle, Aunt or … Child (w. offspring) c h b f g a d e 1 st Cousin Once Removed…or … 1 st Cousin Once Removed or … Parent or Grandparent Ancestor Transitive closure of P C SC 473 Automata, Grammars & Languages 20

Binary Relations on A to itself (A) • Ex: Theorem: C SC 473 Automata, Grammars & Languages 21

Properties of Name R reflexive R symmetric R transitive Defn. R an equivalence relation C SC 473 Automata, Grammars & Languages Relational Calculus reflexive, symmetric & transitive 22

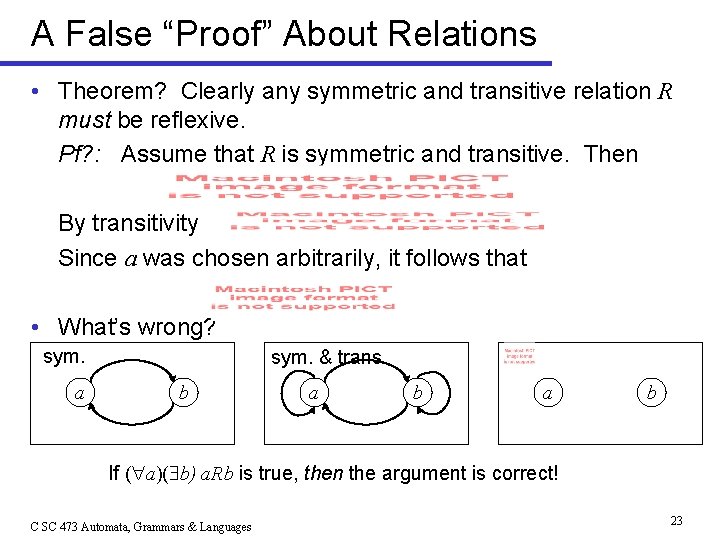
A False “Proof” About Relations • Theorem? Clearly any symmetric and transitive relation R must be reflexive. Pf? : Assume that R is symmetric and transitive. Then By transitivity Since a was chosen arbitrarily, it follows that • What’s wrong? sym. a sym. & trans. b a b If ( a)( b) a. Rb is true, then the argument is correct! C SC 473 Automata, Grammars & Languages 23

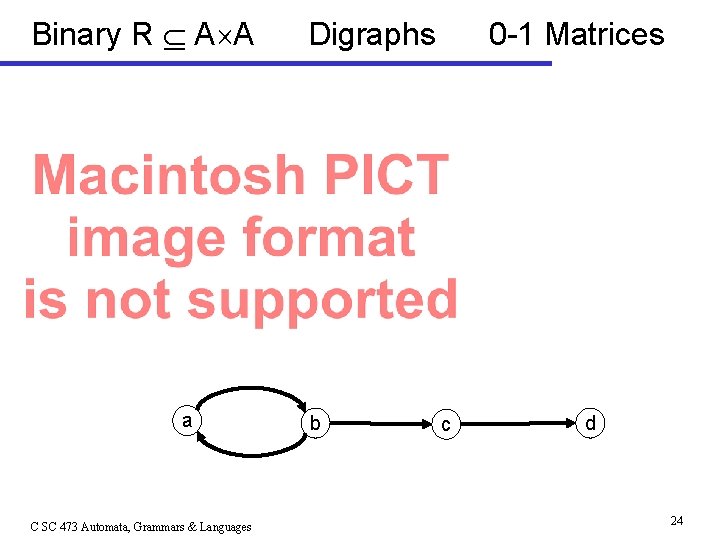
Binary R A A a C SC 473 Automata, Grammars & Languages Digraphs b 0 -1 Matrices c d 24

Binary Relations, Digraphs, Matrices (cont’d) a C SC 473 Automata, Grammars & Languages b c d 25

Binary Relations, Digraphs, Matrices (cont’d) a C SC 473 Automata, Grammars & Languages b c d 26

Binary Relations, Digraphs, Matrices (cont’d) a b d c Repeats! C SC 473 Automata, Grammars & Languages 27

Binary Relations, Digraphs, Matrices (cont’d) a C SC 473 Automata, Grammars & Languages b c d 28

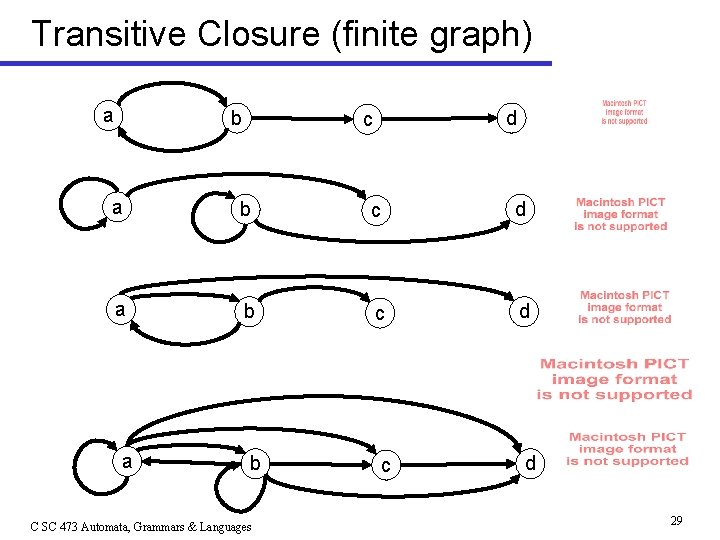
Transitive Closure (finite graph) a b d c a b c d a b C SC 473 Automata, Grammars & Languages c d 29

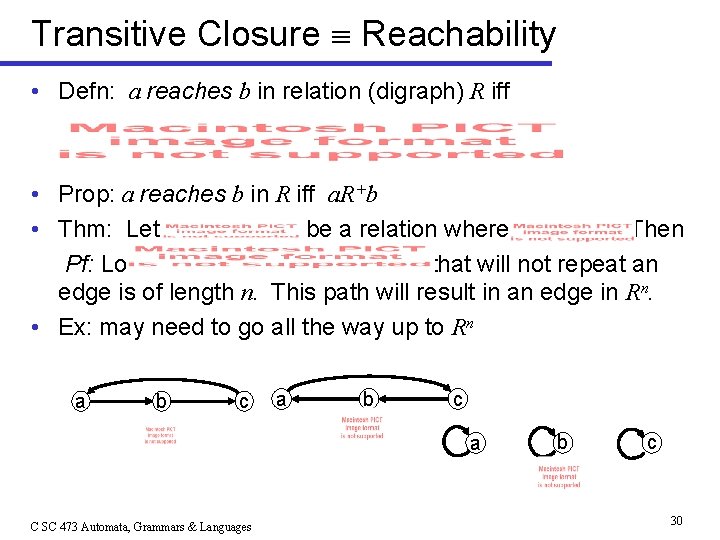
Transitive Closure Reachability • Defn: a reaches b in relation (digraph) R iff • Prop: a reaches b in R iff a. R+b • Thm: Let be a relation where Then Pf: Longest possible path in G(R+) that will not repeat an edge is of length n. This path will result in an edge in Rn. • Ex: may need to go all the way up to Rn a b c a C SC 473 Automata, Grammars & Languages b c 30

Strings and Languages • In this course, a “language” is simply a set of strings; a “programming language” is much more complex • alphabet - a finite set of symbols • String (word) over - finite sequence of symbols • - the empty or null string • |w| - length of string w n What is a string precisely? String w of length n is a function • String ops n n concatenation powers C SC 473 Automata, Grammars & Languages 31

Strings and Languages (cont’d) • = {w: w is a string over } (note: ) • Language L over : a subset L • Ex: = ASCII codes C SC 473 Automata, Grammars & Languages ( = blank = 40 = ) 32

Strings and Languages (cont’d) • Language ops n Set operators n Concatenation n Powers • Ex: C SC 473 Automata, Grammars & Languages 33

Strings and Languages (cont’d) • Language ops (cont’d) n n n Defn: Kleene Closure (Star) Note: Defn: • Ex: C SC 473 Automata, Grammars & Languages 34

Strings and Languages (cont’d) • Theorem: • Pf: • Ex: C SC 473 Automata, Grammars & Languages 35

Strings and Languages (cont’d) • Ex: C SC 473 Automata, Grammars & Languages 36

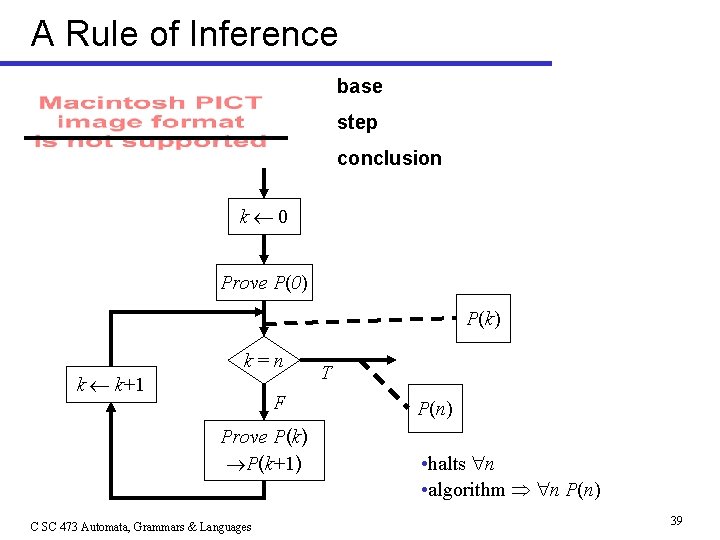
Methods of Proof • Construction: exhibit the object guaranteed by theorem. n Ex: Construction of a regular expression, given a FA. • Contradiction: To show P: Assume P and derive a contraction or clear falsity (“reduction ad absurdum”) n Ex: our proof of undecidability of the halting problem: assumed “halt” program existed and derived an absurd contradiction • Induction: to prove P(n) holds for all non-negative integers n: base (basis) step conclusion C SC 473 Automata, Grammars & Languages 37

Induction C SC 473 Automata, Grammars & Languages 38

A Rule of Inference base step conclusion k 0 Prove P(0) P(k) k k+1 k=n F Prove P(k) P(k+1) C SC 473 Automata, Grammars & Languages T P(n) • halts n • algorithm n P(n) 39

Kinds of Induction • Simple induction _________ • Equivalent _______________ • “Course-of-Values” Induction __________ C SC 473 Automata, Grammars & Languages 40

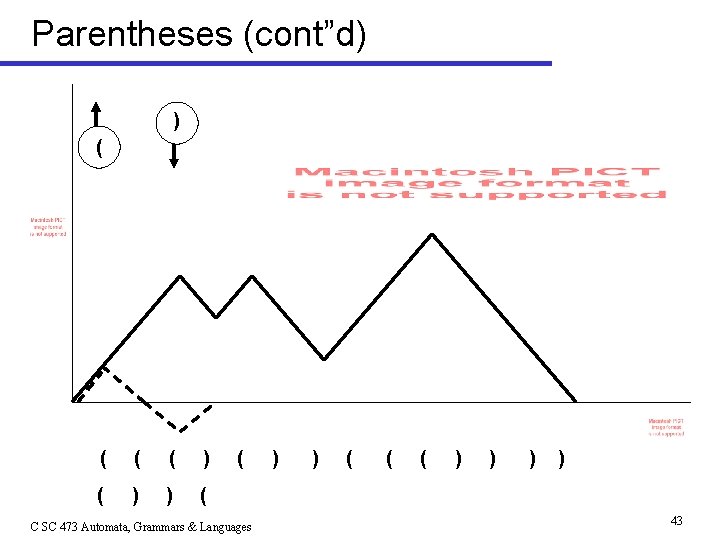
Ex: Induction Argument: Balanced Parens • Defn: The strings having balanced parentheses over {(, )} are defined (inductively) by: n n The empty string is balanced If w is balanced, so is (w) If w, x are balanced, so is wx Nothing else is balanced except by the above rules • Remark: a grammar for balanced strings is: • Examples: n n Balanced Unbalanced C SC 473 Automata, Grammars & Languages 41

Parentheses (cont’d) • Defn (C): A string w over {(, )} has the prefix property C iff • Note: the prefix property can be checked in a L-R scan of the string using a counter (this is what calculators do) • Thm: A string w is balanced iff it has the prefix property. n Comment: this iff ( , a logical equivalence) means we have to prove 2 directions s s If a string is balanced, it has the prefix property ( ) (Lemma 1 below) If a string has the prefix property, then it is balanced ( ) (Lemma 2) C SC 473 Automata, Grammars & Languages 42

Parentheses (cont”d) ( ( ( ) ) ( ( C SC 473 Automata, Grammars & Languages ) ) ( ( ( ) ) 43

Parentheses (cont’d) • Thm: A word w is balanced iff it has the prefix property. • Lemma 1: w balanced w has prefix property C. Pf: Induction on |w| Base: |w|=0 w= w satisfies C. Step: Let |w|=n. Assume (IH) all strings shorter than n that are balanced satisfy C. Let w be balanced. Two cases are possible: Case w=uv where u, v are balanced. By IH, u, v satisfy C. Then and so w satisfies C(a). Next consider a prefix s of w=uv. If s is a prefix of u then because by IH, then w satisfies C(b) for this prefix. C SC 473 Automata, Grammars & Languages 44

Parentheses (cont’d) If s = ut where t is a prefix of v then by IH, and so w satisfies C(b) in this case. Case w=(u) where u is balanced. By IH u satisfies C, and so clearly so does (u) � C SC 473 Automata, Grammars & Languages 45

Parentheses (cont’d) • Lemma 2: w satisfies C w is balanced. Pf: Induction on |w| Base: w= is balanced by definition. Step: Let |w|=n >0. Assume (IH) all strings shorter than n that satisfy C are balanced. Let w have prefix property C. Let x be the shortest prefix of w such that Such a prefix exits since w has this property. Case x=w Then w =(u) where u satisfies C. By IH, u is balanced, and so then so is w. Case xv=w with v . Now x satisfies C(a) by assumption and satisfies C(b) since w does. So by IH x is balanced. C SC 473 Automata, Grammars & Languages 46

Parentheses (cont’d) We claim that v has property C. Since and then and so v satisfies C(a). Suppose there were a prefix y of v such that Then Which would violate the prefix property of w. Thus it must be that So v satisfies C(b). By IH, v is balanced. Since both x and v are balanced, w=xv is balanced. � C SC 473 Automata, Grammars & Languages 47