Apple Pi Robotics Gaining a Mechanical Advantage Mechanics

Apple Pi Robotics Gaining a Mechanical Advantage

Mechanics 101 – Gaining an Advantage Levers Belts/Pulleys – Chain/Sprockets Gears Let's talk Forces!
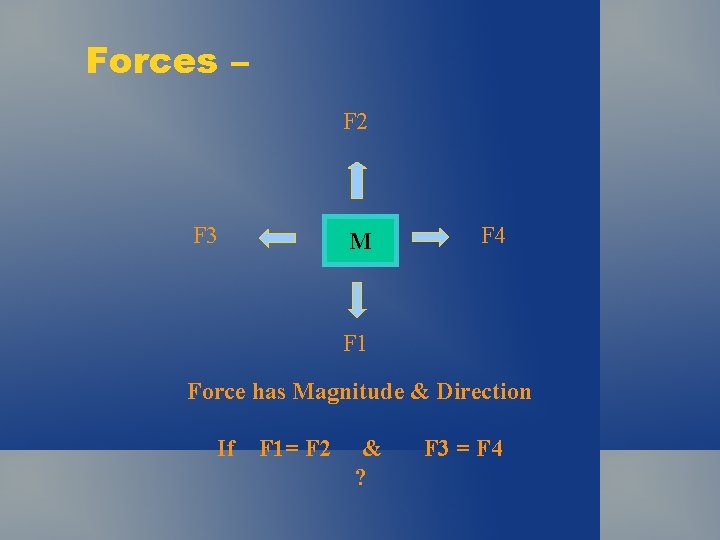
Forces – F 2 F 3 M F 4 F 1 Force has Magnitude & Direction If F 1= F 2 & ? F 3 = F 4
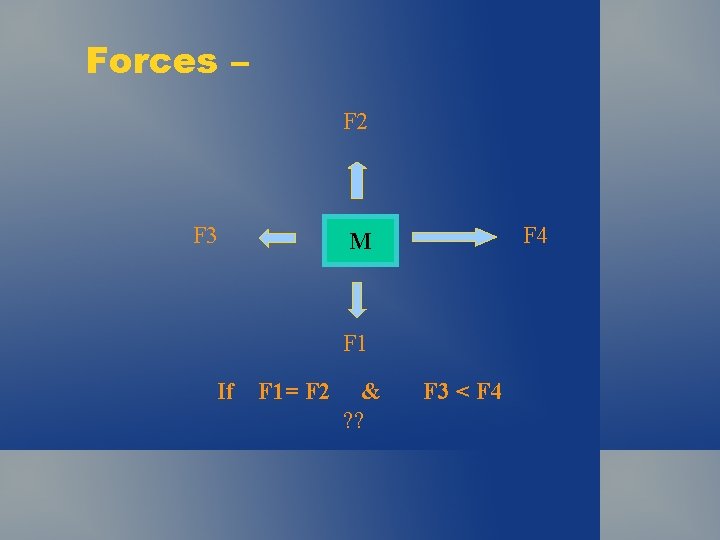
Forces – F 2 F 3 F 4 M F 1 If F 1= F 2 & ? ? F 3 < F 4
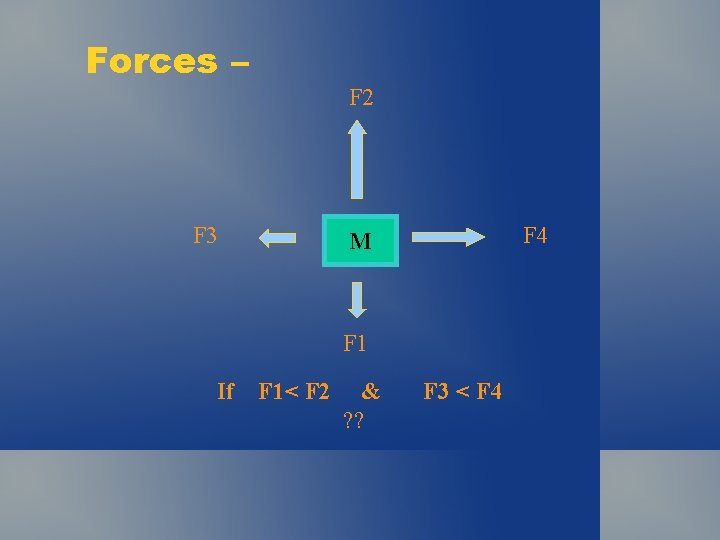
Forces – F 2 F 3 F 4 M F 1 If F 1< F 2 & ? ? F 3 < F 4
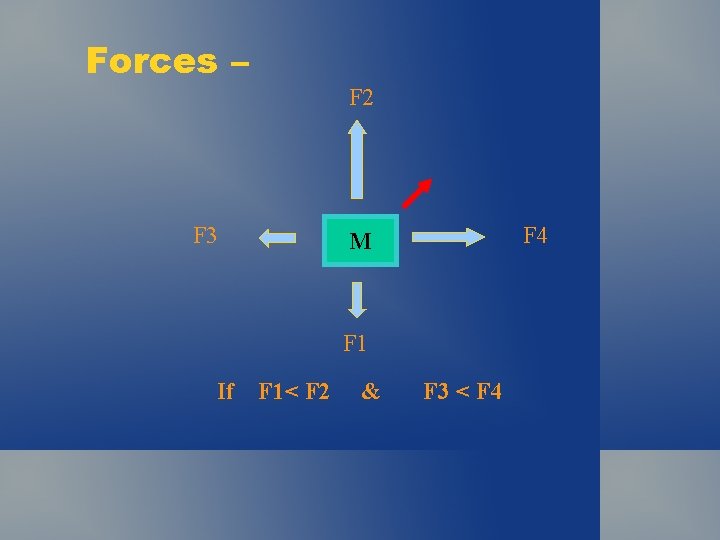
Forces – F 2 F 3 F 4 M F 1 If F 1< F 2 & F 3 < F 4

Practical Example: Static Model F/2 F = mass x a (gravity) = Weight

Practical Example: Dynamic Model F 1 is all about Torque at Wheels (HP is the product of speed and torque) wt f 2 is friction due to windage F 2 is reaction force (tire friction) F 1 F 2 (F 1 -f 2) = mass x acceleration or (F 1 -f 2)/mass = acceleration Provided there is enough reaction force (F 2) to support F 1 F 2 = u * wt/2 (approx)

Practical Example: Windage is proportional to speed 2 uw. V 2 ma = uw. V 2 We have reached terminal velocity F=ma (mass of body x gravitational acceleration)

Types of Forces F(external)= mass * acceleration F(friction)=u * Wt F(weight) = Wt = mass* acceleration(gravity) F(wind)= windage const. * velocity 2 F(impulse) = mass * velocity change

Coefficients of Friction (examples) Materials Aluminum Copper Brass Cast Iron Concrete (wet) Concrete (dry) Polyethylene Steel Copper Rubber Steel Coefficient. 61. 53. 51 1. 05. 30 1. 0. 20
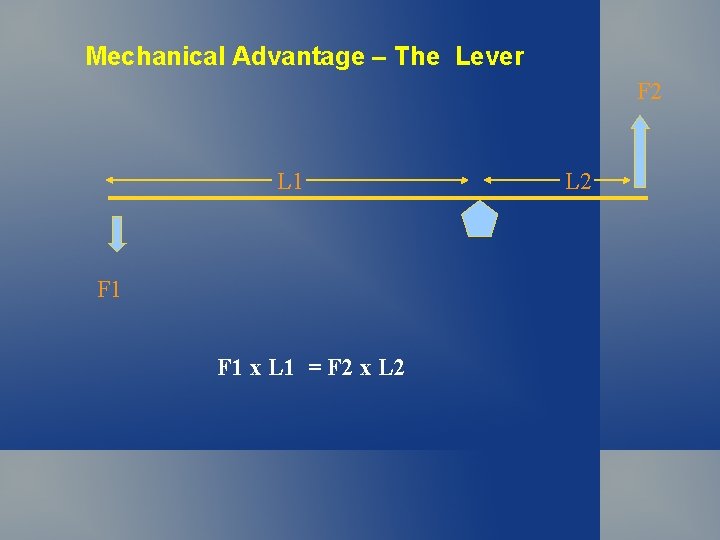
Mechanical Advantage – The Lever F 2 L 1 F 1 x L 1 = F 2 x L 2
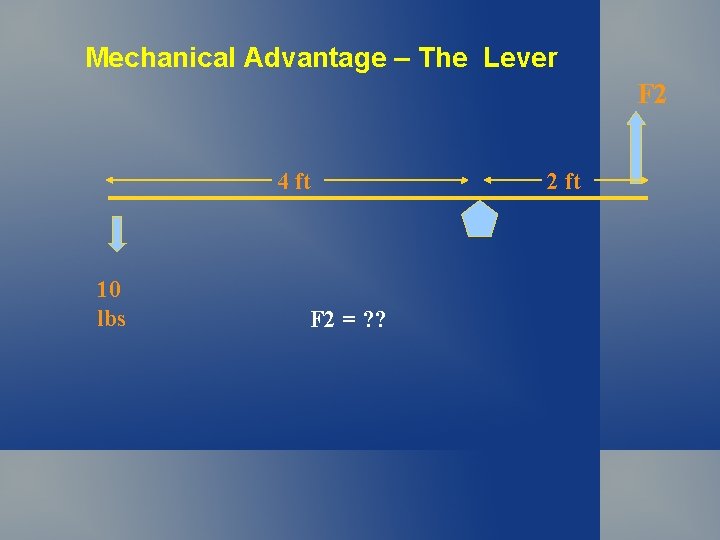
Mechanical Advantage – The Lever F 2 4 ft 10 lbs F 2 = ? ? 2 ft
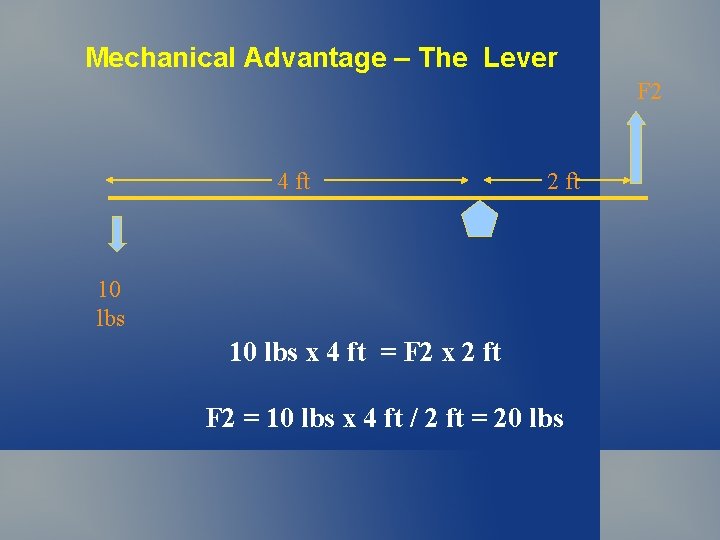
Mechanical Advantage – The Lever F 2 4 ft 2 ft 10 lbs x 4 ft = F 2 x 2 ft F 2 = 10 lbs x 4 ft / 2 ft = 20 lbs
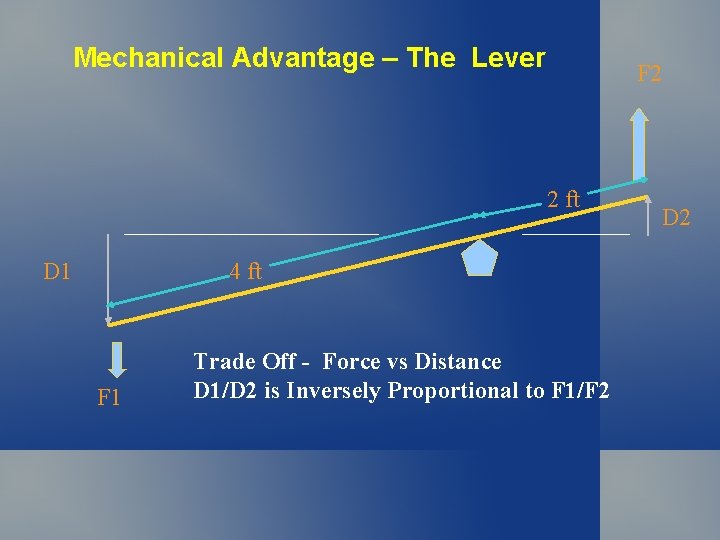
Mechanical Advantage – The Lever F 2 2 ft D 1 4 ft F 1 Trade Off - Force vs Distance D 1/D 2 is Inversely Proportional to F 1/F 2 D 2
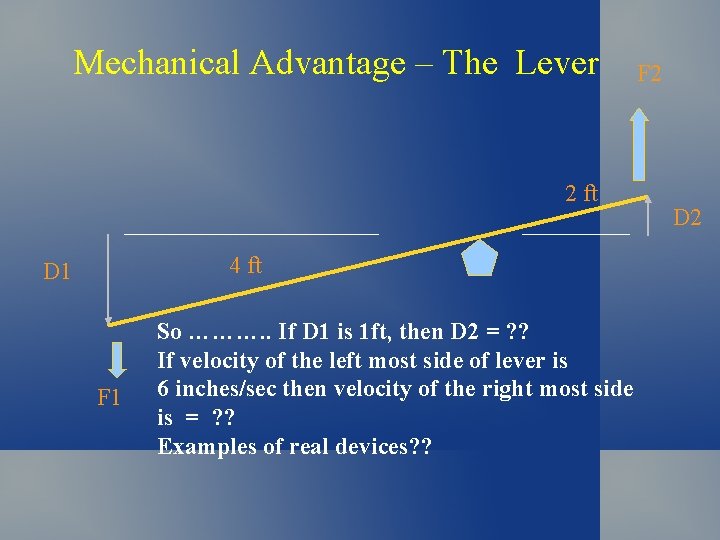
Mechanical Advantage – The Lever 2 ft 4 ft D 1 F 1 So ………. . If D 1 is 1 ft, then D 2 = ? ? If velocity of the left most side of lever is 6 inches/sec then velocity of the right most side is = ? ? Examples of real devices? ? F 2 D 2
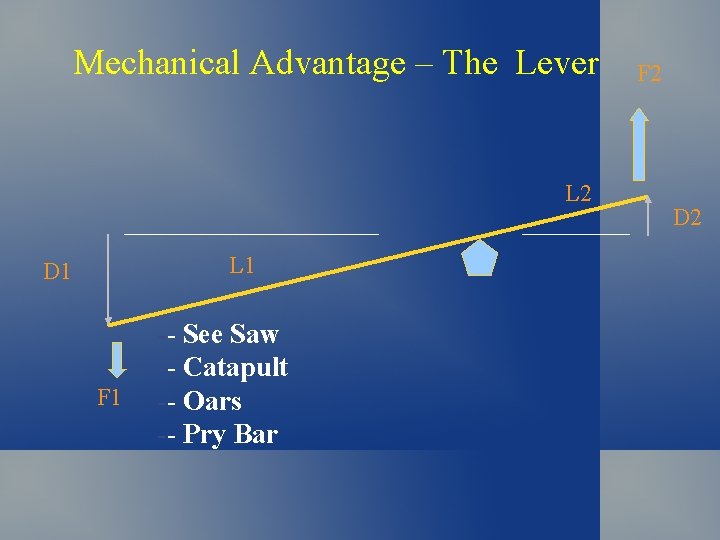
Mechanical Advantage – The Lever L 2 L 1 D 1 F 1 -- See Saw -- Catapult -- Oars -- Pry Bar F 2 D 2
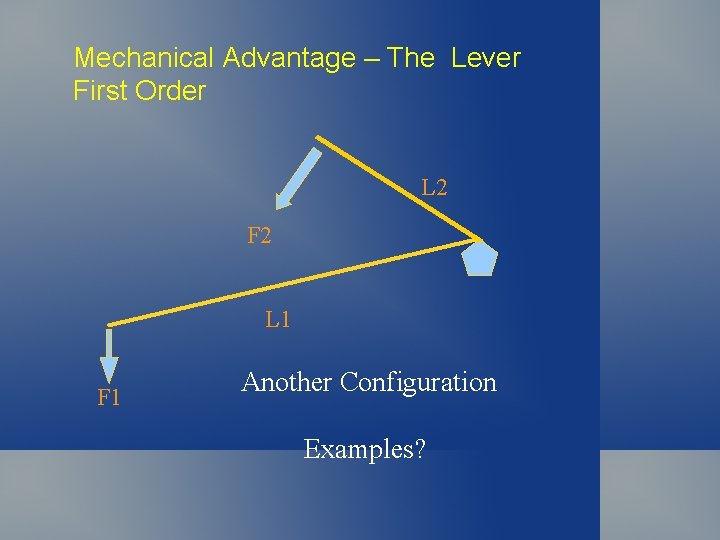
Mechanical Advantage – The Lever First Order L 2 F 2 L 1 F 1 Another Configuration Examples?
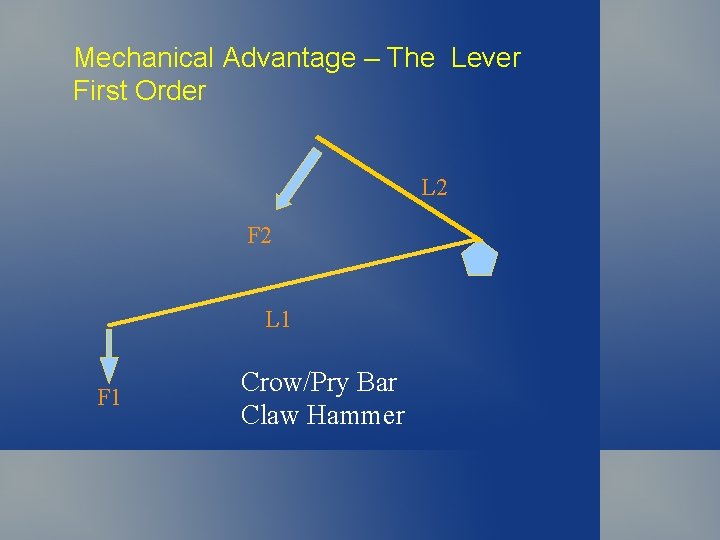
Mechanical Advantage – The Lever First Order L 2 F 2 L 1 F 1 Crow/Pry Bar Claw Hammer
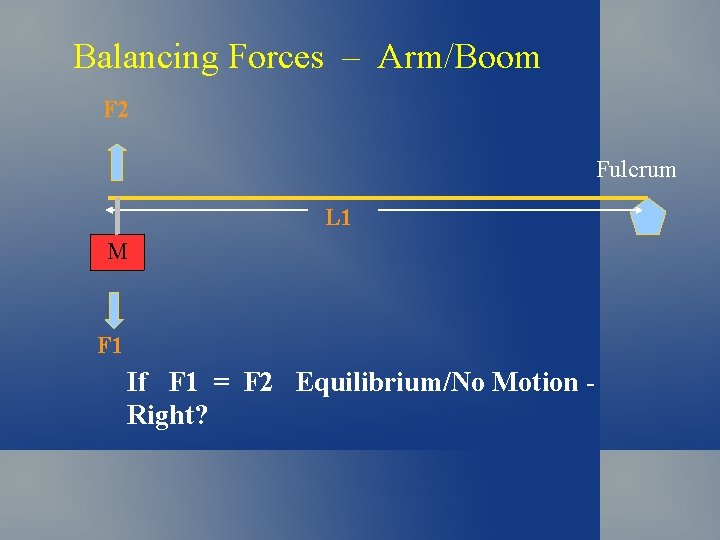
Balancing Forces – Arm/Boom F 2 Fulcrum L 1 M F 1 If F 1 = F 2 Equilibrium/No Motion Right?
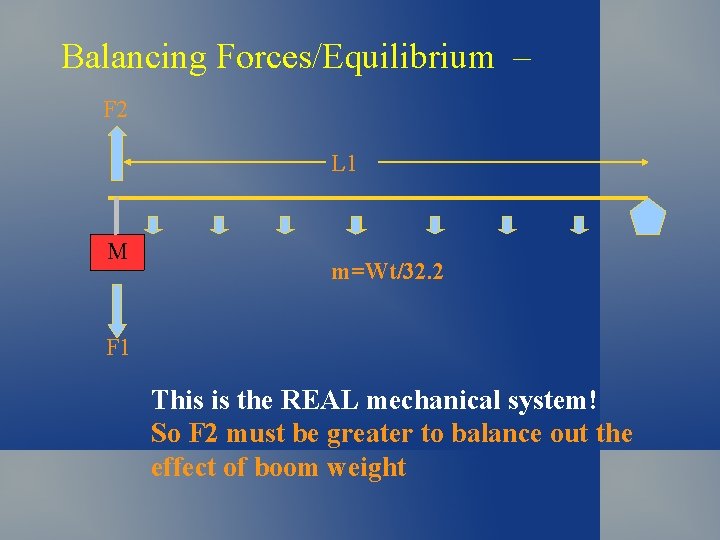
Balancing Forces/Equilibrium – F 2 L 1 M m=Wt/32. 2 F 1 This is the REAL mechanical system! So F 2 must be greater to balance out the effect of boom weight
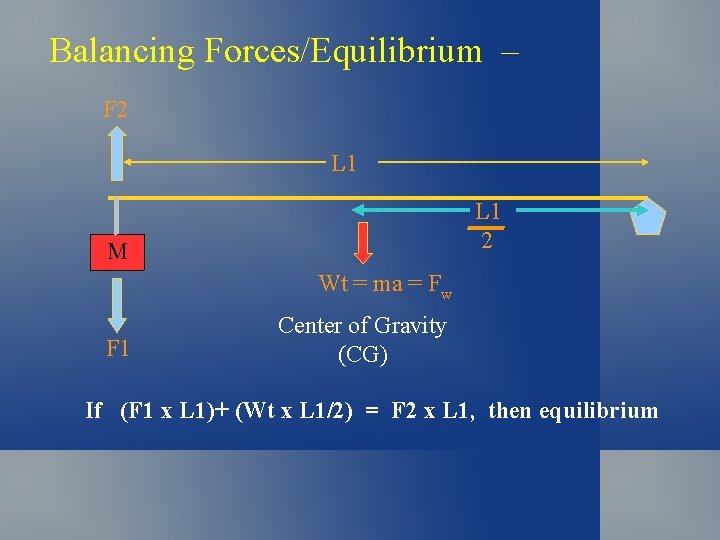
Balancing Forces/Equilibrium – F 2 L 1 2 M Wt = ma = Fw F 1 Center of Gravity (CG) If (F 1 x L 1)+ (Wt x L 1/2) = F 2 x L 1, then equilibrium
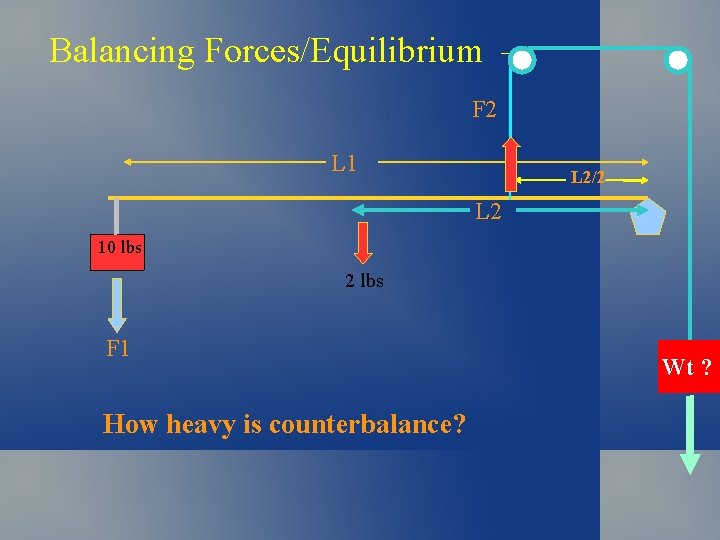
Balancing Forces/Equilibrium – F 2 L 1 L 2/2 L 2 10 lbs 2 lbs F 1 How heavy is counterbalance? Wt ?
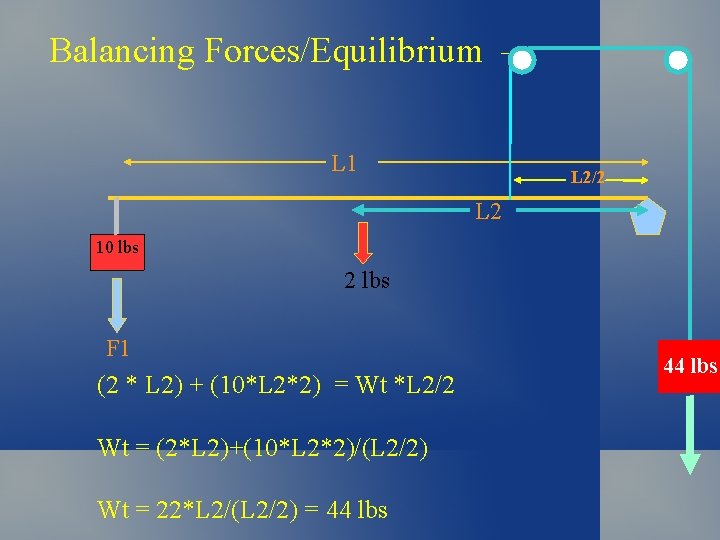
Balancing Forces/Equilibrium – L 1 L 2/2 L 2 10 lbs 2 lbs F 1 (2 * L 2) + (10*L 2*2) = Wt *L 2/2 Wt = (2*L 2)+(10*L 2*2)/(L 2/2) Wt = 22*L 2/(L 2/2) = 44 lbs
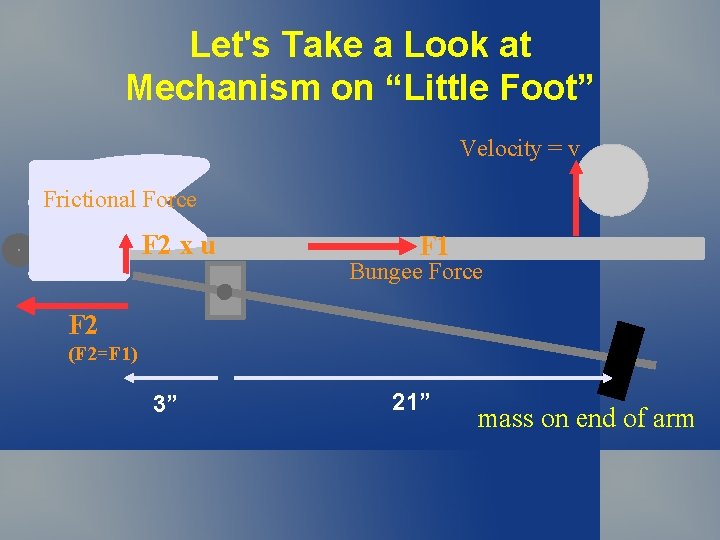
Let's Take a Look at Mechanism on “Little Foot” Velocity = v Frictional Force F 2 x u F 1 Bungee Force F 2 (F 2=F 1) 3” 21” mass on end of arm
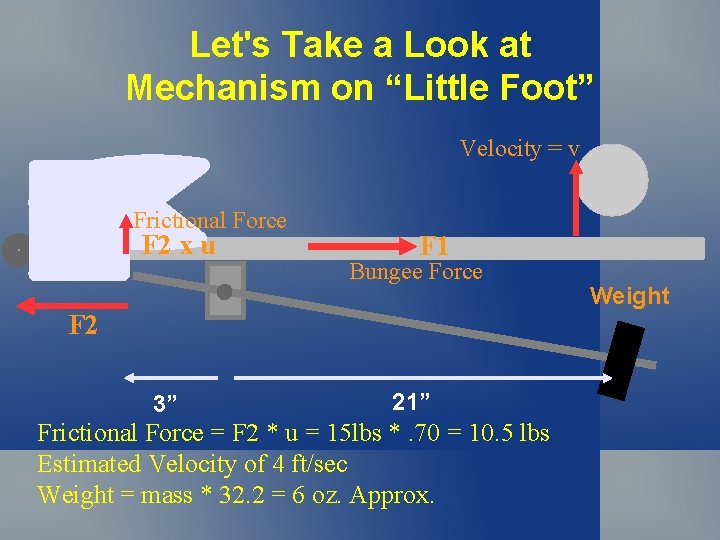
Let's Take a Look at Mechanism on “Little Foot” Velocity = v Frictional Force F 2 x u F 1 Bungee Force F 2 3” 21” Frictional Force = F 2 * u = 15 lbs *. 70 = 10. 5 lbs Estimated Velocity of 4 ft/sec Weight = mass * 32. 2 = 6 oz. Approx. Weight

Inertial Switch Mechanism on “Little Foot” Gain lever advantage of 7: 1 (21” / 3”) Assume 4 ft/sec velocity at end of arm We have accelerated a 6 oz. weight and will be decelerating “very quickly” (. 02 secs? ) m = 1/3 lb / 32. 2 ft/sec 2 Kinetic energy stored = mv Pulse Energy = m (v 1 -v 2) = F(t 1 -t 2) – For our example this calculates to approx. lbs force 15 Approx. 50% greater than our calculated frictional
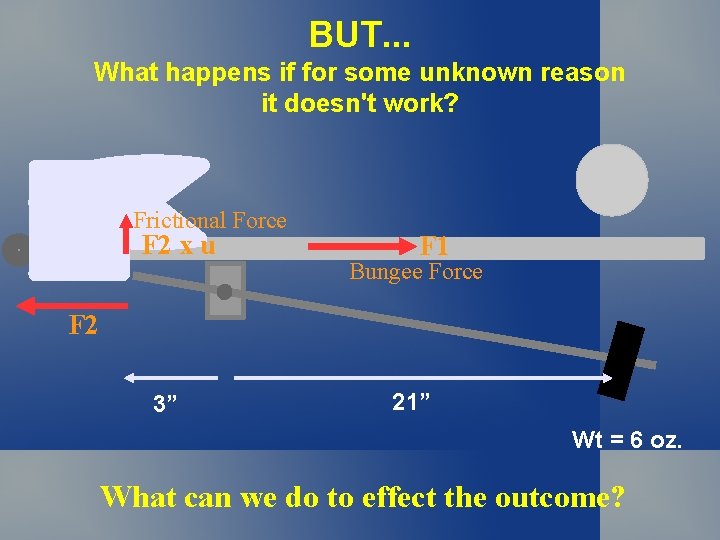
BUT. . . What happens if for some unknown reason it doesn't work? Frictional Force F 2 x u F 1 Bungee Force F 2 3” 21” Wt = 6 oz. What can we do to effect the outcome?
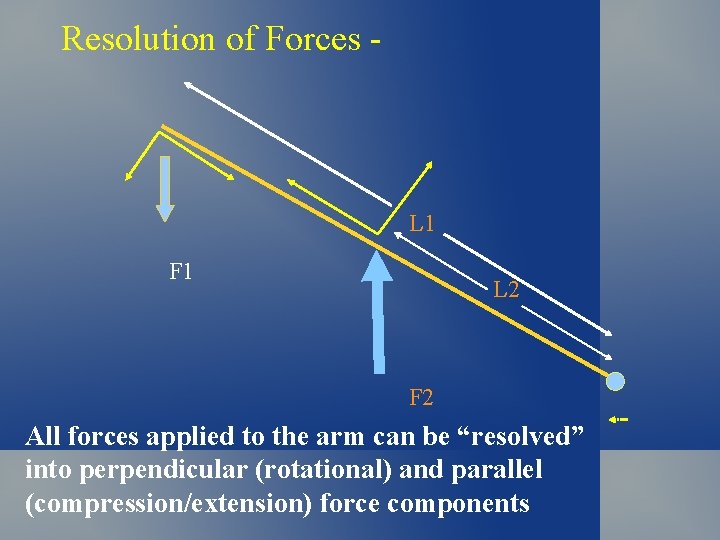
Resolution of Forces - L 1 F 1 L 2 F 2 All forces applied to the arm can be “resolved” into perpendicular (rotational) and parallel (compression/extension) force components
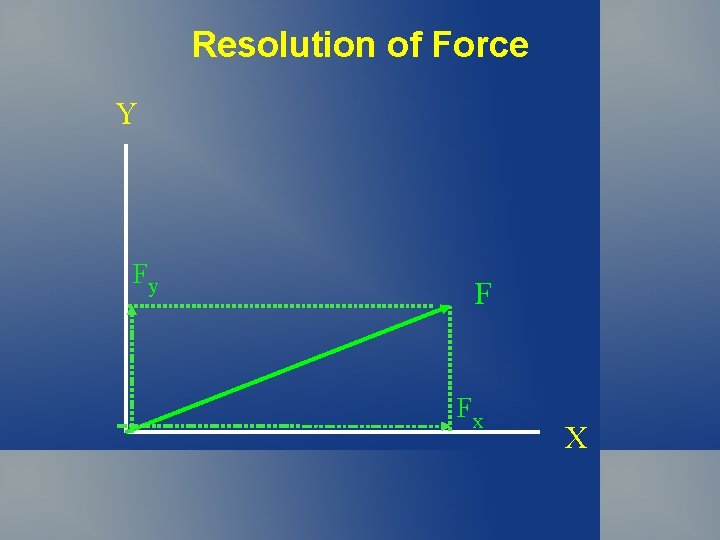
Resolution of Force Y Fy F Fx X

Resolution of Force How? A Little Math F Fy O Fx Using SIN, COS & TAN Functions If any two are known you can solve for any others
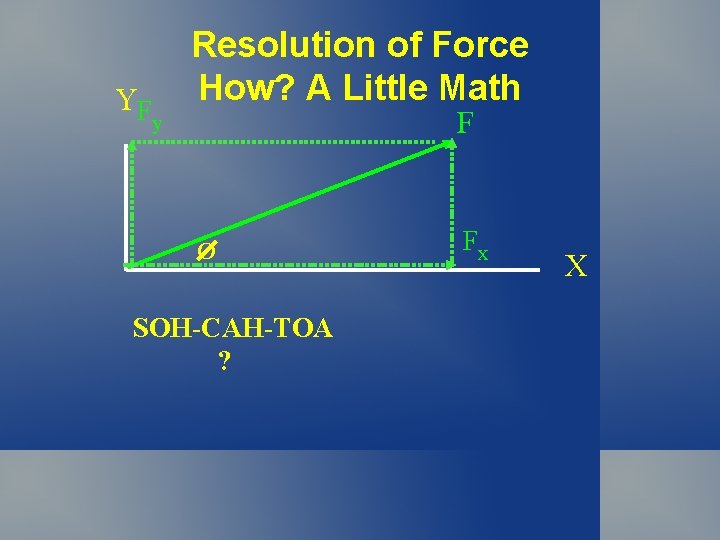
YF Resolution of Force How? A Little Math F y O SOH-CAH-TOA ? Fx X
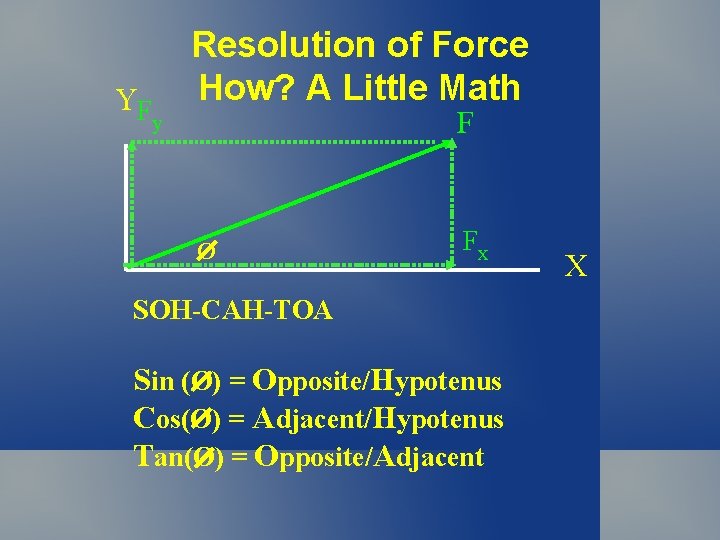
YF Resolution of Force How? A Little Math F y O Fx SOH-CAH-TOA Sin (O) = Opposite/Hypotenus Cos(O) = Adjacent/Hypotenus Tan(O) = Opposite/Adjacent X
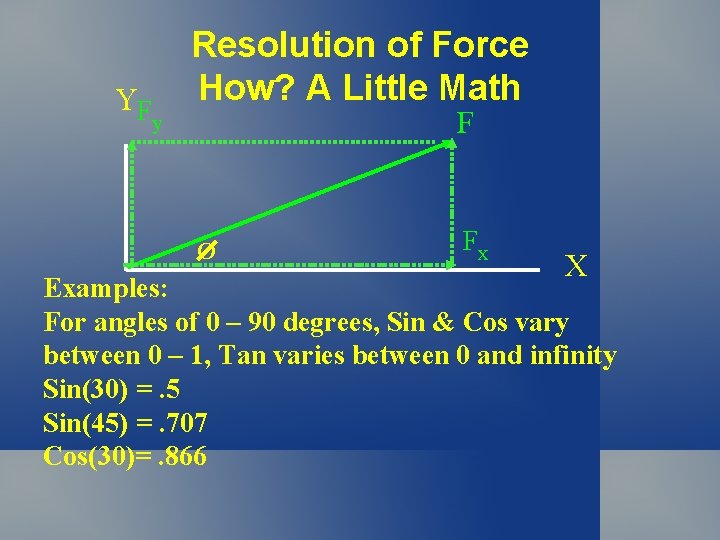
YF Resolution of Force How? A Little Math F y O Fx X Examples: For angles of 0 – 90 degrees, Sin & Cos vary between 0 – 1, Tan varies between 0 and infinity Sin(30) =. 5 Sin(45) =. 707 Cos(30)=. 866
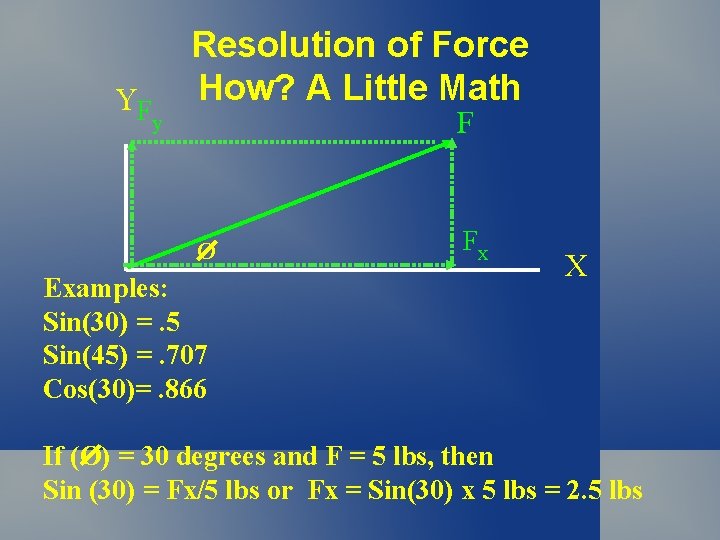
YF Resolution of Force How? A Little Math F y O Examples: Sin(30) =. 5 Sin(45) =. 707 Cos(30)=. 866 Fx X If (O) = 30 degrees and F = 5 lbs, then Sin (30) = Fx/5 lbs or Fx = Sin(30) x 5 lbs = 2. 5 lbs
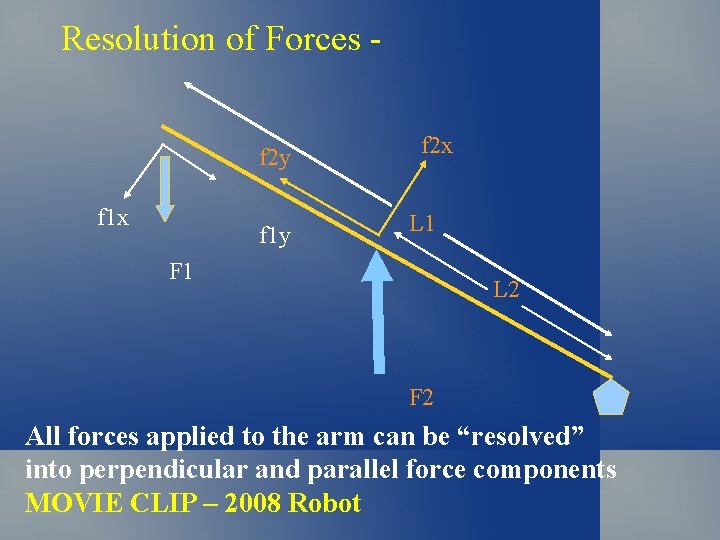
Resolution of Forces f 2 y f 1 x f 1 y f 2 x L 1 F 1 L 2 F 2 All forces applied to the arm can be “resolved” into perpendicular and parallel force components MOVIE CLIP – 2008 Robot
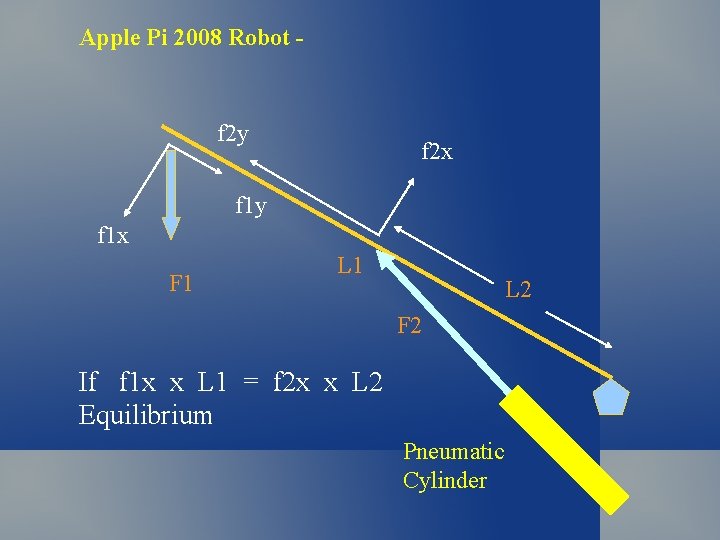
Apple Pi 2008 Robot - f 2 y f 2 x f 1 y f 1 x F 1 L 2 F 2 If f 1 x x L 1 = f 2 x x L 2 Equilibrium Pneumatic Cylinder

Belts-Sheaves and Chain-Sprockets

Belts, Sheaves & Sprockets Belt Types V - belt Flat belt Does slip Depends on tension Cogged generally solidly “coupled” to sprocket Teeth molded into belt Mesh with slots in pulley Flat or V groove No slip/highly efficient

Pulleys/Sprockets Configuration of pulleys with belt to gain mechanical advantage Dia. = 1” P#1 Each pulley has a circumference of (Pi) x D So pulley 1 has a circumference of 3. 14” while pulley 2 has a circumference of 12. 56”. It will take 4 revolutions of P 1 to “feed out” enough belt to allow for 12. 56” of the circumference of P 2 to be “conveyed”. (assuming no slippage) P#2 Pulley #2 will go at ¼ the speed (RPM's) as P #1 and generate 4 x's the torque Dia. = 4”
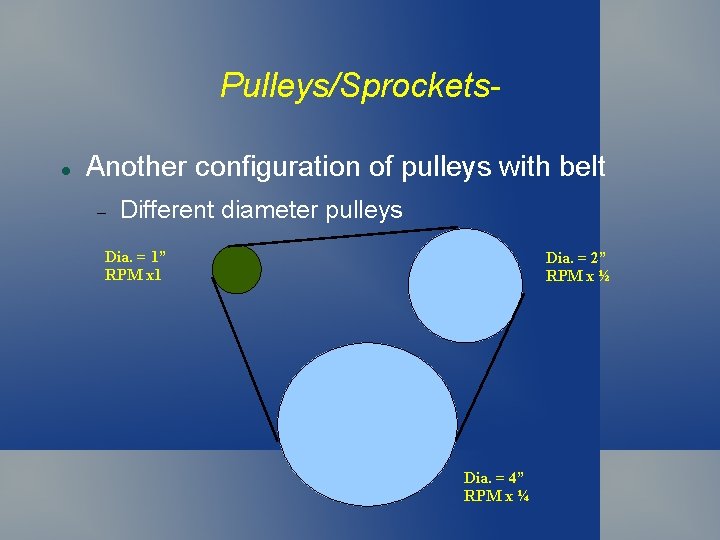
Pulleys/Sprockets Another configuration of pulleys with belt Different diameter pulleys Dia. = 1” RPM x 1 Dia. = 2” RPM x ½ Dia. = 4” RPM x ¼
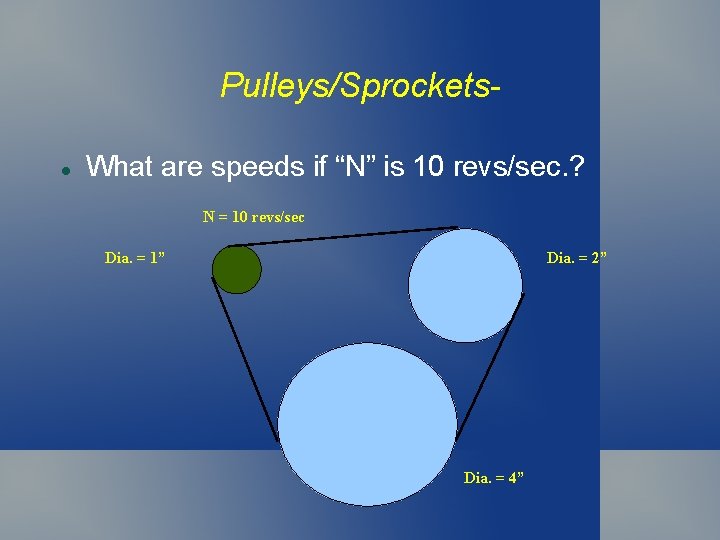
Pulleys/Sprockets What are speeds if “N” is 10 revs/sec. ? N = 10 revs/sec Dia. = 2” Dia. = 1” Dia. = 4”

Belts/Pulley vs. Chain/Sprocket Whats the Difference? * Belts generally used for lower torque requirements * Belts can slip (could be good? ) * Chain can be separated (maintenance) * Belts do not need lubrication

Gears behave like “closely coupled” pulleys Differences – G#2 turns opposite direction & no chance for slippage Each gear has a circumference of (Pi) x D So gear #1 has a circumference of 3. 14” while gear #2 has a circumference of 12. 56”. It will take 4 revolutions of G 1 to “circum navigate” the perimeter of G 2 to allow for 12. 56” of the circumference of G 2 (assuming no slippage) Dia. = 1” G#1 Gear #2 will go at ¼ the speed (RPM's) as Gear #1 G#2 Dia. = 4”

Compound Gears. Previous example showed that G#2 will go at ¼ the speed of G#1. G#3 coupled directly to G#2 so it goes at ¼ the speed also. Then G#4 will go at 1/3 the speed of G#3 since is has 3 times the circumference (or diameter). Total mechanical advantage is 4 x 3 or 12. If G#1 is going 120 RPM's, then G#4 is ? G#1 G#4 = Dia. 3” G#2 G#1 & 3 Dia. = 1” G#4 G#3 G#2 Dia. 4” This compound gear set provides 12: 1 ratio (1/12 the speed) with 12 x's the torque.

“MANTIS” Drive Train Design Speed to be 12 fps CIM Motors have 5000 rpm top speed Will use 2 speed transmission – – High range has 9. 4: 1 gear ratio Chain sprockets available are 12, 15, 22, 26, and 30 tooth Drive wheel is 8” diameter Select drive components after transmission

“MANTIS” Drive Train For 12 fps Wheel circumference of 8” x 3. 14 = 25” (approx) 25 in/rev/12 in/ft = 2. 08 ft/rev X revs/sec = 12 ft/sec/2. 08 ft/rev = 5. 77 revs/sec 5000 rpm = 83 rev/sec (5000 rev/min/60 secs/min) Total ratio is 83 rev/sec/5. 77 rev/sec = 14. 38: 1 Ratio of transmission is 9. 4: 1 so we need additional 14. 38/9. 4 (1. 53: 1) ratio Looking at available sprockets (12, 15, 22, 24 and 30) we picked 22 and 15 (1. 46: 1 ratio)

That's All Folks!
- Slides: 48