APLICACIONES DE LAS DERIVADAS U D 6 2

APLICACIONES DE LAS DERIVADAS U. D. 6 * 2º BCT @ Angel Prieto Benito Apuntes 2º Bachillerato C. T. 1

GRÁFICAS RACIONALES U. D. 6. 5 * 2º BCT @ Angel Prieto Benito Apuntes 2º Bachillerato C. T. 2

A tener en cuenta • Puntos importantes a tener en cuenta para representar funciones RACIONALES, y = P(x) / Q(x) • • • 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. - Asíntotas verticales. Asíntotas horizontales. Asíntotas oblicuas. Máximos y mínimos relativos. Cortes con los ejes. Intervalos de crecimiento y decrecimiento. Puntos de inflexión. Intervalos de concavidad y convexidad. Simetría. Periodicidad. Tabla de Valores. @ Angel Prieto Benito Apuntes 2º Bachillerato C. T. 3

Ejemplo_1 • Representar la función @ Angel Prieto Benito y = x / (3 – x) Apuntes 2º Bachillerato C. T. 4

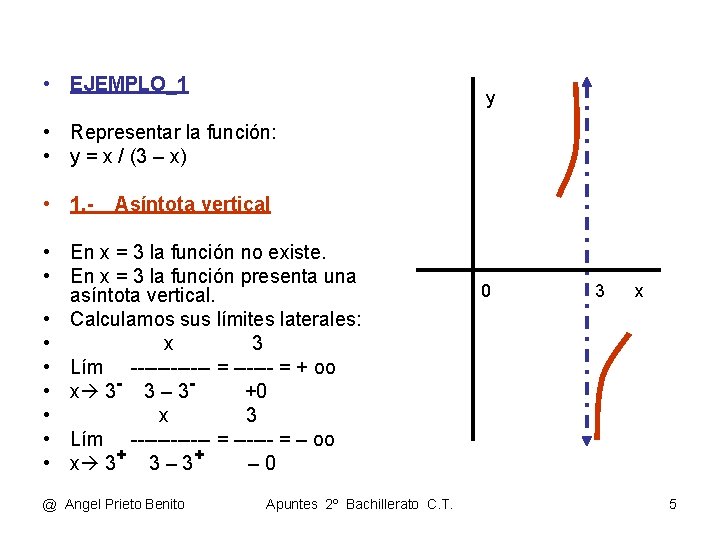
• EJEMPLO_1 y • Representar la función: • y = x / (3 – x) • 1. - Asíntota vertical • En x = 3 la función no existe. • En x = 3 la función presenta una asíntota vertical. • Calculamos sus límites laterales: • x 3 • Lím ------ = + oo • x 3 - 3 – 3+0 • x 3 • Lím ------ = – oo • x 3+ 3 – 3+ – 0 @ Angel Prieto Benito Apuntes 2º Bachillerato C. T. 0 3 x 5

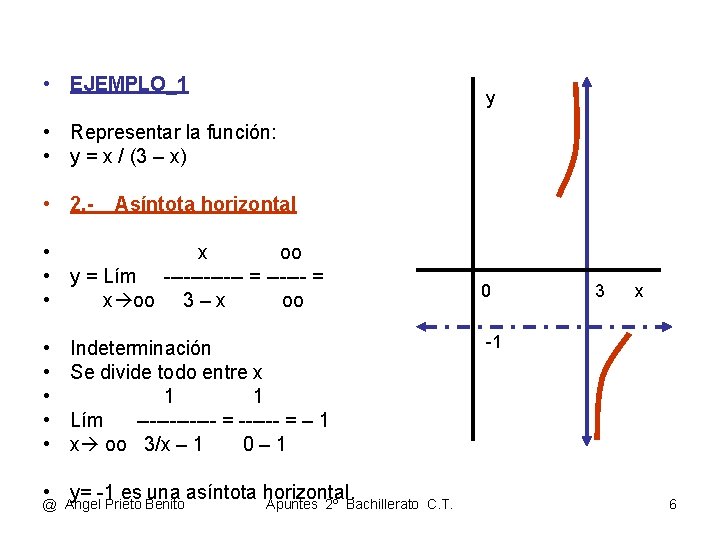
• EJEMPLO_1 y • Representar la función: • y = x / (3 – x) • 2. - Asíntota horizontal • x oo • y = Lím ------ = • x oo 3 – x oo • • • Indeterminación Se divide todo entre x 1 1 Lím ------ = – 1 x oo 3/x – 1 0– 1 • y= -1 es una asíntota horizontal. @ Angel Prieto Benito Apuntes 2º Bachillerato C. T. 0 3 x -1 6

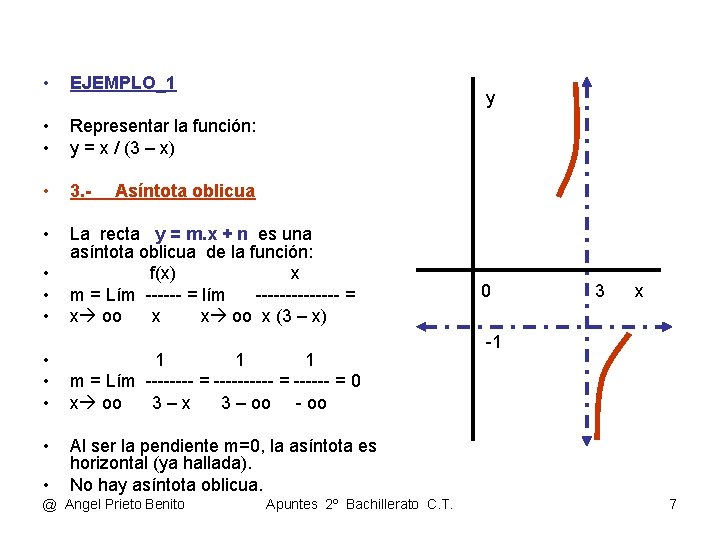
• EJEMPLO_1 • • Representar la función: y = x / (3 – x) • 3. - • La recta y = m. x + n es una asíntota oblicua de la función: f(x) x m = Lím ------ = lím ------- = x oo x (3 – x) • • • y Asíntota oblicua • • • 1 1 1 m = Lím -------- = 0 x oo 3–x 3 – oo - oo • Al ser la pendiente m=0, la asíntota es horizontal (ya hallada). No hay asíntota oblicua. • @ Angel Prieto Benito Apuntes 2º Bachillerato C. T. 0 3 x -1 7

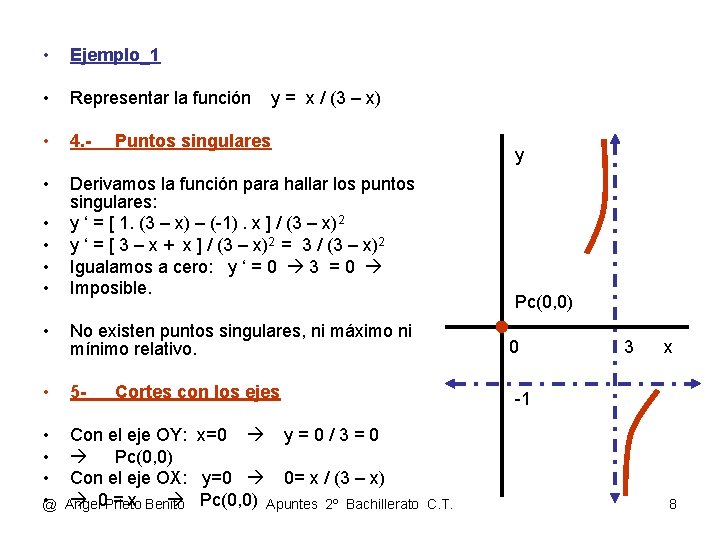
• Ejemplo_1 • Representar la función • 4. - • Derivamos la función para hallar los puntos singulares: y ‘ = [ 1. (3 – x) – (-1). x ] / (3 – x)2 y ‘ = [ 3 – x + x ] / (3 – x)2 = 3 / (3 – x)2 Igualamos a cero: y ‘ = 0 3 = 0 Imposible. • • y = x / (3 – x) Puntos singulares • No existen puntos singulares, ni máximo ni mínimo relativo. • 5 - • • @ Con el eje OY: x=0 y = 0 / 3 = 0 Pc(0, 0) Con el eje OX: y=0 0= x / (3 – x) 0 Prieto = x Benito Pc(0, 0) Apuntes 2º Bachillerato Angel y Pc(0, 0) 0 Cortes con los ejes 3 x -1 C. T. 8

• Ejemplo 1: • Representar la función • 6. - y = x / (3 – x) Intervalos de crecimiento y decrecimiento: • Su derivada era y ‘ = 3 / ( 3 – x)2 • Al no haber puntos singulares, x = 3, que es la asíntota vertical, nos delimita los intervalos • Los intervalos a estudiar son: (-oo, 3) y (3, oo) • Tomamos un punto cualquiera de cada intervalo: • f ’ (0) = 3 / (3 – 0)2 = 3 / 9 = 1 / 3 > 0 Creciente en (- oo, 3) • f ’ ( 6) = 3 / (3 – 6)2 = 3 / 9 = 1/ 3 > 0 Creciente en (3, + oo) @ Angel Prieto Benito Apuntes 2º Bachillerato C. T. 9

• Ejemplo 1: • Representar la función • 7. • • y = x / (3 – x) Puntos de Inflexión: Su derivada era y ‘ = 3 / (3 – x)2 Hallamos la segunda derivada: y ’’ = [ 0. (3 – x)2 – 3. 2. (3 – x). ( - 1)] / (3 – x)4 y ’’ = [ 6. (3 – x)] / (3 – x)4 = 6 / (3 – x)3 • Igualamos a cero: • 6 / (3 – x)3 = 0 6 = 0 Imposible. No existen puntos de inflexión. • No procede comprobar que y’’’ <> 0 @ Angel Prieto Benito Apuntes 2º Bachillerato C. T. 10

• Ejemplo 1: • Representar la función • 8. - y = x / (3 – x) Intervalos de concavidad y convexidad: • Su derivada era y ‘ = 3 / (3 – x)2 • Su segunda derivada era: y ’’ = 6 / (3 – x)3 • Como no hay Puntos de Inflexión, los límites de los intervalos vendrán dados por la asíntota vertical x = 3 • Los intervalos a estudiar son: (- oo, 3) y (3, + oo) • Tomamos un punto cualquiera de cada intervalo: • f ‘’ (0) = 6 / 33 > 0 Es Cóncava en (- oo, 3) • f ‘’ (6) = 6 / (3 – 6)3 = 6 / (- 33) < 0 Es Convexa en (3, + oo) @ Angel Prieto Benito Apuntes 2º Bachillerato C. T. 11

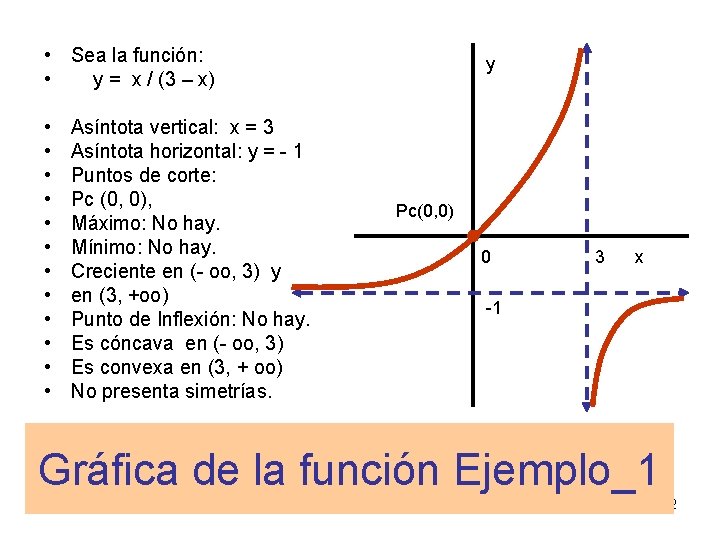
• Sea la función: • y = x / (3 – x) • • • y Asíntota vertical: x = 3 Asíntota horizontal: y = - 1 Puntos de corte: Pc (0, 0), Máximo: No hay. Mínimo: No hay. Creciente en (- oo, 3) y en (3, +oo) Punto de Inflexión: No hay. Es cóncava en (- oo, 3) Es convexa en (3, + oo) No presenta simetrías. Pc(0, 0) 0 3 x -1 Gráfica de la función Ejemplo_1 @ Angel Prieto Benito Apuntes 2º Bachillerato C. T. 12

Ejemplo_2 • Representar la función y = (x 2 + 3) / (4. x – x 2) @ Angel Prieto Benito Apuntes 2º Bachillerato C. T. 13

• EJEMPLO_2 • • Representar la función: y = (x 2 + 3) / (4. x – x 2) • 1. - • En x = 0 y x = 4 la función no existe al dar cero el numerador. x = 0 es una asíntota vertical. x = 4 es una asíntota vertical. Calculamos sus límites laterales: x 2 + 3 3 Lím ------ = - oo x 0 - 4. x – x 2 0 - – 0 x 2 + 3 3 Lím ------ = + oo x 0+ 4. x – x 2 0+ – 0+ • • • y Asíntotas verticales 0 4 x Pues en valores muy próximos a 0, 4 x es mayor que x 2 @ Angel Prieto Benito Apuntes 2º Bachillerato C. T. 14

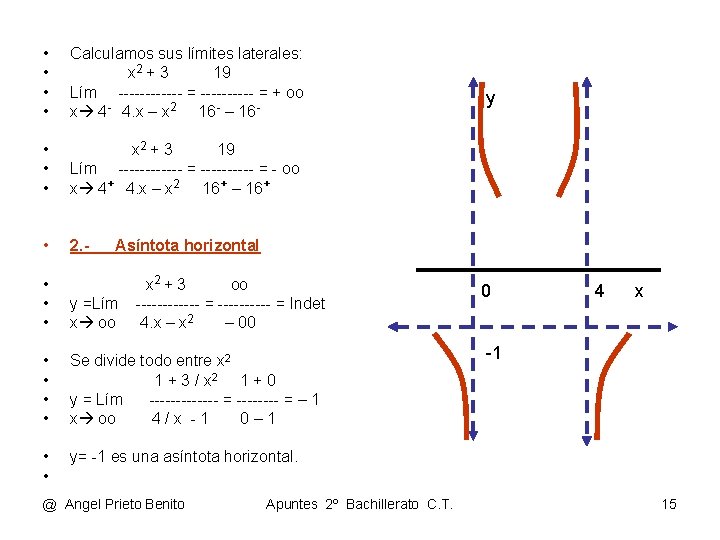
• • Calculamos sus límites laterales: x 2 + 3 19 Lím ------ = + oo x 4 - 4. x – x 2 16 - – 16 - • • • x 2 + 3 19 Lím ------ = - oo x 4+ 4. x – x 2 16+ – 16+ • 2. - y Asíntota horizontal x 2 + 3 oo ------ = Indet 4. x – x 2 – 00 • • • y =Lím x oo • • Se divide todo entre x 2 1 + 3 / x 2 1 + 0 y = Lím ------- = – 1 x oo 4/x -1 0– 1 • • y= -1 es una asíntota horizontal. @ Angel Prieto Benito Apuntes 2º Bachillerato C. T. 0 4 x -1 15

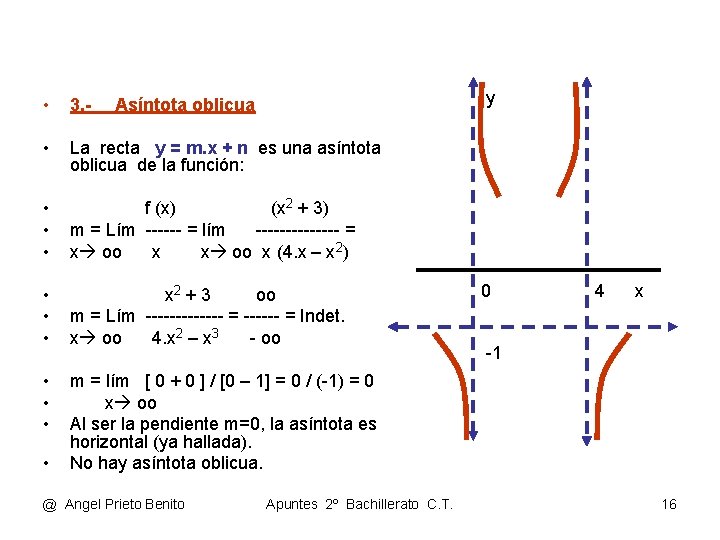
y • 3. - • La recta y = m. x + n es una asíntota oblicua de la función: • • • f (x) (x 2 + 3) m = Lím ------ = lím ------- = x oo x (4. x – x 2) • • • x 2 + 3 oo m = Lím ------- = Indet. x oo 4. x 2 – x 3 - oo • • • m = lím [ 0 + 0 ] / [0 – 1] = 0 / (-1) = 0 x oo Al ser la pendiente m=0, la asíntota es horizontal (ya hallada). No hay asíntota oblicua. • Asíntota oblicua @ Angel Prieto Benito Apuntes 2º Bachillerato C. T. 0 4 x -1 16

• 4. - • y = (x 2 + 3) / (4. x – x 2) • • Derivamos la función para hallar los puntos singulares: y ‘ = [ 2 x. (4. x – x 2) – (x 2 + 3 ). (4 – 2. x ] / (4. x – x 2)2 y ‘ = [ 8. x 2 – 2. x 3 – 4. x 2 + 2. x 3 – 6. x – 12 ] / (4. x – x 2)2 y ‘ = ( 4. x 2 – 6. x – 12 ) / (4. x – x 2)2 • • Igualamos a cero: y ‘ = 0 4. x 2 – 6. x – 12 = 0 2. x 2 – 3. x – 6 = 0 Resolvemos la ecuación: x = [ 3 +/- √ (9 + 48) ] / 4 = (3 +/- 7, 55) / 4 x = 2, 64 y x = - 1, 16 son las abscisas de los puntos singulares. • Calculamos sus ordenadas: • • f(2, 64) = (2, 642 + 3) / (4. 2, 64 – 2, 642) = 9, 97 / 3, 59 = 2, 77 f(-1, 16) = ((-1, 16)2 + 3) / (4. (-1, 16) – (-1, 16)2) = 4, 34 / (-5, 98) = -0, 72 • Los puntos son: (-1, 16, -0, 72) y (2, 64, 2, 77) • Puntos singulares @ Angel Prieto Benito Apuntes 2º Bachillerato C. T. 17

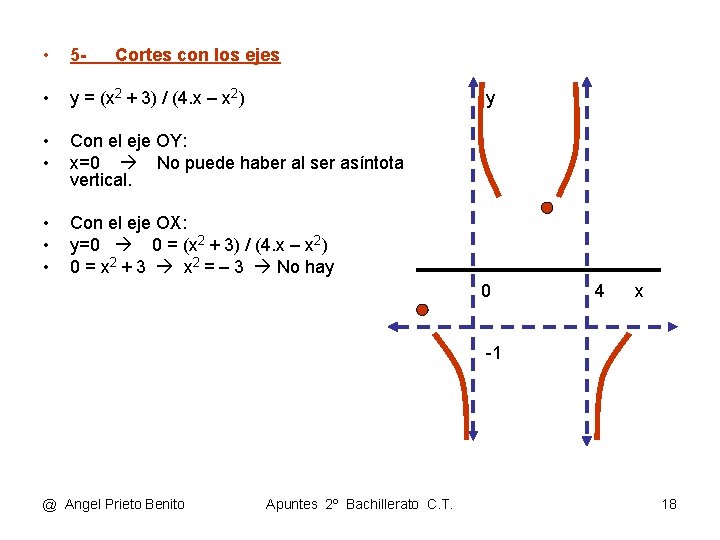
• 5 - • y = (x 2 + 3) / (4. x – x 2) • • Con el eje OY: x=0 No puede haber al ser asíntota vertical. • • • Con el eje OX: y=0 0 = (x 2 + 3) / (4. x – x 2) 0 = x 2 + 3 x 2 = – 3 No hay Cortes con los ejes y 0 4 x -1 @ Angel Prieto Benito Apuntes 2º Bachillerato C. T. 18

• 6. - • • • y = (x 2 + 3) / (4. x – x 2) Su derivada era: y ‘ = ( 4. x 2 – 6. x – 12 ) / (4. x – x 2)2 • • • Los puntos singulares y las asíntotas verticales nos delimita los intervalos Los intervalos a estudiar son: (- oo, -1, 16) , (-1, 16, 0) , (0, 2, 64) , (2, 64, 4) y (4, + oo) • • • @ Tomamos un punto cualquiera de cada intervalo: f ’ (-2) = ( 4. (-2)2 – 6. (-2) – 12 ) / (4. (-2) – (-2)2)2 = 16/144 > 0 Creciente en (- oo, -1, 16) f ’ (-1) = ( 4. (-1)2 – 6. (-1) – 12 ) / (4. (-1) – (-1)2)2 = -2 / 25 <0 Decreciente en (-1, 16, 0) f ’ (2) = ( 4. 22 – 6. 2 – 12 ) / (4. 2 – 22)2 = - 8 /16 < 0 Decreciente en (0, 2, 64) f ’ (3) = ( 4. 32 – 6. 3 – 12 ) / (4. 3 – 32)2 = 6 / 9 > 0 Creciente en (2, 64, + oo) f ’ (5) = ( 4. 52 – 6. 5 – 12 ) / (4. 5 – 52)2 = 58 / 25 > 0 Creciente en (2, 64, + oo) Angel Prieto Benito Apuntes 2º Bachillerato C. T. Intervalos de crecimiento y decrecimiento: 19

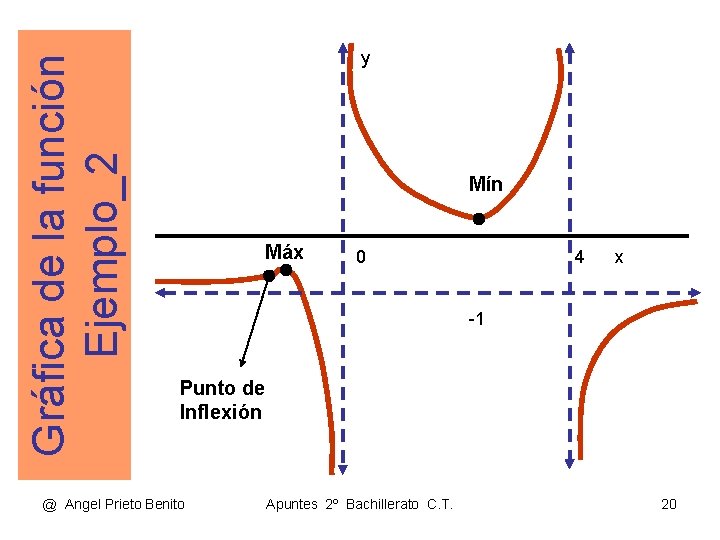
Gráfica de la función Ejemplo_2 y Mín Máx 0 4 x -1 Punto de Inflexión @ Angel Prieto Benito Apuntes 2º Bachillerato C. T. 20