APLICACIONES DE LAS DERIVADAS U D 6 2

APLICACIONES DE LAS DERIVADAS U. D. 6 * 2º BCT @ Angel Prieto Benito Apuntes 2º Bachillerato C. T. 1

ELEMENTOS GRÁFICOS U. D. 6. 1 * 2º BCT @ Angel Prieto Benito Apuntes 2º Bachillerato C. T. 2

DOMINIO Y RECORRIDO • DOMINIO de f(x): • • Todos los valores de x para los que existe la función. Se denota por Dom f(x) =. . . En las funciones polinómicas el dominio es R. En las funciones racionales el dominio es R – [a, b, c, . . . ], siendo a, b, c, . . los puntos de asíntotas verticales. • • RECORRIDO de f(x): Todos los valores que puede tomar f(x). Se denota por Img f(x) =. . . En las funciones lineales el recorrido es R. En las funciones cuadráticas el recorrido es (-oo, yv] ó (yv , oo), según sea convexa o cóncava. En las funciones cúbicas el recorrido es R. @ Angel Prieto Benito Apuntes 2º Bachillerato C. T. 3

CORTES CON LOS EJES • Corte con el eje OY: • x=0 y = f (0) Pc ( 0, f(0) ) • Corte con el eje OX: • f(x) = 0 xi = Raíces de la función f(x) • • Si una función presenta cortes con el eje OX en los puntos x=a, x=b, x= c, etc , se establecen zonas o regiones donde el signo de la función es el mismo: • (- oo, a) , (a, b) , (b, c) , (c, . . . ) , …, ( k, +oo) • Si una función es positiva / negativa en un punto xo c (a, b) , siendo a y b puntos de corte con el eje OX, la función será positiva / negativa en todos los puntos del intervalo ( a, b ). @ Angel Prieto Benito Apuntes 2º Bachillerato C. T. 4

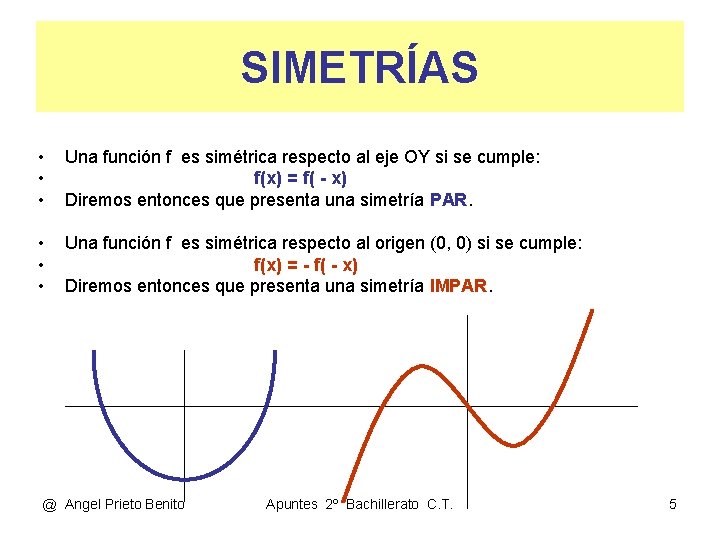
SIMETRÍAS • • • Una función f es simétrica respecto al eje OY si se cumple: f(x) = f( - x) Diremos entonces que presenta una simetría PAR. • • • Una función f es simétrica respecto al origen (0, 0) si se cumple: f(x) = - f( - x) Diremos entonces que presenta una simetría IMPAR. @ Angel Prieto Benito Apuntes 2º Bachillerato C. T. 5

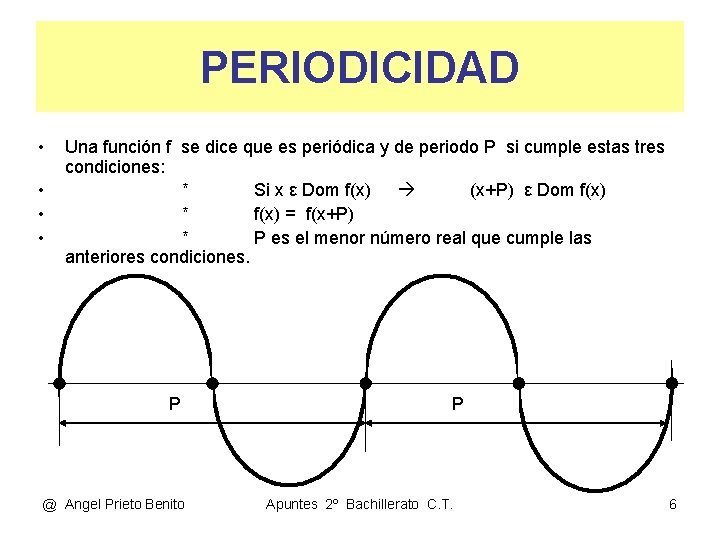
PERIODICIDAD • • Una función f se dice que es periódica y de periodo P si cumple estas tres condiciones: * Si x ε Dom f(x) (x+P) ε Dom f(x) * f(x) = f(x+P) * P es el menor número real que cumple las anteriores condiciones. P @ Angel Prieto Benito P Apuntes 2º Bachillerato C. T. 6

MONOTONÍA • Una función f es CRECIENTE en el intervalo (a, b) si para todos los pares de puntos x 1, x 2 c (a, b), tales que x 1 < x 2 , se cumple que f(x 1) < f(x 2) • Una función f es DECRECIENTE en el intervalo (a, b) si para todos los pares de puntos x 1, x 2 c (a, b), tales que x 1 < x 2 , se cumple que f(x 1) > f(x 2) • Una función f es CRECIENTE / DECRECIENTE en un punto xo c (a, b) si y sólo so existe un entorno simétrico de xo en el cual la función es CRECIENTE / DECRECIENTE. • • • TEOREMA Sea f una función definida en ( a, b) y xo c (a, b). Entonces: Si f ‘ (xo) > 0 la función es estrictamente CRECIENTE en xo. Si f ‘ (xo) < 0 la función es estrictamente DECRECIENTE en xo. @ Angel Prieto Benito Apuntes 2º Bachillerato C. T. 7

MÁXIMOS Y MÍNIMOS • Una función f tiene un máximo relativo en x=xo si existe un entorno reducido de xo de forma que f(x) < f(xo) para todo x perteneciente a dicho entorno. • Una función f tiene un mínimo relativo en x=xo si existe un entorno reducido de xo de forma que f(x) > f(xo) para todo x perteneciente a dicho entorno. • TEOREMA • Si f tiene un extremo relativo en x=xo y existe f ‘(x), entonces • Sea f una función definida en (a, b) y con derivada segunda en este intervalo y sea xo c (a, b) tal que f ‘ (xo) = 0 • Si f ”(xo) > 0, entonces f tiene en xo un MÍNIMO RELATIVO. • Si f ”(xo) < 0, entonces f tiene en xo un MÁXIMO RELATIVO. @ Angel Prieto Benito Apuntes 2º Bachillerato C. T. f ‘ (x) = 0 8

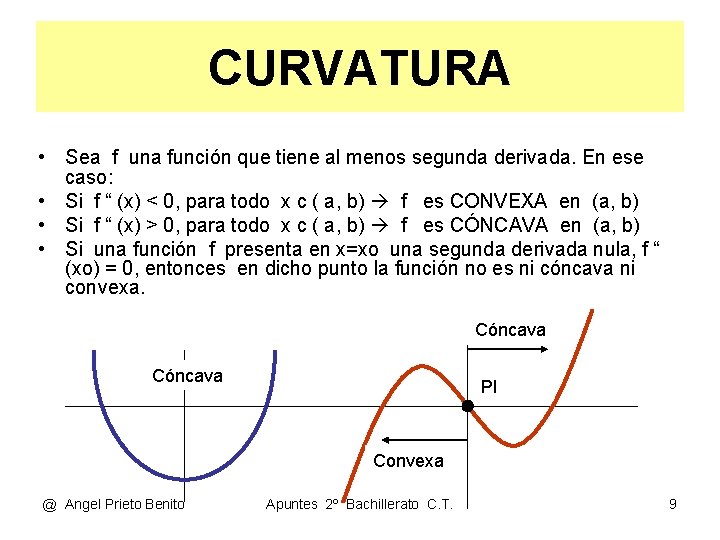
CURVATURA • Sea f una función que tiene al menos segunda derivada. En ese caso: • Si f “ (x) < 0, para todo x c ( a, b) f es CONVEXA en (a, b) • Si f “ (x) > 0, para todo x c ( a, b) f es CÓNCAVA en (a, b) • Si una función f presenta en x=xo una segunda derivada nula, f “ (xo) = 0, entonces en dicho punto la función no es ni cóncava ni convexa. Cóncava PI Convexa @ Angel Prieto Benito Apuntes 2º Bachillerato C. T. 9

PUNTOS DE INFLEXIÓN • Una función continua f tiene un PUNTO DE INFLEXIÓN en x= xo , si en ese punto la función cambia su curvatura, es decir si pasa de cóncava a convexa o viceversa. • Si f presenta un punto de inflexión en x=xo f “ (xo) = 0 • Pero si se cumple que f “(xo) = 0, no siempre en x= xo hay un P. I. • • TEOREMA Dada una función f y un punto xo perteneciente a su dominio, si se verifica que f “(xo) = 0 y f ‘’‘ (xo) <> 0 , entonces f posee en x=xo un PUNTO DE INFLEXIÓN. @ Angel Prieto Benito Apuntes 2º Bachillerato C. T. 10

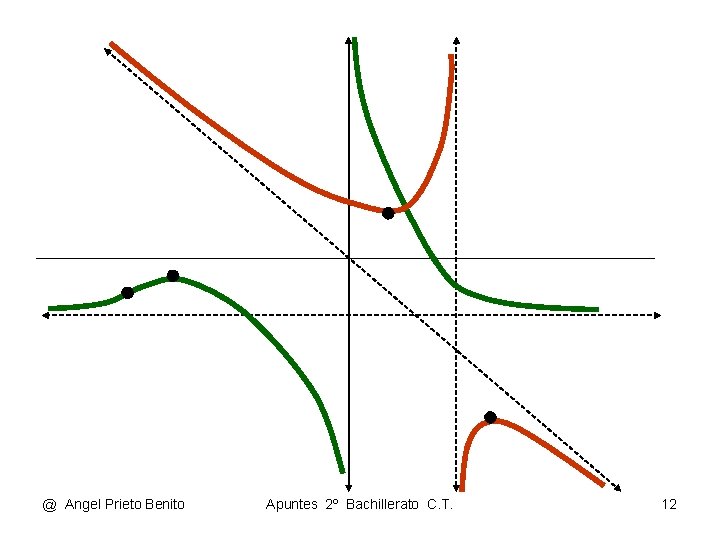
ASÍNTOTAS • La recta x = a es una asíntota vertical de la función f si: Lím x a • • • f(x) = ± oo La recta y = b es una asíntota horizontal de la función f si: • • Lím f(x) = b x ± oo • La recta y = m. x + n es una asíntota oblicua de la función f si: • • • f(x) Lím ------ = m x ± oo x @ Angel Prieto Benito y Lím [ f(x) – m. x ] = n x ± oo Apuntes 2º Bachillerato C. T. 11

@ Angel Prieto Benito Apuntes 2º Bachillerato C. T. 12