A Quick Note on Useful Algorithmic Strategies KunMao

A Quick Note on Useful Algorithmic Strategies Kun-Mao Chao (趙坤茂) Department of Computer Science and Information Engineering National Taiwan University, Taiwan WWW: http: //www. csie. ntu. edu. tw/~kmchao

Greedy Algorithm • A greedy method always makes a locally optimal (greedy) choice. – the greedy-choice property: a globally optimal solution can be reached by a greedy choice. – optimal substructures 2

Huffman Codes (1952) David Huffman (August 9, 1925 – October 7, 1999) 3

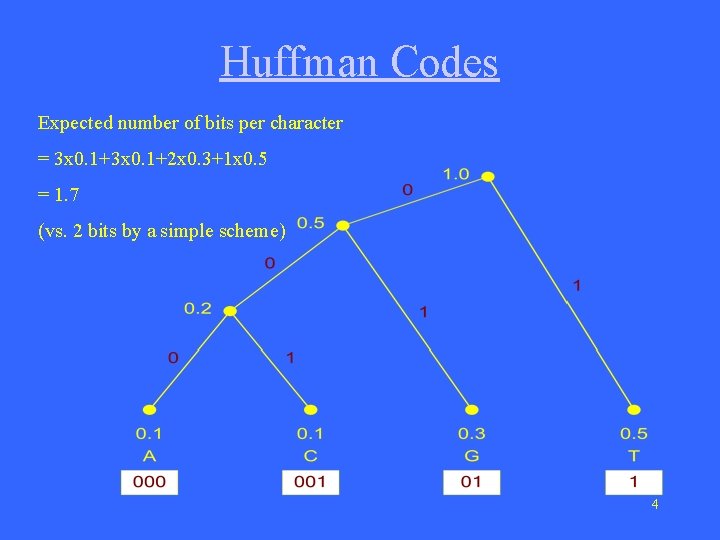
Huffman Codes Expected number of bits per character = 3 x 0. 1+2 x 0. 3+1 x 0. 5 = 1. 7 (vs. 2 bits by a simple scheme) 4

An example Sequence: GTTGTTATCGTTTATGTGGC By Huffman Coding: 011100010010111100010110101001 20 characters; 34 bits in total 5

Divide-and-Conquer 1. Divide the problem into smaller subproblems. 2. Conquer each subproblem recursively. 3. Combine the solutions to the child subproblems into the solution for the parent problem. 6

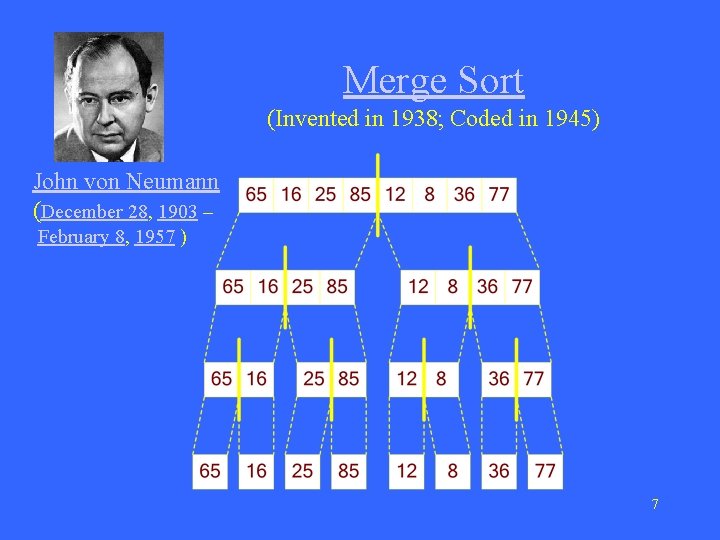
Merge Sort (Invented in 1938; Coded in 1945) John von Neumann (December 28, 1903 – February 8, 1957 ) 7

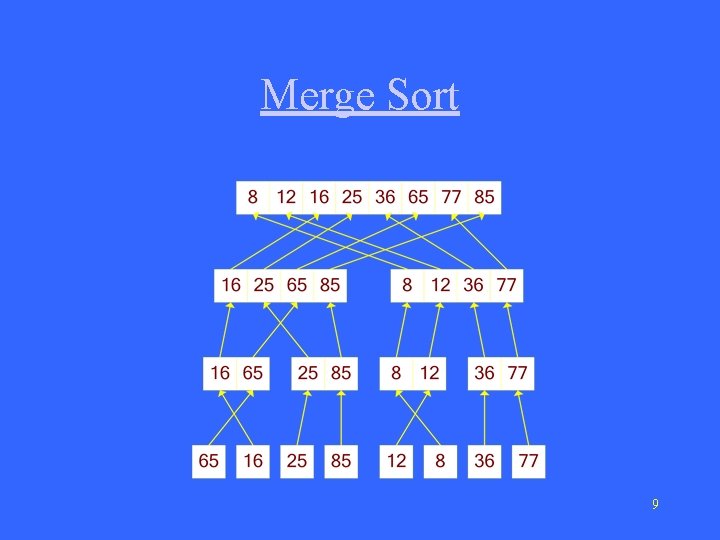
Merge Sort (Merge two solutions into one. ) 8

Merge Sort 9

Dynamic Programming • Dynamic programming is a class of solution methods for solving sequential decision problems with a compositional cost structure. • Richard Bellman was one of the principal founders of this approach. Richard Ernest Bellman (1920– 1984) 10

Two key ingredients • Two key ingredients for an optimization problem to be suitable for a dynamicprogramming solution: 1. optimal substructures 2. overlapping subproblems Subproblems are dependent. Each substructure is optimal. (otherwise, a divide-andconquer approach is the (Principle of optimality) 11 choice. )

Three basic components • The development of a dynamicprogramming algorithm has three basic components: – The recurrence relation (for defining the value of an optimal solution); – The tabular computation (for computing the value of an optimal solution); – The traceback (for delivering an optimal solution). 12

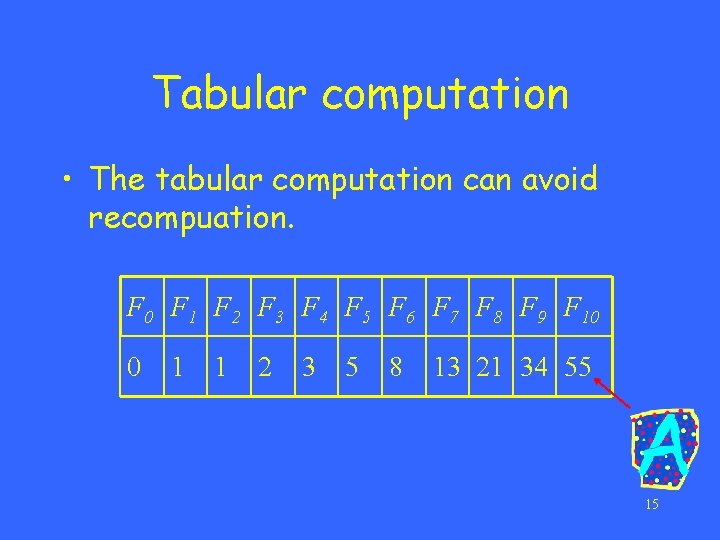
Fibonacci numbers The Fibonacci numbers are defined by the following recurrence: F =0 0 F =1 1 F = F - + F - for i>1. i i 1 i 2 Leonardo of Pisa (c. 1170 – c. 1250) 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, . . . 13

How to compute F 10？ F 10 F 9 F 8 F 7 …… F 7 F 6 14

Tabular computation • The tabular computation can avoid recompuation. F 0 F 1 F 2 F 3 F 4 F 5 F 6 F 7 F 8 F 9 F 10 0 1 1 2 3 5 8 13 21 34 55 15

Longest increasing subsequence(LIS) • The longest increasing subsequence is to find a longest increasing subsequence of a given sequence of distinct integers a 1 a 2…an. e. g. 9 2 5 3 7 11 8 10 13 6 2 3 7 5 7 10 13 9 7 11 10 3 5 11 13 are increasing subsequences. We want to find a longest one. are not increasing subsequences. 16

A naive approach for LIS • Let L[i] be the length of a longest increasing subsequence ending at position i. L[i] = 1 + max j = 0. . i-1{L[j] | aj < ai} (use a dummy a 0 = minimum, and L[0]=0) 9 2 5 3 7 11 8 10 13 6 L[i] 1 1 2 2 3 4 ? 17

A naive approach for LIS L[i] = 1 + max j = 0. . i-1 {L[j] | aj < ai} 9 2 5 3 7 11 8 10 13 6 L[i] 1 1 2 2 3 4 4 5 6 3 The maximum length The subsequence 2, 3, 7, 8, 10, 13 is a longest increasing subsequence. This method runs in O(n 2) time. 18

An O(n log n) method for LIS • Define Best. End[k] to be the smallest number of an increasing subsequence of length k. 9 2 5 3 7 11 8 10 13 9 2 2 3 7 11 2 3 7 8 10 13 2 5 2 3 7 6 Best. End[1] Best. End[2] Best. End[3] Best. End[4] Best. End[5] Best. End[6] 19

An O(n log n) method for LIS • Define Best. End[k] to be the smallest number of an increasing subsequence of length k. 9 2 5 3 7 11 8 10 13 9 2 2 3 7 11 2 3 7 8 10 13 2 5 2 3 7 For each position, we perform a binary search to update Best. End. Therefore, the running time is O(n log n). 6 2 3 6 8 10 13 Best. End[1] Best. End[2] Best. End[3] Best. End[4] Best. End[5] Best. End[6] 20

Longest Common Subsequence (LCS) • A subsequence of a sequence S is obtained by deleting zero or more symbols from S. For example, the following are all subsequences of “president”: pred, sdn, predent. • The longest common subsequence problem is to find a maximum-length common subsequence between two sequences. 23

LCS For instance, Sequence 1: president Sequence 2: providence Its LCS is priden. president providence 24

LCS Another example: Sequence 1: algorithm Sequence 2: alignment One of its LCS is algm. a l g o r i t h m a l i g n m e n t 25

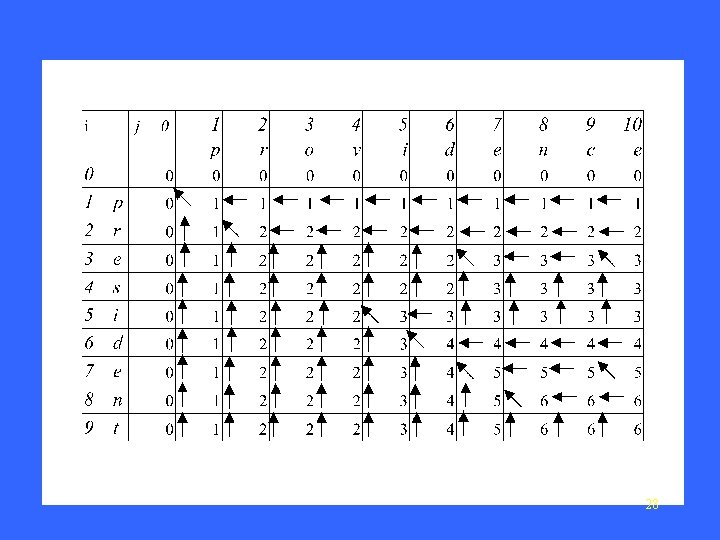
How to compute LCS? • Let A=a 1 a 2…am and B=b 1 b 2…bn. • len(i, j): the length of an LCS between a 1 a 2…ai and b 1 b 2…bj • With proper initializations, len(i, j)can be computed as follows. 26

27

28

29

30

Longest Common Increasing Subsequence • Proposed by Yang, Huang and Chao – IPL 2005 • Improvement for some special case: – Katriel and Kutz (March 2005) – Chan, Zhang, Fung, Ye and Zhu (ISAAC 2005) 31