A NOTE ON USEFUL ALGORITHMIC STRATEGIES KunMao Chao

A NOTE ON USEFUL ALGORITHMIC STRATEGIES Kun-Mao Chao (趙坤茂) Department of Computer Science and Information Engineering National Taiwan University, Taiwan WWW: http: //www. csie. ntu. edu. tw/~kmchao

Greedy Algorithm 2 A greedy method always makes a locally optimal (greedy) choice. the greedy-choice property: a globally optimal solution can be reached by a greedy choice. optimal substructures

Huffman Codes (1952) David Huffman (August 9, 1925 – October 7, 1999) 3

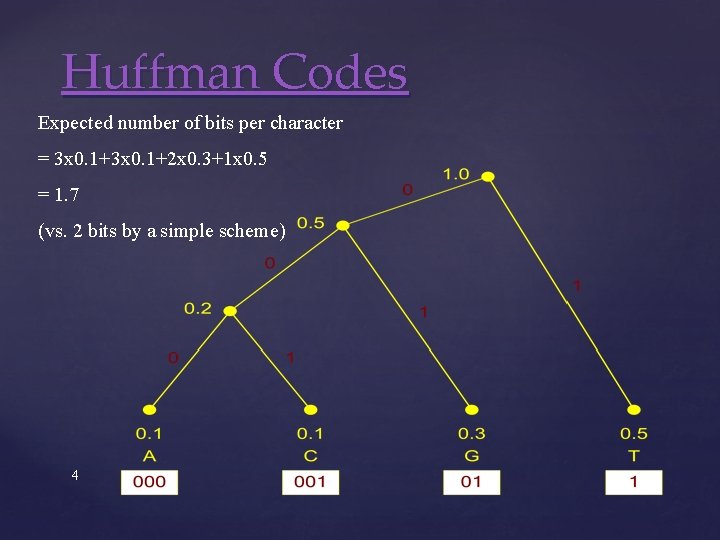
Huffman Codes Expected number of bits per character = 3 x 0. 1+2 x 0. 3+1 x 0. 5 = 1. 7 (vs. 2 bits by a simple scheme) 4

An example 5 Sequence: GTTGTTATCGTTTATGTGGC By Huffman Coding: 011100010010111100010110101001 20 characters; 34 bits in total

Divide-and-Conquer 6 1. 2. 3. Divide the problem into smaller subproblems. Conquer each subproblem recursively. Combine the solutions to the child subproblems into the solution for the parent problem.

Merge Sort (Invented in 1938; Coded in 1945) John von Neumann (December 28, 1903 – February 8, 1957 ) 7

Merge Sort (Merge two solutions into one. ) 8

Merge Sort 9

Dynamic Programming 10 Dynamic programming is a class of solution methods for solving sequential decision problems with a compositional cost structure. Richard Bellman was one of the principal founders of this approach. Richard Ernest Bellman (1920– 1984)

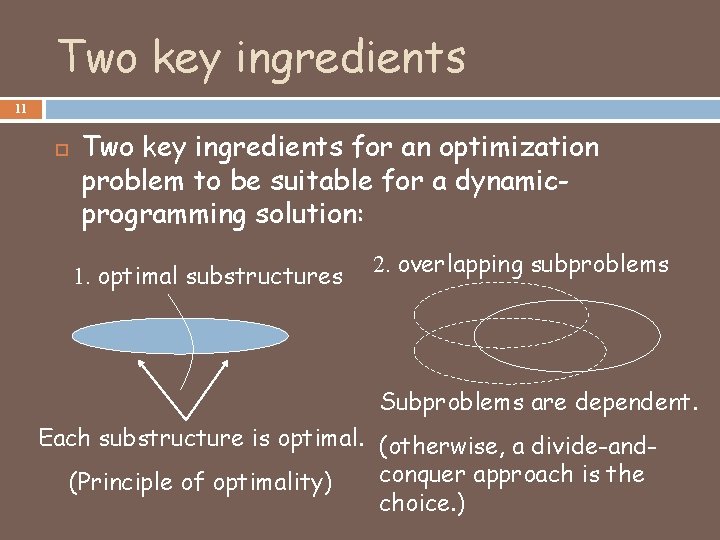
Two key ingredients 11 Two key ingredients for an optimization problem to be suitable for a dynamicprogramming solution: 1. optimal substructures 2. overlapping subproblems Subproblems are dependent. Each substructure is optimal. (otherwise, a divide-andconquer approach is the (Principle of optimality) choice. )

Three basic components 12 The development of a dynamic-programming algorithm has three basic components: The recurrence relation (for defining the value of an optimal solution); The tabular computation (for computing the value of an optimal solution); The traceback (for delivering an optimal solution).

Fibonacci numbers 13 The Fibonacci numbers are defined by the following recurrence: F =0 0 F =1 1 F = F - + F - for i>1. i i 1 i 2 Leonardo of Pisa (c. 1170 – c. 1250) 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, . . .

How to compute F 10？ 14 F 10 F 9 F 8 F 7 …… F 7 F 6

Tabular computation 15 The tabular computation can avoid recompuation. F 0 F 1 F 2 F 3 F 4 F 5 F 6 F 7 F 8 F 9 F 10 0 1 1 2 3 5 8 13 21 34 55

Longest increasing subsequence(LIS) 16 The longest increasing subsequence is to find a longest increasing subsequence of a given sequence of distinct integers a 1 a 2…an. e. g. 9 2 5 3 7 11 8 10 13 6 2 3 7 5 7 10 13 9 7 11 3 5 11 13 are increasing subsequences. We want to find a longest one. are not increasing subsequences.

A naive approach for LIS 17 Let L[i] be the length of a longest increasing subsequence ending at position i. L[i] = 1 + max j = 0. . i-1{L[j] | aj < ai} (use a dummy a 0 = minimum, and L[0]=0) 9 2 5 3 7 11 8 10 13 6 L[i] 1 1 2 2 3 4 ?

A naive approach for LIS 18 L[i] = 1 + max j = 0. . i-1 {L[j] | aj < ai} 9 2 5 3 7 11 8 10 13 6 L[i] 1 1 2 2 3 4 4 5 6 3 The maximum length The subsequence 2, 3, 7, 8, 10, 13 is a longest increasing subsequence. This method runs in O(n 2) time.

An O(n log n) method for LIS 19 Define Best. End[k] to be the smallest number of an increasing subsequence of length k. 9 2 5 3 7 11 8 10 13 9 2 2 3 7 11 2 3 7 8 10 13 2 5 2 3 7 6 Best. End[1] Best. End[2] Best. End[3] Best. End[4] Best. End[5] Best. End[6]

An O(n log n) method for LIS Define Best. End[k] to be the smallest number of an increasing subsequence of length k. 9 2 5 3 7 11 8 10 13 9 2 2 3 7 11 2 3 7 8 10 13 2 5 2 3 7 For each position, we perform a binary search to update Best. End. Therefore, the running time is O(n log n). 6 2 3 6 8 10 13 Best. End[1] Best. End[2] Best. End[3] Best. End[4] Best. End[5] Best. End[6] 20 The subsequence 2, 3, 7, 8, 10, 13 is a longest increasing subsequence.

Binary search 21 Given an ordered sequence x 1 x 2. . . xn, where x 1<x 2<. . . <xn, and a number y, a binary search finds the largest xi such that xi< y in O(log n) time. n/2 n n/4 . . .

Binary search 22 How many steps would a binary search reduce the problem size to 1? n n/2 n/4 n/8 n/16. . . 1 How many steps? O(log n) steps.

Longest Common Subsequence (LCS) 23 A subsequence of a sequence S is obtained by deleting zero or more symbols from S. For example, the following are all subsequences of “president”: pred, sdn, predent. The longest common subsequence problem is to find a maximum-length common subsequence between two sequences.

LCS 24 For instance, Sequence 1: president Sequence 2: providence Its LCS is priden. president providence

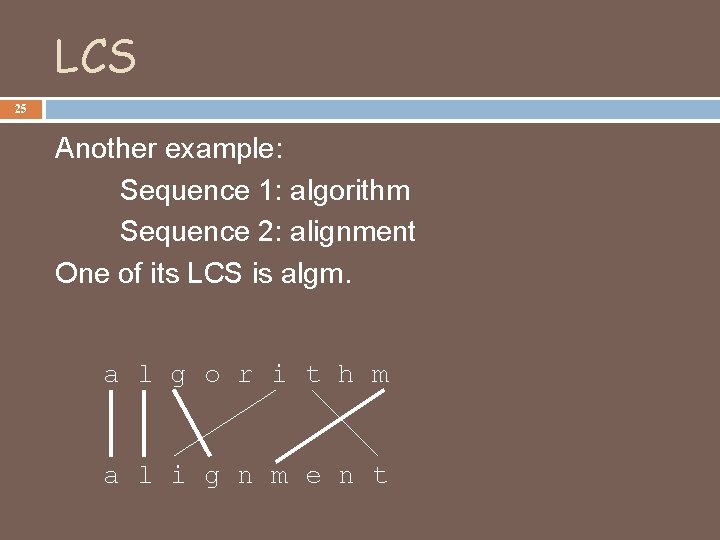
LCS 25 Another example: Sequence 1: algorithm Sequence 2: alignment One of its LCS is algm. a l g o r i t h m a l i g n m e n t

How to compute LCS? 26 Let A=a 1 a 2…am and B=b 1 b 2…bn. len(i, j): the length of an LCS between a 1 a 2…ai and b 1 b 2…bj With proper initializations, len(i, j)can be computed as follows.

27

28

29

30

Longest Common Increasing Subsequence 31 Proposed by Yang, Huang and Chao IPL 2005 9 2 5 3 7 11 8 10 13 6 6 5 2 8 3 7 4 10 1 13