Algorithmic Foundations COMP 108 Algorithmic Foundations Algorithm efficiency

Algorithmic Foundations COMP 108 Algorithmic Foundations Algorithm efficiency Prudence Wong

Learning outcomes Ø Algorithmic Foundations COMP 108 Able to carry out simple asymptotic analysis of algorithms 2 (Efficiency)

Time Complexity Analysis Algorithmic Foundations COMP 108 How fast is the algorithm? Code the algorithm and run the program, then measure the running time 1. Depend on the speed of the computer 2. Waste time coding and testing if the algorithm is slow Identify some important operations/steps and count how many times these operations/steps needed to be executed 3 (Efficiency)

Time Complexity Analysis Algorithmic Foundations COMP 108 How to measure efficiency? Number of operations usually expressed in terms of input size Ø If we doubled/trebled the input size, how much longer would the algorithm take? 4 (Efficiency)

Why efficiency matters? Algorithmic Foundations COMP 108 Ø speed of computation by hardware has been improved Ø efficiency still matters Ø ambition for computer applications grow with computer power Ø demand a great increase in speed of computation 5 (Efficiency)

Algorithmic Foundations COMP 108 Amount of data handled matches speed increase? When computation speed vastly increased, can we handle much more data? Suppose • an algorithm takes n 2 comparisons to sort n numbers • we need 1 sec to sort 5 numbers (25 comparisons) • computing speed increases by factor of 100 Using 1 sec, we can now perform 100 x 25 comparisons, i. e. , to sort 50 numbers With 100 times speedup, only sort 10 times more numbers! 6 (Efficiency)

Algorithmic Foundations COMP 108 Time/Space Complexity Analysis Important operation of summation: addition How many additions this algorithm requires? input n sum = 0 for i = 1 to n do begin sum = sum + i end output sum We need n additions (depend on the input size n) We need 3 variables n, sum, & i needs 3 memory space In other cases, space complexity may depend on the input size n 7 (Efficiency)

Algorithmic Foundations COMP 108 Look for improvement Mathematical formula gives us an alternative way to find the sum of first n numbers: input n sum = n*(n+1)/2 output sum 1 + 2 +. . . + n = n(n+1)/2 We only need 3 operations: 1 addition, 1 multiplication, and 1 division (no matter what the input size n is) 8 (Efficiency)

Improve Searching Algorithmic Foundations COMP 108 We've learnt sequential search and it takes n comparisons in the worst case. If the numbers are pre-sorted, then we can improve the time complexity of searching by binary search. 9 (Efficiency)

Binary Search Algorithmic Foundations COMP 108 more efficient way of searching when the sequence of numbers is pre-sorted Input: a sequence of n sorted numbers a 1, a 2, …, an in ascending order and a number X Idea of algorithm: Ø Ø Ø compare X with number in the middle then focus on only the first half or the second half (depend on whether X is smaller or greater than the middle number) reduce the amount of numbers to be searched by half 10 (Efficiency)

Binary Search (2) 3 7 11 12 Algorithmic Foundations COMP 108 To find 24 15 19 24 33 41 55 24 10 nos X 19 24 33 41 55 24 19 24 24 found! 11 (Efficiency)

Binary Search (3) 3 7 11 12 Algorithmic Foundations COMP 108 To find 30 15 19 24 33 41 55 30 10 nos X 19 24 33 41 55 30 19 24 30 not found! 12 (Efficiency)

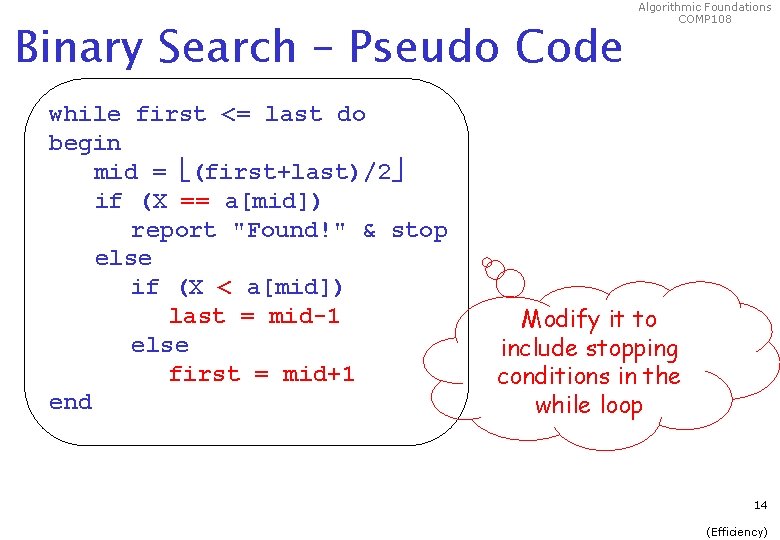
Binary Search – Pseudo Code Algorithmic Foundations COMP 108 first = 1 last = n while (first <= last) do begin // check with no. in middle end report "Not Found!" is the floor function, truncates the decimal part mid = (first+last)/2 if (X == a[mid]) report "Found!" & stop else if (X < a[mid]) last = mid-1 else first = mid+1 13 (Efficiency)

Binary Search – Pseudo Code while first <= last do begin mid = (first+last)/2 if (X == a[mid]) report "Found!" & stop else if (X < a[mid]) last = mid-1 else first = mid+1 end Algorithmic Foundations COMP 108 Modify it to include stopping conditions in the while loop 14 (Efficiency)

Number of Comparisons Best case: X is the number in the middle 1 comparison Worst case: at most log 2 n +1 comparisons Why? Every comparison reduces the amount of numbers by at least half E. g. , 16 8 4 2 1 Algorithmic Foundations COMP 108 first=1, last=n while (first <= last) do begin mid = (first+last)/2 if (X == a[mid]) report "Found!" & stop else if (X < a[mid]) last = mid-1 else first = mid+1 end report "Not Found!" 15 (Efficiency)

Algorithmic Foundations COMP 108 Time complexity - Big O notation …

Note on Logarithm Algorithmic Foundations COMP 108 Logarithm is the inverse of the power function log 2 2 x = x For example, log 2 x*y = log 2 x + log 2 y log 2 4*8 = log 2 4 + log 2 8 = 2+3 = 5 log 2 1 = log 2 20 = 0 log 2 2 = log 2 21 = 1 log 2 4 = log 2 22 = 2 log 2 16*16 = log 2 16 + log 2 16 = 8 log 2 x/y = log 2 x - log 2 y log 2 16 = log 2 24 = 4 log 2 32/8 = log 2 32 - log 2 8 = 5 -3 = 2 log 2 1/4 = log 2 1 - log 2 4 = 0 -2 = -2 log 2 256 = log 2 28 = 8 log 2 1024 = log 2 210 = 10 17 (Efficiency)

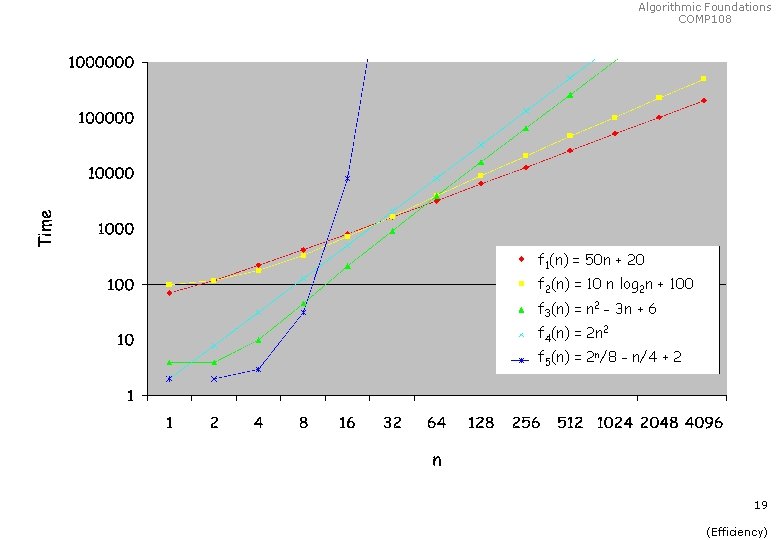
Algorithmic Foundations COMP 108 Which algorithm is the fastest? Consider a problem that can be solved by 5 algorithms A 1, A 2, A 3, A 4, A 5 using different number of operations (time complexity). f 1(n) = 50 n + 20 f 3(n) = n 2 - 3 n + 6 f 5(n) = 2 n/8 - n/4 + 2 f 5(n) f 2(n) = 10 n log 2 n + 100 f 4(n) = 2 n 2 f 3(n) Depends on the size of the input! f 1(n) 18 (Efficiency)

Algorithmic Foundations COMP 108 f 1(n) = 50 n + 20 f 2(n) = 10 n log 2 n + 100 f 3(n) = n 2 - 3 n + 6 f 4(n) = 2 n 2 f 5(n) = 2 n/8 - n/4 + 2 19 (Efficiency)

What do we observe? Ø Algorithmic Foundations COMP 108 There is huge difference between Ø functions involving powers of n (e. g. , n, n 2, called polynomial functions) and Ø functions involving powering by n (e. g. , 2 n, 3 n, called exponential functions) Ø Among polynomial functions, those with same order of power are more comparable Ø e. g. , f 3(n) = n 2 - 3 n + 6 and f 4(n) = 2 n 2 20 (Efficiency)

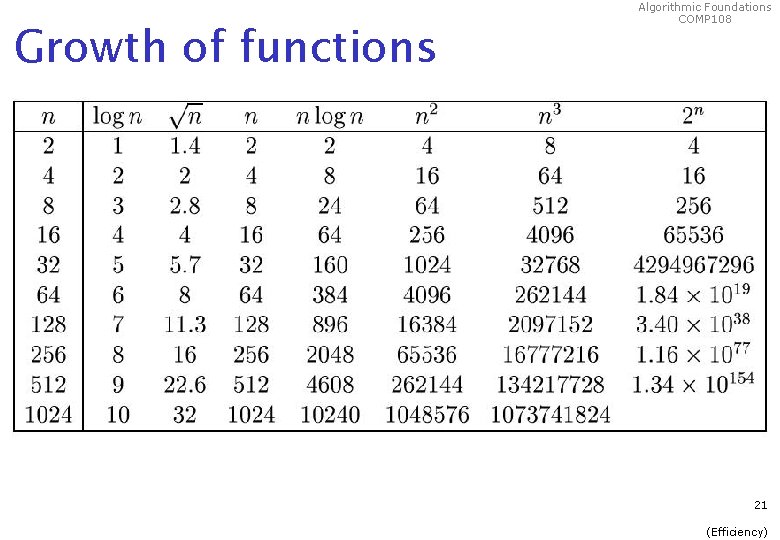
Growth of functions Algorithmic Foundations COMP 108 21 (Efficiency)

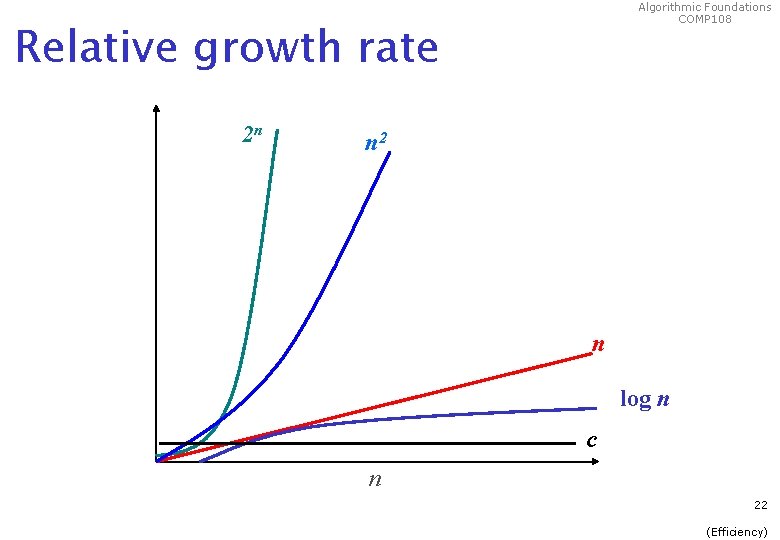
Algorithmic Foundations COMP 108 Relative growth rate 2 n n 2 n log n c n 22 (Efficiency)

Algorithmic Foundations COMP 108 Hierarchy of functions Ø We can define a hierarchy of functions each having a greater order of growth than its predecessor: 1 constant Ø log n logarithmic n n 2 n 3. . . nk. . . 2 n polynomial exponential We can further refine the hierarchy by inserting n log n between n and n 2, n 2 log n between n 2 and n 3, and so on. 23 (Efficiency)

Hierarchy of functions (2) 1 constant log n logarithmic Algorithmic Foundations COMP 108 n n 2 n 3. . . nk. . . 2 n polynomial exponential Note: as we move from left to right, successive functions have greater order of growth than the previous ones. As n increases, the values of the later functions increase more rapidly than the earlier ones. Relative growth rates increase 24 (Efficiency)

Hierarchy of functions (3) What about log 3 n & n? Which is higher in hierarchy? Algorithmic Foundations COMP 108 (log n)3 Remember: n = 2 log n So we are comparing (log n)3 & 2 log n log 3 n is lower than n in the hierarchy Similarly, logk n is lower than n in the hierarchy, for any constant k 25 (Efficiency)

Algorithmic Foundations COMP 108 Hierarchy of functions (4) 1 constant Ø logarithmic n n 2 n 3. . . nk. . . 2 n polynomial exponential Now, when we have a function, we can classify the function to some function in the hierarchy: Ø Ø log n For example, f(n) = 2 n 3 + 5 n 2 + 4 n + 7 The term with the highest power is 2 n 3. The growth rate of f(n) is dominated by n 3. This concept is captured by Big-O notation 26 (Efficiency)

Big-O notation Algorithmic Foundations COMP 108 f(n) = O(g(n)) [read as f(n) is of order g(n)] Ø Roughly speaking, this means f(n) is at most a constant times g(n) for all large n Ø Examples Ø 2 n 3 = O(n 3) Ø 3 n 2 = O(n 2) Ø 2 n log n = O(n log n) Ø n 3 + n 2 = O(n 3) 27 (Efficiency)

Algorithmic Foundations COMP 108 Exercise Determine the order of growth of the following functions. 1. n 3 + 3 n 2 + 3 O(n 3) 2. 4 n 2 log n + n 3 + 5 n 2 + n O(n 3) 3. 2 n 2 + n 2 log n 4. 6 n 2 + 2 n O(n 2 log n) O(2 n) Look for the term highest in the hierarchy 28 (Efficiency)

Algorithmic Foundations COMP 108 More Exercise Are the followings correct? 1. n 2 log n + n 3 + 3 n 2 + 3 O(n 2 log n)? O(n 3) 2. n + 1000 O(n)? 3. 6 n 20 + 2 n O(n 20)? YES 4. n 3 + 5 n 2 log n + n O(n 2 log n) ? O(n 3) O(2 n) 29 (Efficiency)

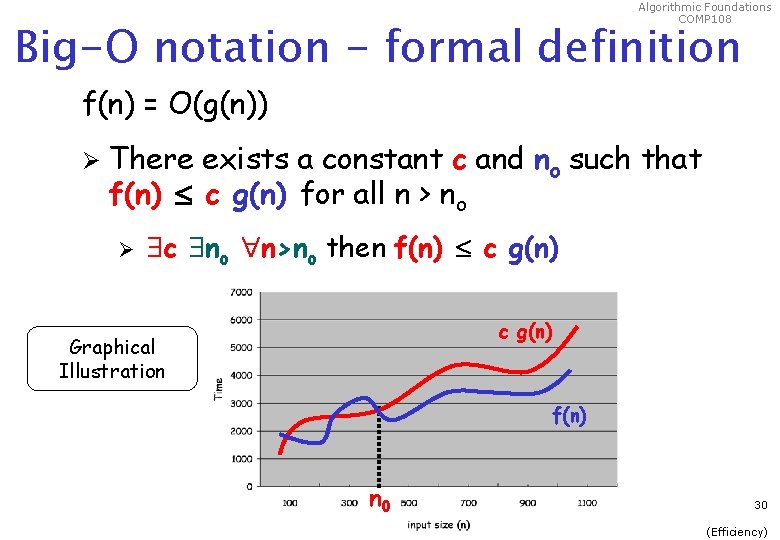
Algorithmic Foundations COMP 108 Big-O notation - formal definition f(n) = O(g(n)) Ø There exists a constant c and no such that f(n) c g(n) for all n > no Ø c no n>no then f(n) c g(n) Graphical Illustration f(n) n 0 30 (Efficiency)

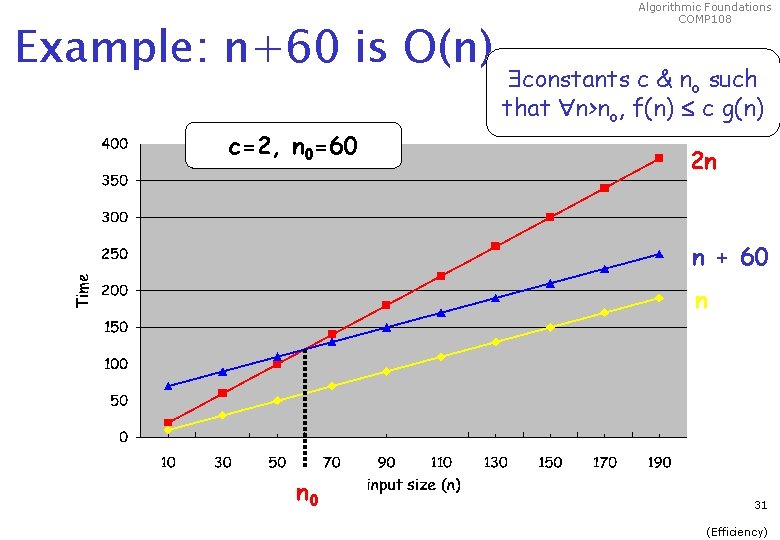
Example: n+60 is O(n) c=2, n 0=60 Algorithmic Foundations COMP 108 constants c & no such that n>no, f(n) c g(n) 2 n n + 60 n n 0 31 (Efficiency)

Which one is the fastest? Algorithmic Foundations COMP 108 Usually we are only interested in the asymptotic time complexity Ø i. e. , when n is large O(log n) < O(log 2 n) < O(n) < O(n log n) < O(n 2) < O(2 n) 32 (Efficiency)

Algorithmic Foundations COMP 108 Proof of order of growth Ø Prove ü that 2 n 2 + 4 n is O(n 2) Since n n 2 n≥ 1, we have 2 n 2 + 4 n 2 = 6 n 2 ü Note: plotting a graph is NOT a proof n≥ 1. Therefore, by definition, 2 n 2 + 4 n is O(n 2). Ø Alternatively, ü Since 4 n n 2 n≥ 4, we have 2 n 2 + 4 n 2 n 2 + n 2 = 3 n 2 ü n≥ 4. Therefore, by definition, 2 n 2 + 4 n is O(n 2). 33 (Efficiency)

Proof of order of growth (2) Ø Prove ü Algorithmic Foundations COMP 108 that n 3 + 3 n 2 + 3 is O(n 3) Since n 2 n 3 and 1 n 3 n≥ 1, we have n 3 + 3 n 2 + 3 n 3 + 3 n 3 = 7 n 3 ü n≥ 1. Therefore, by definition, n 3 + 3 n 2 + 3 is O(n 3). Ø Alternatively, ü Since 3 n 2 n 3 n≥ 3, and 3 n 3 n≥ 2 we have n 3 + 3 n 2 + 3 3 n 3 ü n≥ 3. Therefore, by definition, n 3 + 3 n 2 + 3 is O(n 3). 34 (Efficiency)

Algorithmic Foundations COMP 108 Challenges Prove the order of growth 1. 2 n 3 + n 2 + 4 n + 4 is O(n 3) 2 n 3 = 2 n 3 b) n 2 n 3 c) 4 n n 3 d) 4 n 3 2 n 3 + n 2 + 4 n a) 2 n 3 = 2 n 3 b) n 2 n 3 c) 4 n 3 d) 4 4 n 3 2 n 3+n 2+4 n+4 n n 1 n 2 + 4 5 n 3 n 2 2 n 2 + 2 n is O(2 n) a) 2 n 2 2 n n 7 b) 2 n = 2 n n 2 n 2 + 2 n 2*2 n n n 1 n 1 11 n 3 n 1 a) 2 n 2 2*2 n b) 2 n = 2 n 2+2 n 3*2 n n 4 n n 4 n 7 35 (Efficiency)

Some algorithms we learnt Sum of 1 st n no. input n sum = n*(n+1)/2 output sum O(1) Algorithmic Foundations COMP 108 input n O(n) sum = 0 for i = 1 to n do begin sum = sum + i end output sum Min value among n no. loc = 1 for i = 2 to n do if (a[i] < a[loc]) then loc = i output a[loc] O(n) 36 (Efficiency)

Time complexity of this? for i = 1 to 2 n do for j = 1 to n do x = x + 1 Algorithmic Foundations COMP 108 O(n 2) The outer loop iterates for 2 n times. The inner loop iterates for n times for each i. Total: 2 n * n = 2 n 2. 37 (Efficiency)

What about this? O(log n) i = 1 count = 0 while i < n begin i = 2 * i count = count + 1 end output count Algorithmic Foundations COMP 108 suppose n=8 i count 1 0 1 2 3 4 8 2 3 (@ end of ) i count 1 2 3 4 5 1 2 4 8 16 32 0 1 2 3 4 5 (@ end of ) iteration suppose n=32 iteration 38 (Efficiency)