Algorithmic Foundations COMP 108 Algorithmic Foundations Basics Prudence

Algorithmic Foundations COMP 108 Algorithmic Foundations Basics Prudence Wong http: //www. csc. liv. ac. uk/~pwong/teaching/comp 108/201617

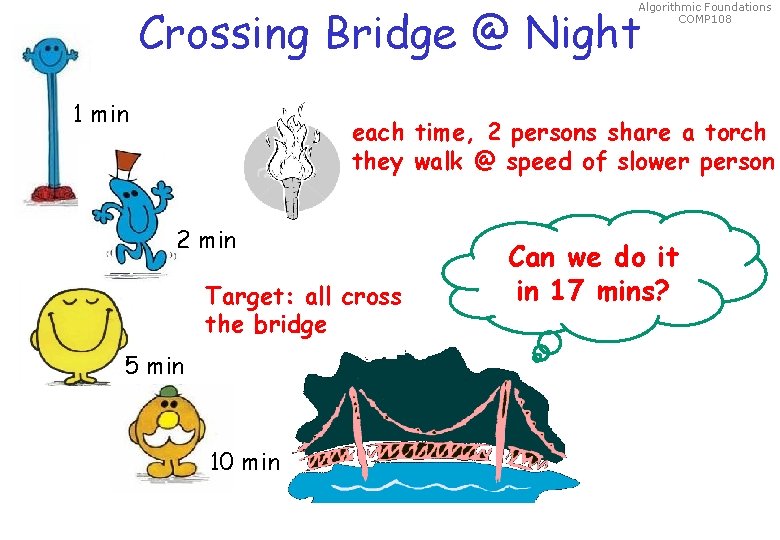
Algorithmic Foundations COMP 108 Crossing Bridge @ Night 1 min each time, 2 persons share a torch they walk @ speed of slower person 2 min Target: all cross the bridge 5 min 10 min Can we do it in 17 mins?

Module Information Algorithmic Foundations COMP 108 Professor Prudence Wong Rm 3. 18 Ashton Building, pwong@liverpool. ac. uk office hours: Tue 10 -11 am Demonstrators Mr Thomas Carroll, Mr Reino Niskanen References Main: Introduction to the Design and Analysis of Algorithms. A. V. Levitin. Addison Wesley. Reference: Introduction to Algorithms. T. H. Cormen, C. E. Leiserson, R. L. Rivest, C. Stein. The MIT Press 3 (Basics)

Module Information (2) Algorithmic Foundations COMP 108 Teaching, Assessments and Help 36 lectures, 11 tutorials 2 assessments (20%), 1 written exam (80%) Office hours, email Tutorials/Labs Location : Lecture Rooms (theoretical) or Lab (practical) Week 2: Theoretical – Lecture Rooms 4 (Basics)

Module Information (3) Ø Ø Ø Algorithmic Foundations COMP 108 Each assessment has two components Ø Tutorial participation (25%) Ø Class Test (75%) Assessment 1 Ø Tutorials 1 – 6 (Weeks 2 -7) Ø Class Test 1: Week 8, Thu 23 rd Mar Assessment 2 Ø Tutorials 7 – 11 (Weeks 8 -12) Ø Class Test 2: Week 12, Thu 11 th May 5 (Basics)

Why COMP 108? Algorithmic Foundations COMP 108 Pre-requisite for: COMP 202, COMP 218 (COMP 202 is pre-requisite for COMP 309) Algorithm design is a foundation for efficient and effective programs "Year 1 modules do not count towards honour classification…" (Career Services: Employers DO consider year 1 module results) 6 (Basics)

Aims Algorithmic Foundations COMP 108 Ø To give an overview of the study of algorithms in terms of their efficiency. What do we mean by good? Ø To introduce the standard algorithmic design paradigms employed in the development of efficient algorithmic solutions. How to achieve? Ø To describe the analysis of algorithms in terms of the use of formal models of Time and Space. Can we prove? 7 (Basics)

Algorithmic Foundations COMP 108 Ready to start … Learning outcomes Able to tell what an algorithm is & have some understanding why we study algorithms Ø Able to use pseudo code to describe algorithm

What is an algorithm? Algorithmic Foundations COMP 108 A sequence of precise and concise instructions that guide you (or a computer) to solve a specific problem Input Algorithm Output Daily life examples: cooking recipe, furniture assembly manual (What are input / output in each case? ) 9 (Basics)

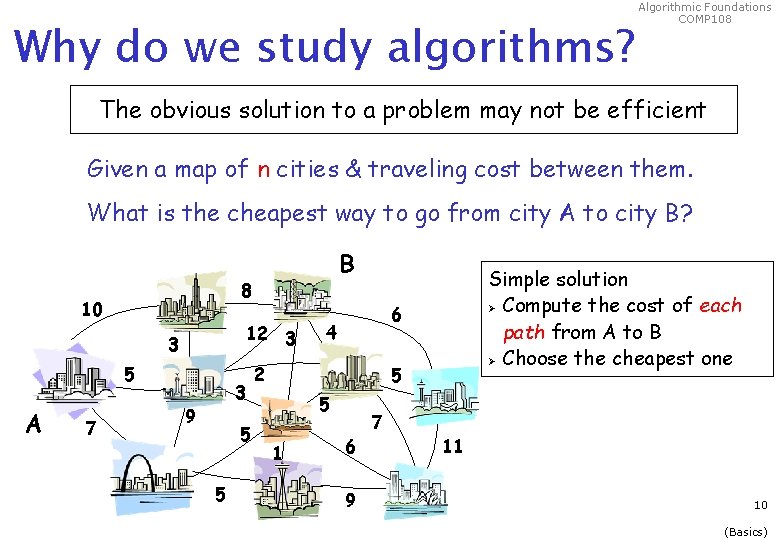
Why do we study algorithms? Algorithmic Foundations COMP 108 The obvious solution to a problem may not be efficient Given a map of n cities & traveling cost between them. What is the cheapest way to go from city A to city B? 8 10 12 3 3 5 A 7 B 3 9 5 5 Simple solution Ø Compute the cost of each path from A to B Ø Choose the cheapest one 6 4 2 5 5 1 6 9 7 11 10 (Basics)

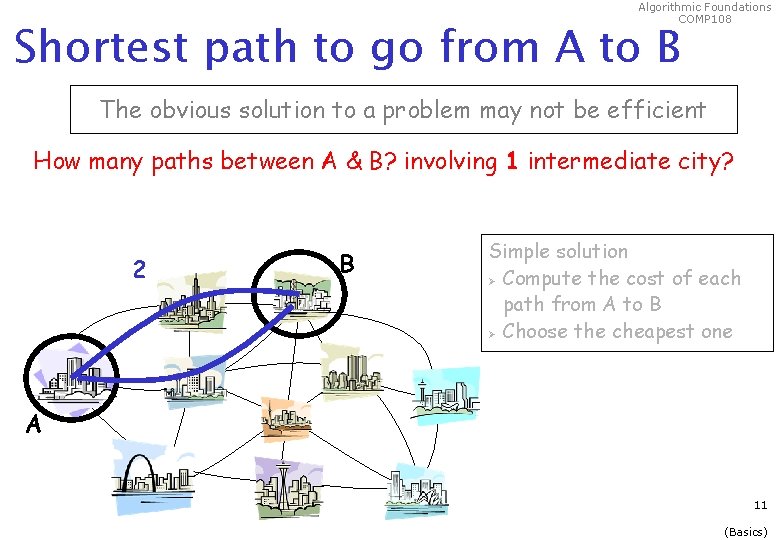
Algorithmic Foundations COMP 108 Shortest path to go from A to B The obvious solution to a problem may not be efficient How many paths between A & B? involving 1 intermediate city? 2 B Simple solution Ø Compute the cost of each path from A to B Ø Choose the cheapest one A 11 (Basics)

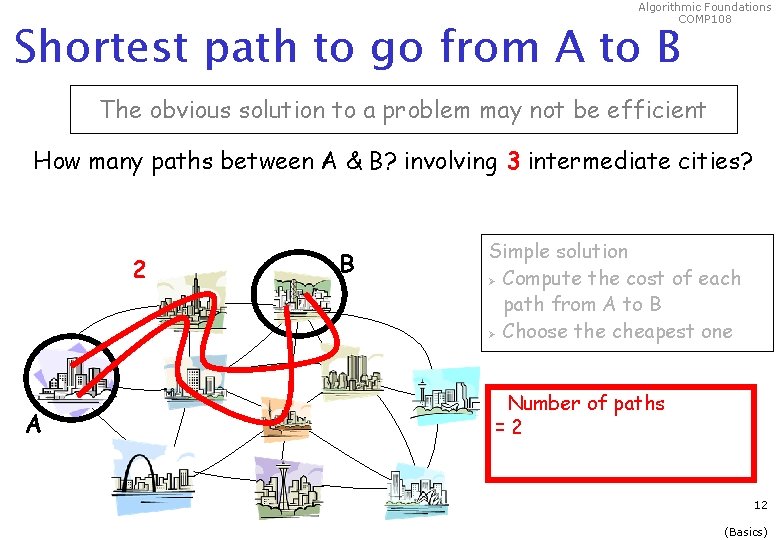
Algorithmic Foundations COMP 108 Shortest path to go from A to B The obvious solution to a problem may not be efficient How many paths between A & B? involving 3 intermediate cities? 2 A B Simple solution Ø Compute the cost of each path from A to B Ø Choose the cheapest one Number of paths =2 12 (Basics)

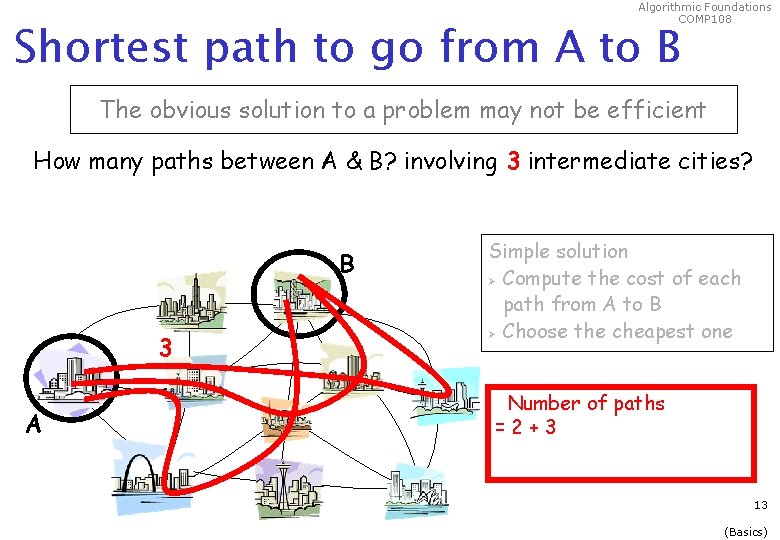
Algorithmic Foundations COMP 108 Shortest path to go from A to B The obvious solution to a problem may not be efficient How many paths between A & B? involving 3 intermediate cities? B 3 A Simple solution Ø Compute the cost of each path from A to B Ø Choose the cheapest one Number of paths =2+3 13 (Basics)

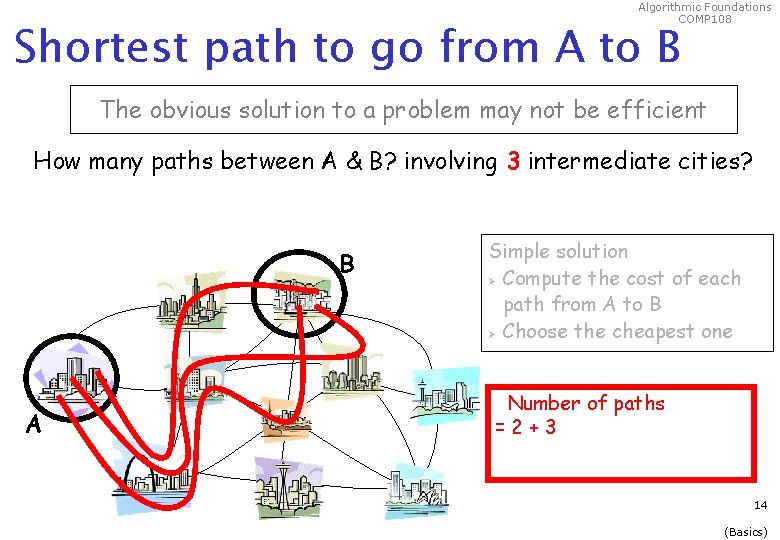
Algorithmic Foundations COMP 108 Shortest path to go from A to B The obvious solution to a problem may not be efficient How many paths between A & B? involving 3 intermediate cities? B A Simple solution Ø Compute the cost of each path from A to B Ø Choose the cheapest one Number of paths =2+3 14 (Basics)

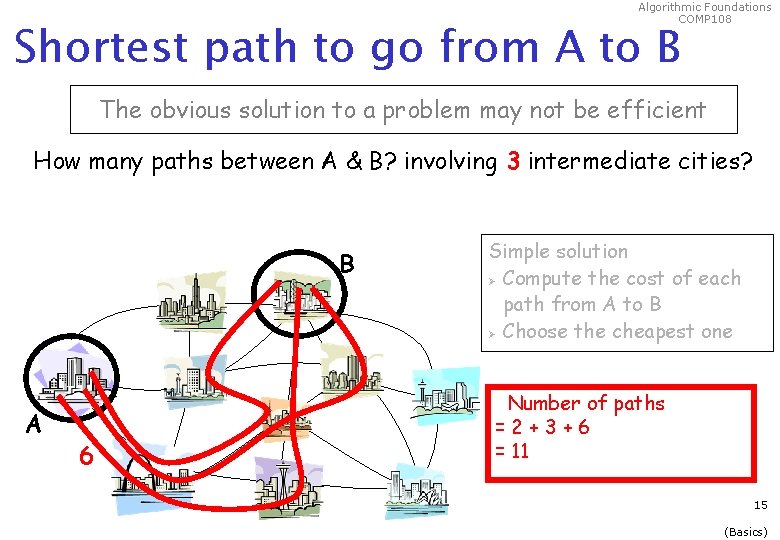
Algorithmic Foundations COMP 108 Shortest path to go from A to B The obvious solution to a problem may not be efficient How many paths between A & B? involving 3 intermediate cities? B A 6 Simple solution Ø Compute the cost of each path from A to B Ø Choose the cheapest one Number of paths =2+3+6 = 11 15 (Basics)

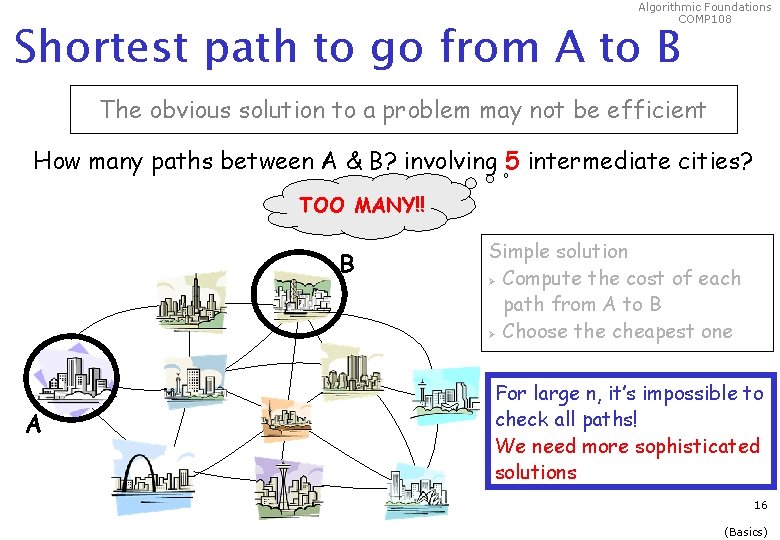
Algorithmic Foundations COMP 108 Shortest path to go from A to B The obvious solution to a problem may not be efficient How many paths between A & B? involving 5 intermediate cities? TOO MANY!! B A Simple solution Ø Compute the cost of each path from A to B Ø Choose the cheapest one For large n, it’s impossible to check all paths! We need more sophisticated solutions 16 (Basics)

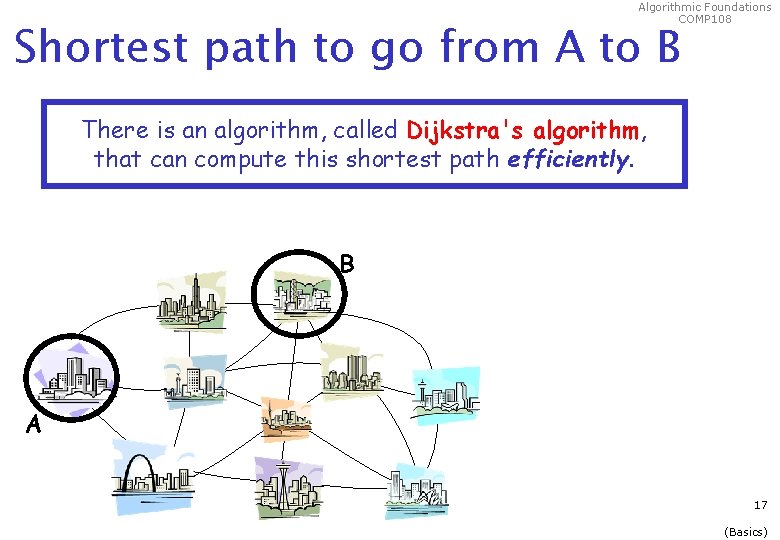
Algorithmic Foundations COMP 108 Shortest path to go from A to B There is an algorithm, called Dijkstra's algorithm, that can compute this shortest path efficiently. B A 17 (Basics)

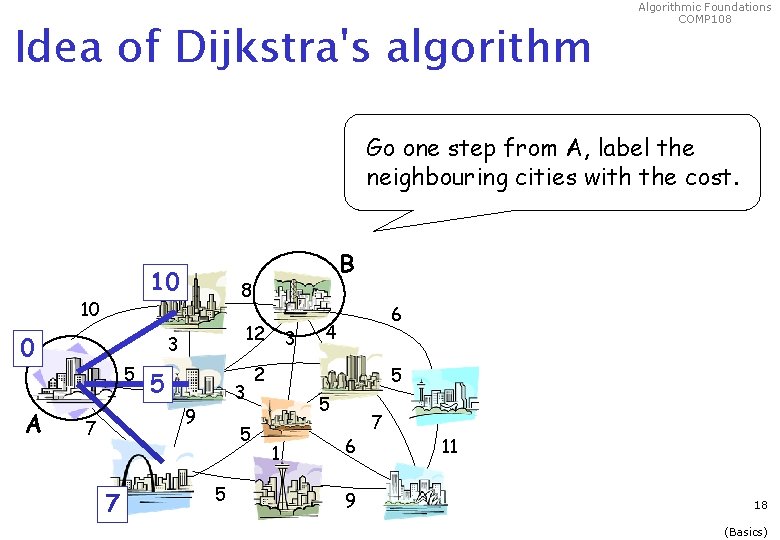
Idea of Dijkstra's algorithm Algorithmic Foundations COMP 108 Go one step from A, label the neighbouring cities with the cost. 10 10 0 A 8 12 3 5 5 3 9 7 7 B 5 5 3 6 4 2 5 5 1 6 9 7 11 18 (Basics)

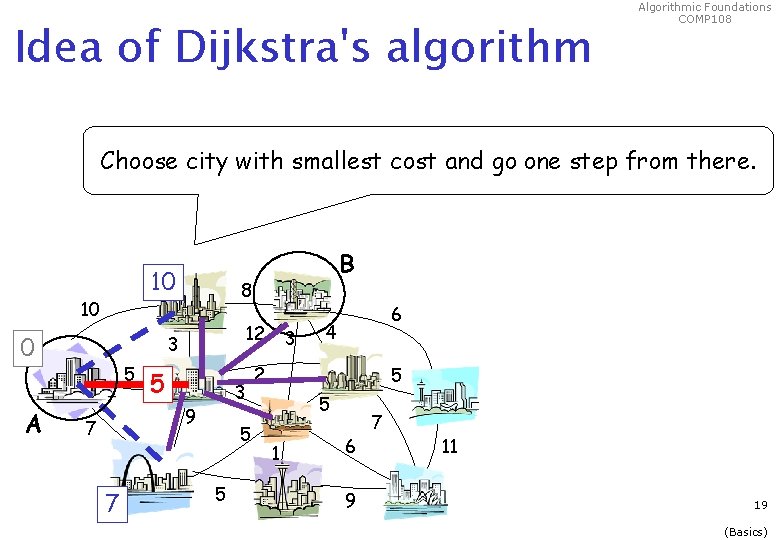
Idea of Dijkstra's algorithm Algorithmic Foundations COMP 108 Choose city with smallest cost and go one step from there. 10 10 0 A 8 12 3 5 5 3 9 7 7 B 5 5 3 6 4 2 5 5 1 6 9 7 11 19 (Basics)

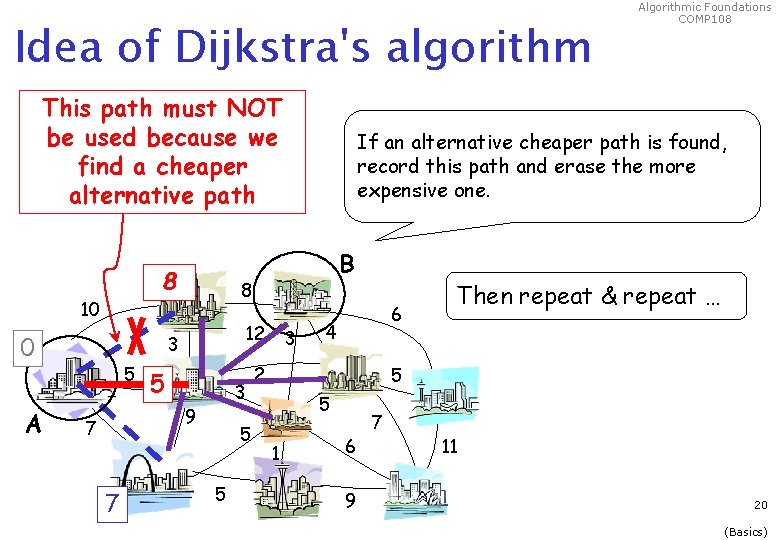
Idea of Dijkstra's algorithm This path must NOT be used because we find a cheaper alternative path 10 8 10 0 A 5 7 B 12 5 3 9 7 If an alternative cheaper path is found, record this path and erase the more expensive one. 8 3 5 5 Algorithmic Foundations COMP 108 3 6 4 2 Then repeat & repeat … 5 5 1 6 9 7 11 20 (Basics)

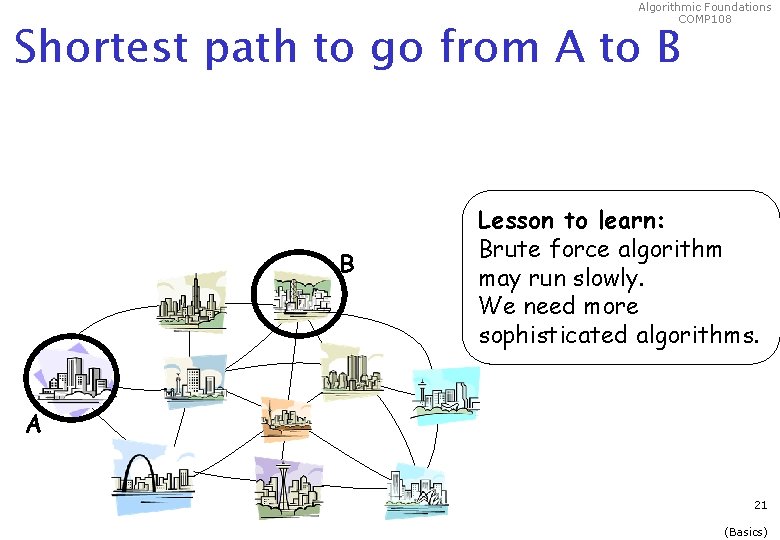
Algorithmic Foundations COMP 108 Shortest path to go from A to B B Lesson to learn: Brute force algorithm may run slowly. We need more sophisticated algorithms. A 21 (Basics)

Algorithmic Foundations COMP 108 How to represent algorithms … ü Able to tell what an algorithm is and have some understanding why we study algorithms Able to use pseudo code to describe algorithm

Algorithm vs Program Algorithmic Foundations COMP 108 An algorithm is a sequence of precise and concise instructions that guide a person/computer to solve a specific problem Algorithms are free from grammatical rules Ø Ø Content is more important than form Acceptable as long as it tells people how to perform a task Programs must follow some syntax rules Ø Ø Form is important Even if the idea is correct, it is still not acceptable if there is syntax error 23 (Basics)

Compute the n-th power Algorithmic Foundations COMP 108 Input: a number x & a non-negative integer n Output: the n-th power of x Algorithm: 1. 2. 3. Set a temporary variable p to 1. Repeat the multiplication p = p * x for n times. Output the result p. 24 (Basics)

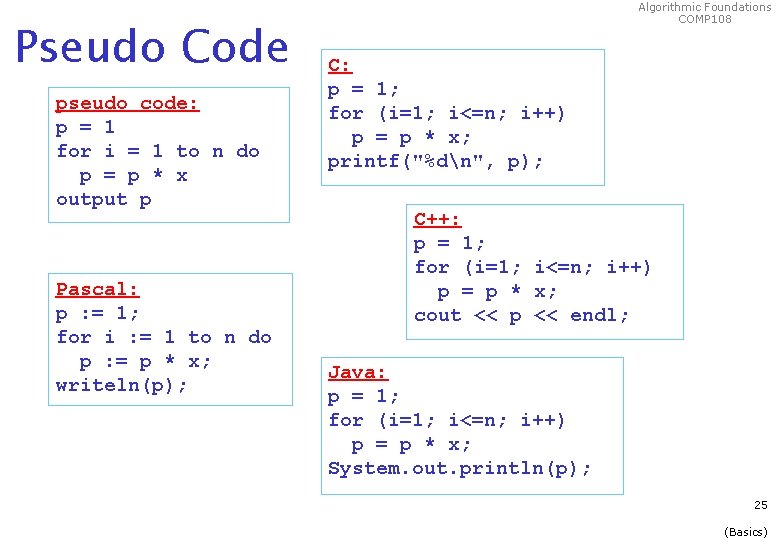
Pseudo Code pseudo code: p = 1 for i = 1 to n do p = p * x output p Pascal: p : = 1; for i : = 1 to n do p : = p * x; writeln(p); Algorithmic Foundations COMP 108 C: p = 1; for (i=1; i<=n; i++) p = p * x; printf("%dn", p); C++: p = 1; for (i=1; i<=n; i++) p = p * x; cout << p << endl; Java: p = 1; for (i=1; i<=n; i++) p = p * x; System. out. println(p); 25 (Basics)

Algorithmic Foundations COMP 108 Pseudo Code Another way to describe algorithm is by pseudo code p = 1 for i = 1 to n do p = p * x output p similar to programming language more like English Combination of both 26 (Basics)

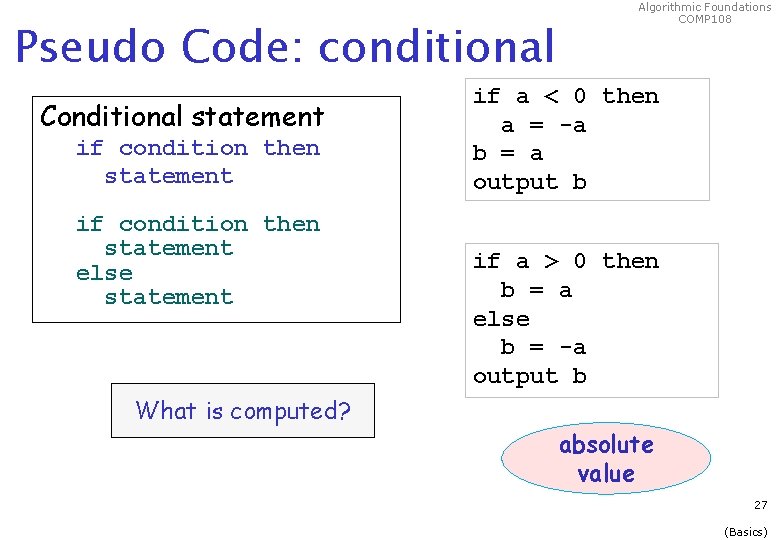
Pseudo Code: conditional Conditional statement if condition then statement else statement Algorithmic Foundations COMP 108 if a < 0 then a = -a b = a output b if a > 0 then b = a else b = -a output b What is computed? absolute value 27 (Basics)

Pseudo Code: iterative (loop) Iterative statement Algorithmic Foundations COMP 108 var automatically increased by 1 after each iteration for var = start_value to end_value do statement while condition do statement condition to CONTINUE the loop 28 (Basics)

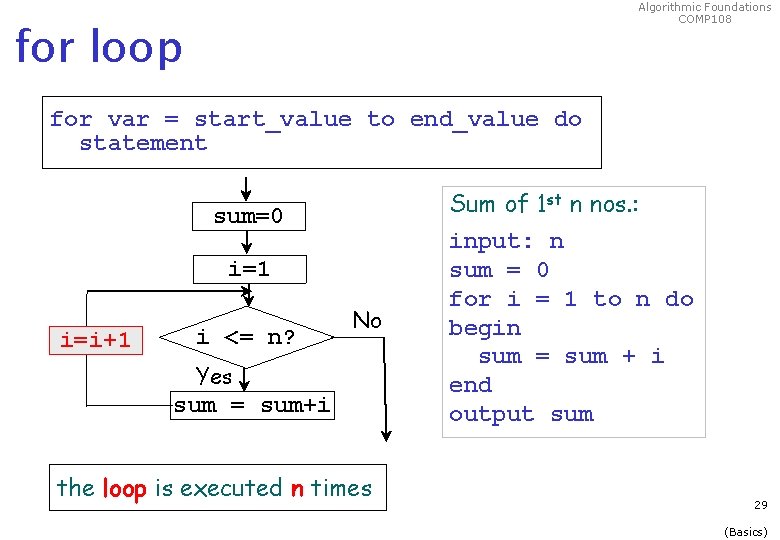
Algorithmic Foundations COMP 108 for loop for var = start_value to end_value do statement sum=0 i=1 i=i+1 i <= n? No Yes sum = sum+i the loop is executed n times Sum of 1 st n nos. : input: n sum = 0 for i = 1 to n do begin sum = sum + i end output sum 29 (Basics)

Algorithmic Foundations COMP 108 for loop for var = start_value to end_value do statement suppose iteration n=4 start 1 2 3 4 end i 1 2 3 4 5 sum 0 1 3 6 10 the loop is executed n times Sum of 1 st n nos. : input: n sum = 0 for i = 1 to n do begin sum = sum + i end output sum trace table 30 (Basics)

Algorithmic Foundations COMP 108 while loop while condition do statement Sum of 1 st n numbers: input: n sum = 0 i = 1 while i <= n do begin sum = sum + i i = i + 1 end output sum condition to CONTINUE the loop Ø Do the same as forloop in previous slides Ø It requires to increment i explicitly 31 (Basics)

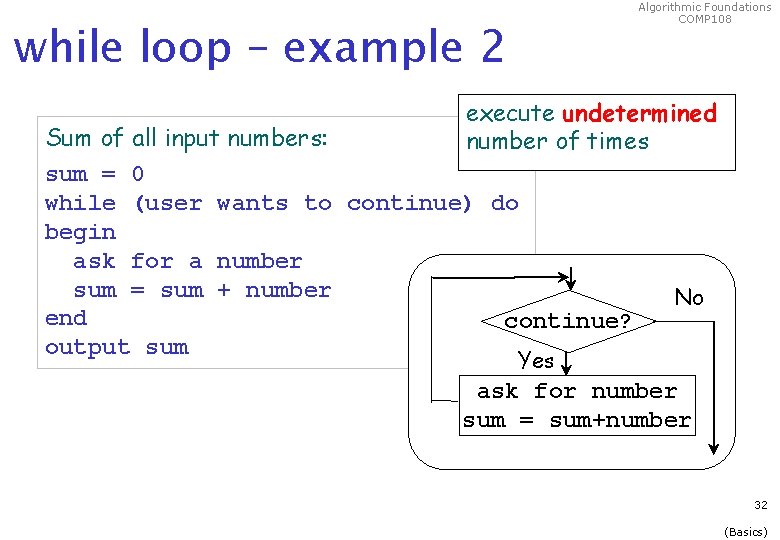
Algorithmic Foundations COMP 108 while loop – example 2 execute undetermined number of times Sum of all input numbers: sum = 0 while (user wants to continue) do begin ask for a number sum = sum + number end continue? output sum No Yes ask for number sum = sum+number 32 (Basics)

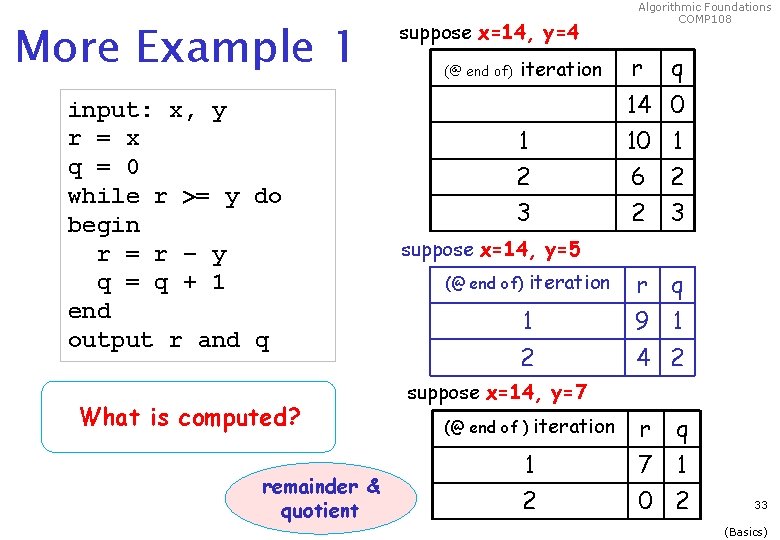
More Example 1 input: x, y r = x q = 0 while r = y do begin r = r − y q = q + 1 end output r and q What is computed? remainder & quotient suppose x=14, y=4 (@ end of) iteration Algorithmic Foundations COMP 108 r q 14 0 1 10 1 2 6 2 3 suppose x=14, y=5 iteration (@ end of) r q 1 9 1 2 4 2 suppose x=14, y=7 (@ end of ) iteration r q 1 7 1 2 0 2 33 (Basics)

More Example 1 - Note input: x, y r = x q = 0 while r = y do begin r = r − y q = q + 1 end output r and q Algorithmic Foundations COMP 108 if condition is r >= ? ? then in the loop we need to decrease r if condition is r <= ? ? then in the loop we need to increase r 34 (Basics)

More Example 2 suppose x=12, y=4 (@ end of ) iteration a%b remainder of a divided b input: x, y i = 1 while i <= y do begin if x%i==0 && y%i==0 then output i i = i+1 end Algorithmic Foundations COMP 108 output (this iteration) i 1 1 1 2 2 2 3 3 4 4 4 5 suppose x=15, y=6 1 1 1 2 What values are output? all common factors 3 2 3 3 4 4 5 5 6 6 7 35 (Basics)

More Example 3 Algorithmic Foundations COMP 108 What value is output? input: x, y Highest Common Factor (HCF) i = y Greatest Common Divisor (GCD) found = false while i >= 1 && !found do begin if x%i==0 && y%i==0 then found = true else i = i-1 Questions: end v what value of found makes output i the loop stop? v when does found change to such value? 36 (Basics)

Algorithmic Foundations COMP 108 Developing pseudo code Write a while-loop to assuming x and y are both integers Find the product of all integers in interval [x, y] Ø Examples x y calculation product 2 5 2 x 3 x 4 x 5 120 10 12 10 x 11 x 12 1320 -4 -2 -4 x -3 x -2 -24 -6 -5 -6 x -5 30 -2 1 -2 x -1 x 0 x 1 0 37 (Basics)

Developing pseudo code Write a while-loop to Algorithmic Foundations COMP 108 assuming x and y are both integers Find the product of all integers in interval [x, y] product = ? ? i = ? ? while ? ? do begin ? ? i = ? ? end output ? ? 38 (Basics)

Algorithmic Foundations COMP 108 Find the product of all integers in interval [x, y] What variables do we need? Øone to store answer, call it product Øone to iterate from x to y, call it i product = ? ? initial value of i? how i changes in loop? Øi start from x; i increase by 1 in loop product = ? ? i = x while ? ? do begin ? ? i = i + 1 end What to do in loop? Ø update product multiply it by i product = product * i Loop condition? Ø continue as long as i is at most y while i <= y initial value of product? Ømultiplication identity product = 1 39 (Basics)

Developing pseudo code Algorithmic Foundations COMP 108 Find the product of all integers in interval [x, y] product = 1 i = x while i <= y do begin product = product * i i = i+1 end output product 40 (Basics)

Algorithmic Foundations COMP 108 Common Mistakes product = 1 i = x while i <= y do begin product = product * i i = i+1 end output product = 0 answer becomes 0 while x <= y do infinite loop because x does not get changed in the loop product * x incorrect! will multiply x for y-x+1 times, i. e. , calculate xyx+1 forget i=i+1 infinite loop because i does not get changed in the loop 41 (Basics)

Pseudo Code: Exercise Algorithmic Foundations COMP 108 Write a while-loop for this: Given two positive integers x and y, list all factors of x which are not factors of y Ø Examples x y factors of x output 6 3 1, 2, 3, 6 2, 6 30 9 1, 2, 3, 5, 6, 10, 15, 30 2, 5, 6, 10, 15, 30 3 6 1, 3 42 (Basics)

Pseudo Code: Exercise Algorithmic Foundations COMP 108 Write a while-loop for this: Given two positive integers x and y, list all factors of x which are not factors of y i = ? ? while ? ? do begin if ? ? then output ? ? i = ? ? end 43 (Basics)

Pseudo Code: Exercise Algorithmic Foundations COMP 108 Write a while-loop for this: Given two positive integers x and y, list all factors of x which are not factors of y Two subproblems: Ø find Ø if all factors of x it is not a factor of y, output it 44 (Basics)

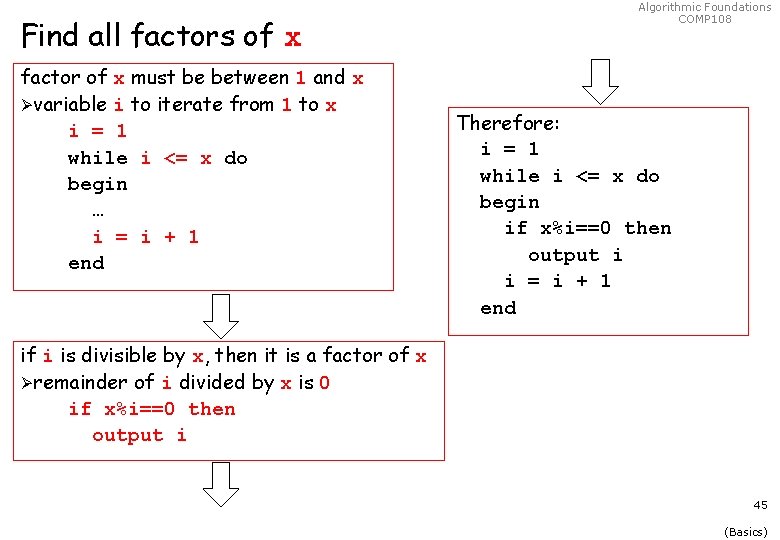
Find all factors of x factor of x must be between 1 and x Øvariable i to iterate from 1 to x i = 1 while i <= x do begin … i = i + 1 end Algorithmic Foundations COMP 108 Therefore: i = 1 while i <= x do begin if x%i==0 then output i i = i + 1 end if i is divisible by x, then it is a factor of x Øremainder of i divided by x is 0 if x%i==0 then output i 45 (Basics)

Algorithmic Foundations COMP 108 1. All factors of x i = 1 while i <= x do begin if x%i==0 then output i i = i + 1 end 3. Finally, i = 1 while i <= x do begin if x%i==0 && y%i!=0 then output i i = i + 1 end 2. Factors of x but not factor of y remainder of i divided by x is 0 Ø remainder of i divided by y is not 0 if x%i==0 && y%i!=0 then output i Ø 46 (Basics)