5 5 Numerical Integration Mt Shasta California Photo


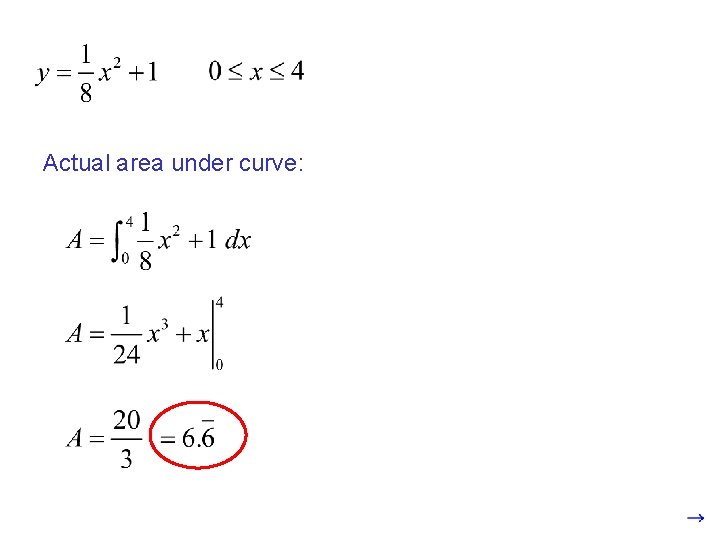






- Slides: 14

5. 5 Numerical Integration Mt. Shasta, California Photo by Vickie Kelly, 1998 Greg Kelly, Hanford High School, Richland, Washington

Using integrals to find area works extremely well as long as we can find the antiderivative of the function. Sometimes, the function is too complicated to find the antiderivative. At other times, we don’t even have a function, but only measurements taken from real life. What we need is an efficient method to estimate area when we can not find the antiderivative.
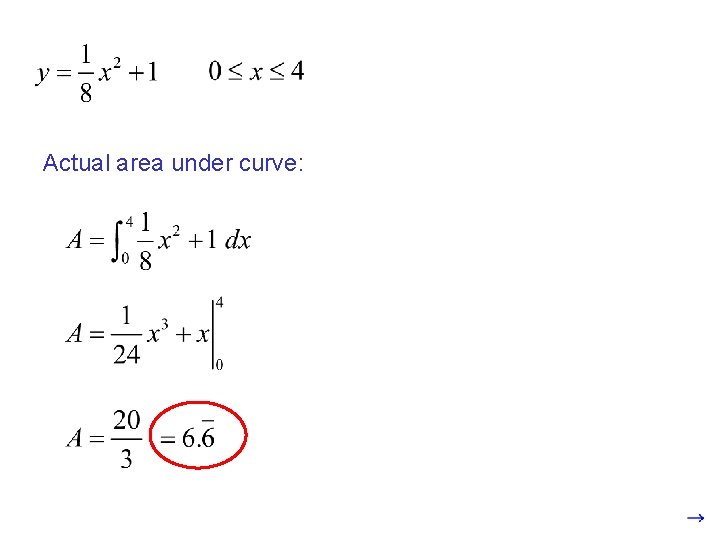
Actual area under curve:

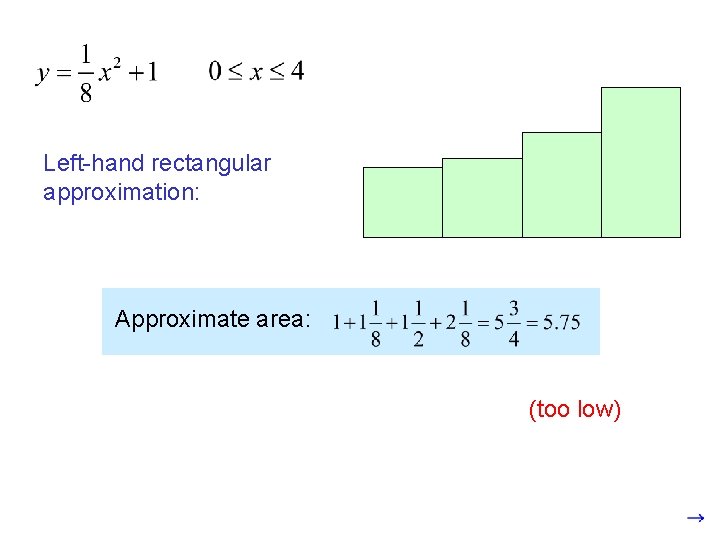
Left-hand rectangular approximation: Approximate area: (too low)

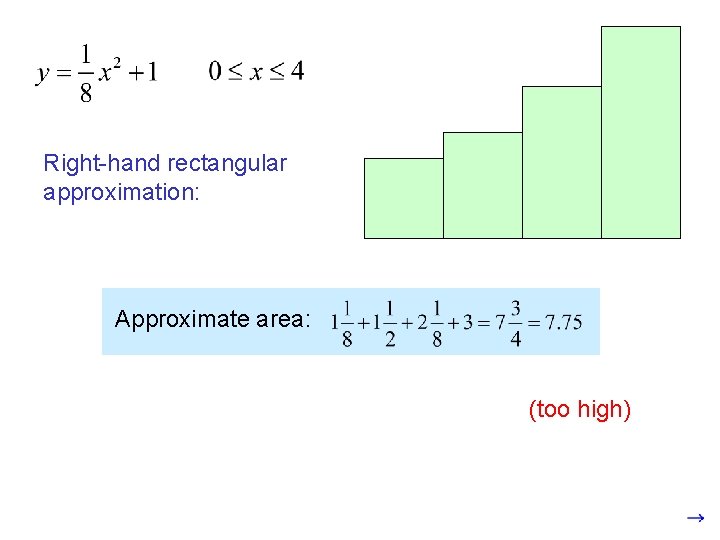
Right-hand rectangular approximation: Approximate area: (too high)

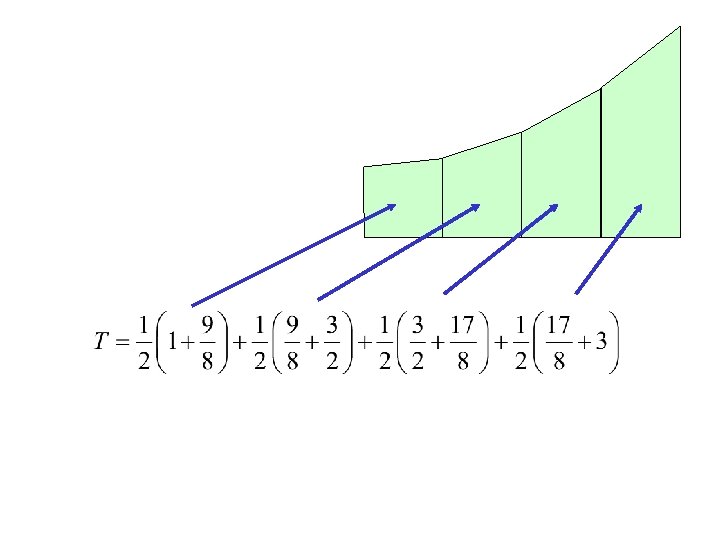
Averaging the two: 1. 25% error (too high)

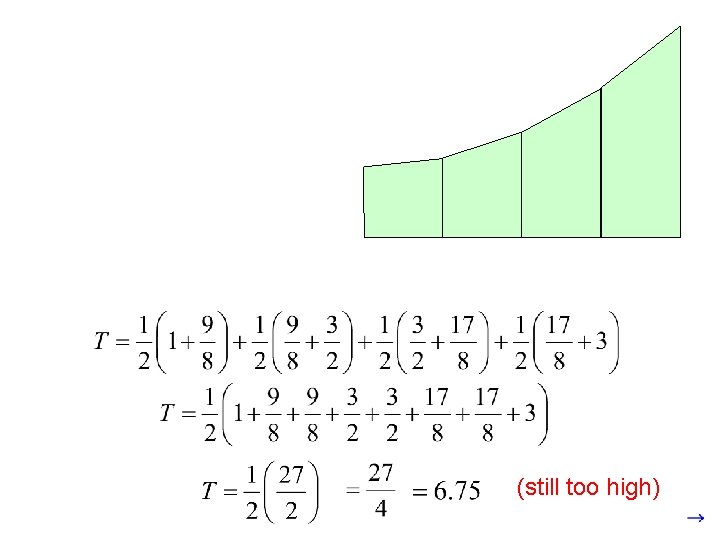
Averaging right and left rectangles gives us trapezoids:

(still too high)

Trapezoidal Rule: ( h = width of subinterval ) This gives us a better approximation than either left or right rectangles.

Compare this with the Midpoint Rule: Approximate area: 0. 625% error (too low) The midpoint rule gives a closer approximation than the trapezoidal rule, but in the opposite direction.

Trapezoidal Rule: 1. 25% error (too high) Midpoint Rule: 0. 625% error (too low) Notice that the trapezoidal rule gives us an answer that has twice as much error as the midpoint rule, but in the opposite direction. If we use a weighted average: Ahhh! This is the exact answer! Oooh! Wow!

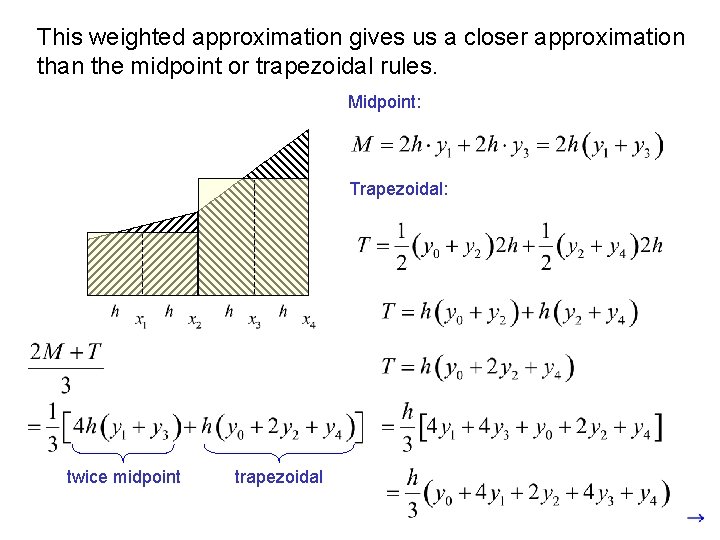
This weighted approximation gives us a closer approximation than the midpoint or trapezoidal rules. Midpoint: Trapezoidal: twice midpoint trapezoidal

Simpson’s Rule: ( h = width of subinterval, n must be even ) Example:

Simpson’s rule can also be interpreted as fitting parabolas to sections of the curve, which is why this example came out exactly. Simpson’s rule will usually give a very good approximation with relatively few subintervals. It is especially useful when we have no equation and the data points are determined experimentally. p
 Shasta regional wound care
Shasta regional wound care Numerical integration c++
Numerical integration c++ Trapezoidal riemann sum
Trapezoidal riemann sum Numerical integration of discrete data
Numerical integration of discrete data Numerical integration
Numerical integration What is numerical integration
What is numerical integration Composite numerical integration
Composite numerical integration Vertical diversification example
Vertical diversification example Example of simultaneous integration
Example of simultaneous integration Forward integration and backward integration
Forward integration and backward integration Linear differential equation formula
Linear differential equation formula Numerical pattern
Numerical pattern Numerical descriptive measures
Numerical descriptive measures Jack box
Jack box Numerical stroop
Numerical stroop