4 6 Matrices 1 Matrices are rectangular arrangements

4. 6 Matrices 1

Matrices are rectangular arrangements of data that are used to represent information in tabular form. a 23 Dimensions: number of rows and columns A is a 2 x 3 matrix Elements of a matrix A are denoted by aij. a 23 = 8 2

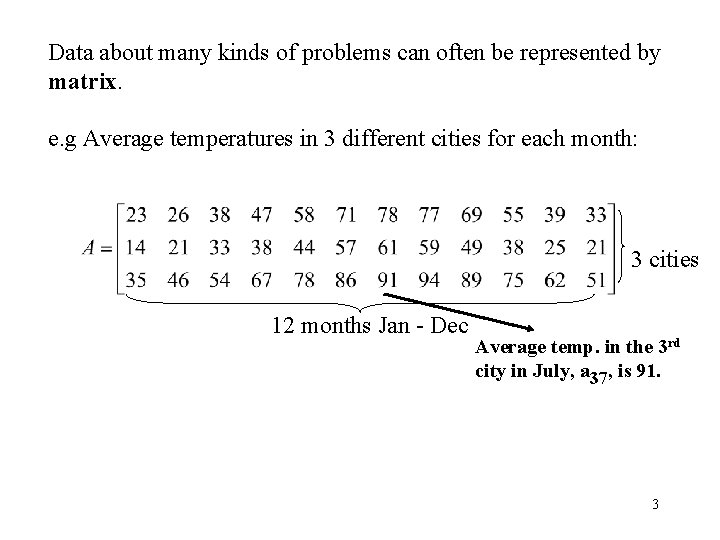
Data about many kinds of problems can often be represented by matrix. e. g Average temperatures in 3 different cities for each month: 3 cities 12 months Jan - Dec Average temp. in the 3 rd city in July, a 37, is 91. 3

Matrix of coefficients Solutions to many problems can be obtained by solving systems of linear equations. For example, the constraints of a problem are represented by the system of linear equations x + y = 70 24 x + 14 y = 1180 is the matrix of coefficient for this system of linear equations. 4

In a matrix, the arrangement of the entries is significant. Therefore, for two matrices to be equal they must have the same dimensions and the same entries in each location. Example: Let If X = Y, then x = 3, y = 6, z = 2, and w = 0. 5

Square Matrix is a matrix in which the number of rows equals the number of columns. • Main Diagonal: in a n x n square matrix, the elements a 11, a 22, a 33, …, ann form the main diagonal of the matrix. • Symmetric matrix: If the corresponding elements match when we think of folding the matrix along the main diagonal, then the matrix is symmetric about the main diagonal. In a symmetric matrix, aij = aji. 6

Example: The square matrix Main Diagonal is symmetric. Note that a 21 = a 12 = 5 a 31 = a 13 = 7 a 32 = a 23 = 2 7

Matrix Operations 1. Scalar multiplication: 2. Multiply each entry of a matrix by a fixed single number called scalar. 3. ex: The result of multiplying matrix 4. by the scalar r = 3 is 8

2. Addition: 3. Adding the corresponding elements of 2 matrices that have the same dimensions. 4. ex: For 5. the matrix A+B is 9

3. Subtraction: 4. defined by A – B = A + (-1)B. 5. 6. 7. In a zero matrix, all entries are 0. An n m zero matrix is denoted by 0. If A and B are n x m matrices and r and s are scalars, the following matrix equations are true: 8. 0+A=A 9. A+B=B+A 10. (A + B) + C = A + (B + C) 11. r(A + B) = r. A + r. B 12. (r + s)A = r. A + s. A 13. r(s. A) = (rs)A 10

4. Multiplication of matrices: 5. 6. 7. 8. 9. 10. 11. A: B: n m matrix The result C is an n p matrix. m p matrix A B = C, where An entry in row i, column j of A B is obtained by multiplying elements in row i of A by the corresponding elements in column j of B and adding the results. To compute A times B, the number of columns in A must equal the number of rows in B. 11

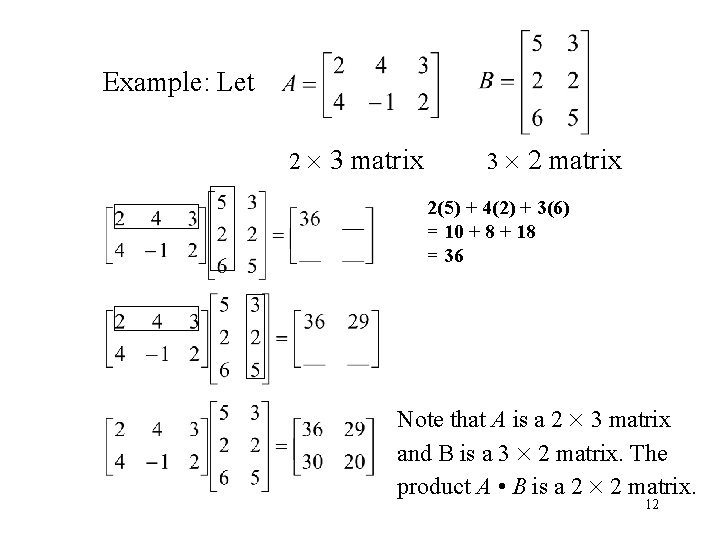
Example: Let 2 3 matrix 3 2 matrix 2(5) + 4(2) + 3(6) = 10 + 8 + 18 = 36 Note that A is a 2 3 matrix and B is a 3 2 matrix. The product A • B is a 2 2 matrix. 12

Example: Compute A B and B A for Note: A B B A. 13

Where A, B and C are matrices of appropriate dimensions and r and s are scalars, the following matrix equations are true: (The notation A(B C) is shorthand for A (B C) ) A(B C) = (A B)C A(B + C) = A B + A C (A + B)C = A C + B C r. A s. B = (rs)(A B) 14

Identity matrix The n n matrix with 1 s along the main diagonal and 0 s elsewhere is called the identity matrix, denoted by I. If we multiply I times any n n matrix A, we get A as the result. The equation I • A=A • I=A holds. Let Similarly, A • I=A. 15

An n n matrix A is invertible if there exists an n n matrix B such that A • B=B • A=I In this case B is called the inverse of A, denoted by A-1. Let Then, following the rules of matrix multiplication, it can be shown that A • B = B • A = I, so B = A-1. 16

Boolean Matrices with only 0 s and 1 s as entries are called Boolean matrices. Boolean multiplication: x y = min(x, y) Boolean addition: x y = max(x, y) Boolean matrix multiplication A B is defined by m Cij = (aik bkj) k=1 A B: corresponding elements are combined using Boolean multiplication. A B: corresponding elements are combined using Boolean addition. 17

Let A and B be Boolean matrices, Then And the Boolean product A B is 18