3 2 Graph Traversal Connected Component Connected component

3. 2 Graph Traversal

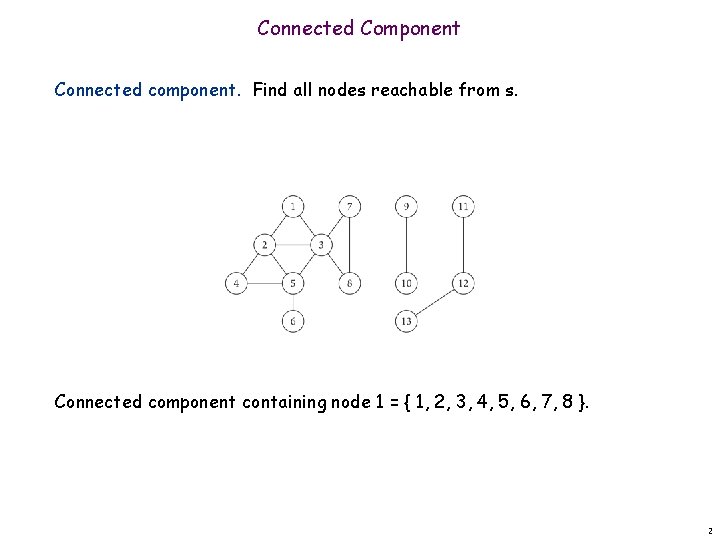
Connected Component Connected component. Find all nodes reachable from s. Connected component containing node 1 = { 1, 2, 3, 4, 5, 6, 7, 8 }. 2

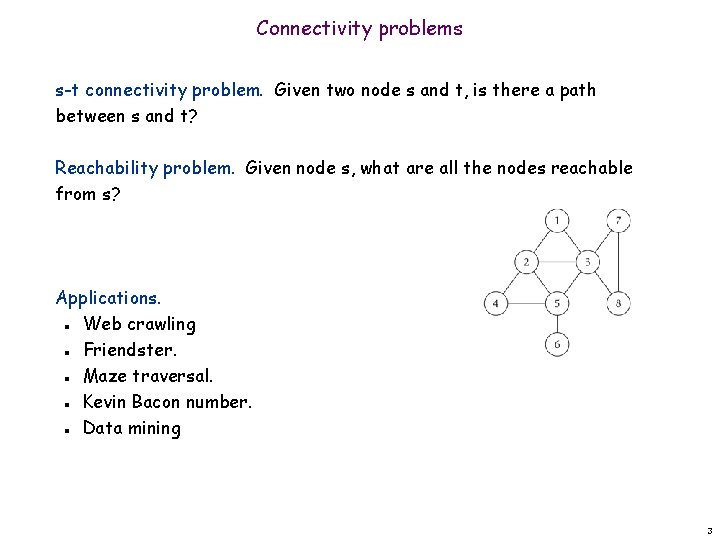
Connectivity problems s-t connectivity problem. Given two node s and t, is there a path between s and t? Reachability problem. Given node s, what are all the nodes reachable from s? Applications. Web crawling Friendster. Maze traversal. Kevin Bacon number. Data mining n n n 3

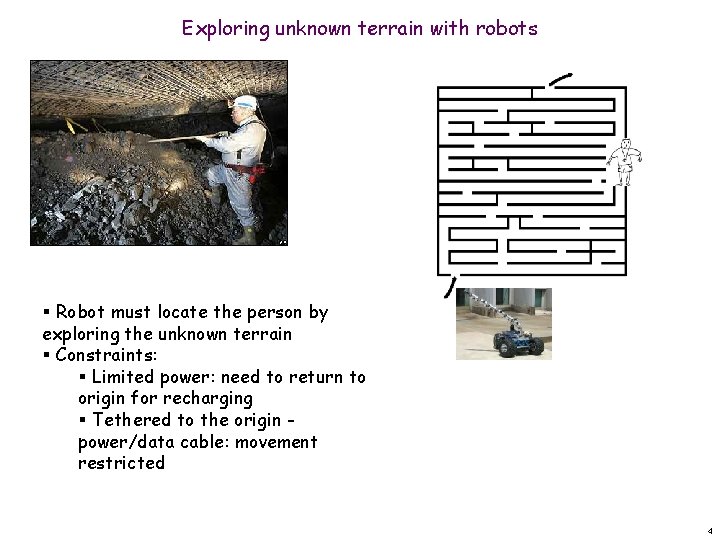
Exploring unknown terrain with robots § Robot must locate the person by exploring the unknown terrain § Constraints: § Limited power: need to return to origin for recharging § Tethered to the origin power/data cable: movement restricted 4

Generic Connected Components Algorithm Connected component. Find all nodes reachable from s. R w s P u v Theorem. Upon termination, R is the connected component containing s. Proof. By construction, each node in R has a path from s. Suppose there is a node w R that has a path P in G from s. n s R, and w R there is a first node v P, v s n Immediate predecessor u of v on P must be in R n So there is edge (u, v), with u R and v R n Therefore, v should have been added to R 5

Finding all Connected Components While there is an unvisited node s: Compute the connected component containing s Mark all nodes in this component as visited n n 6

Generic Connected Components Algorithm n Path from s to any node t can be recovered For every node v, record edge (u, v) that was considered when v was added Trace edges backwards from t Gives a “search tree” n n Choice of edge to grow R is unspecified. Two possible ways: Breadth First Search Depth First Search n n 7

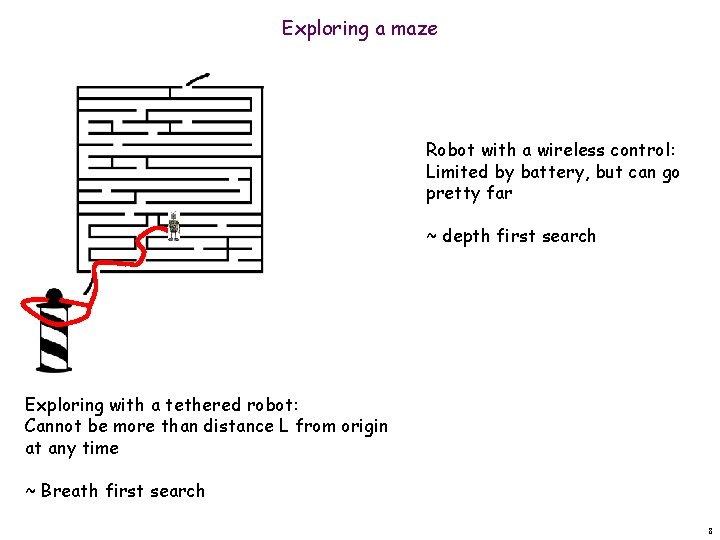
Exploring a maze Robot with a wireless control: Limited by battery, but can go pretty far ~ depth first search Exploring with a tethered robot: Cannot be more than distance L from origin at any time ~ Breath first search 8

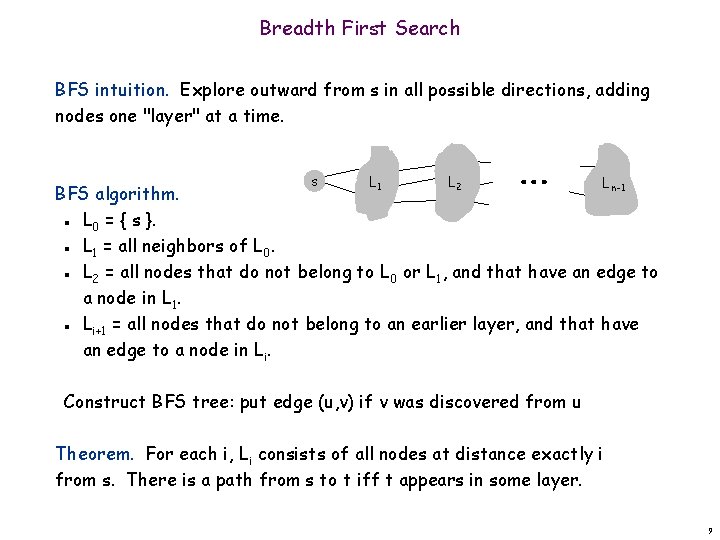
Breadth First Search BFS intuition. Explore outward from s in all possible directions, adding nodes one "layer" at a time. s L 1 L 2 L n-1 BFS algorithm. L 0 = { s }. L 1 = all neighbors of L 0. L 2 = all nodes that do not belong to L 0 or L 1, and that have an edge to a node in L 1. Li+1 = all nodes that do not belong to an earlier layer, and that have an edge to a node in Li. n n Construct BFS tree: put edge (u, v) if v was discovered from u Theorem. For each i, Li consists of all nodes at distance exactly i from s. There is a path from s to t iff t appears in some layer. 9

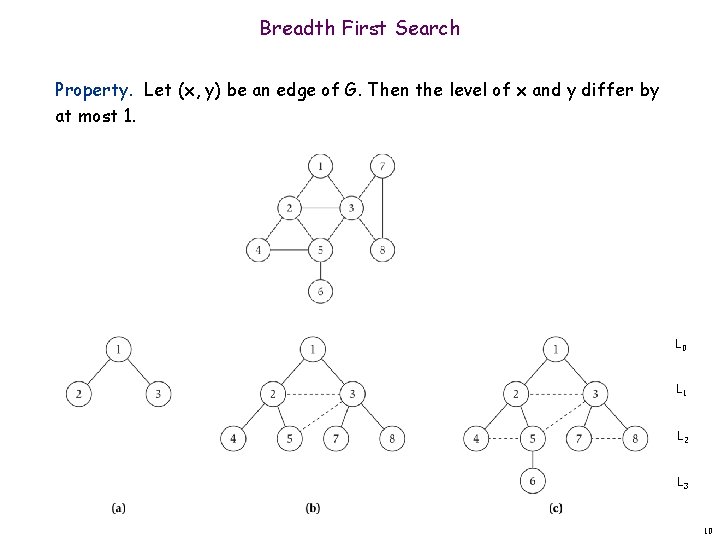
Breadth First Search Property. Let (x, y) be an edge of G. Then the level of x and y differ by at most 1. L 0 L 1 L 2 L 3 10

Depth First Search DFS intuition. Follow the first unexplored edge out of each node, and backtrack when a “dead end” is reached - a node that has no more unexplored edges out of it. Searching a Maze: Right-Hand Rule. Rooms are nodes and passages are edges Always follow the first passage on the right n n 11

DFS Algorithm Constructing a DFS Tree • Make s the root • Make u the parent of v if u is responsible for the discovery of v 12

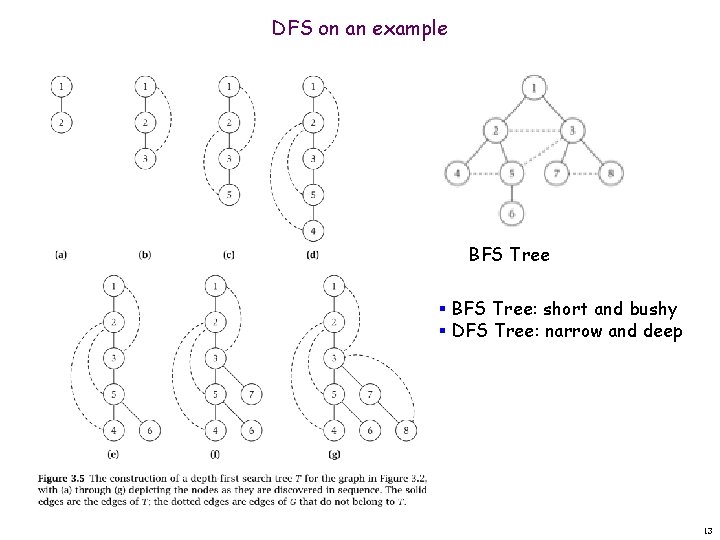
DFS on an example BFS Tree § BFS Tree: short and bushy § DFS Tree: narrow and deep 13

Properties of DFS trees For a recursive call DFS(u), all nodes that are marked “Explored” during this call are descendants of u Theorem. Let T be a DFS tree. Let x and y be nodes in T and let (x, y) be an edge of G that is not in T. Then one of x or y is an ancestor of the other Proof. Suppose x was explored before y. When (x, y) was examined, it was not added to T because y was marked “Explored” Therefore, y must be a descendant of x. 14

Implementing Graph Traversal using Queues and Stacks Section 3. 3 [KT] 15

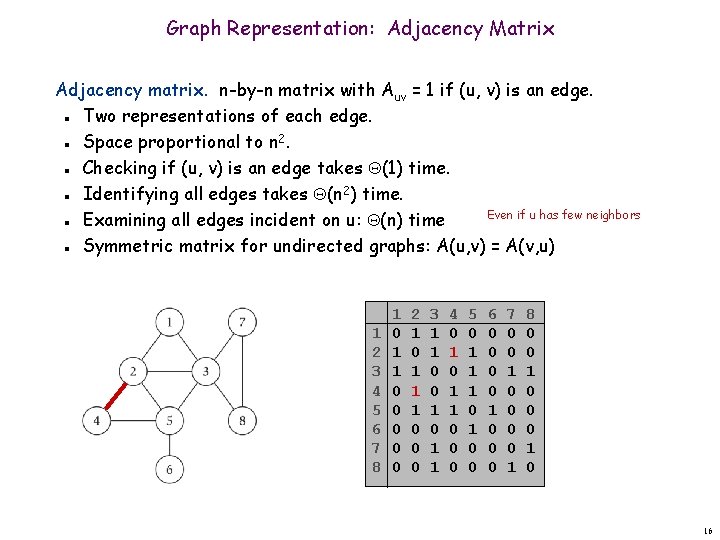
Graph Representation: Adjacency Matrix Adjacency matrix. n-by-n matrix with Auv = 1 if (u, v) is an edge. Two representations of each edge. Space proportional to n 2. Checking if (u, v) is an edge takes (1) time. Identifying all edges takes (n 2) time. Even if u has few neighbors Examining all edges incident on u: (n) time Symmetric matrix for undirected graphs: A(u, v) = A(v, u) n n n 1 2 3 4 5 6 7 8 1 0 1 1 0 0 0 2 1 0 1 1 1 0 0 0 3 1 1 0 0 1 1 4 0 1 1 0 0 0 5 0 1 1 1 0 0 6 0 0 1 0 0 0 7 0 0 1 8 0 0 1 0 16

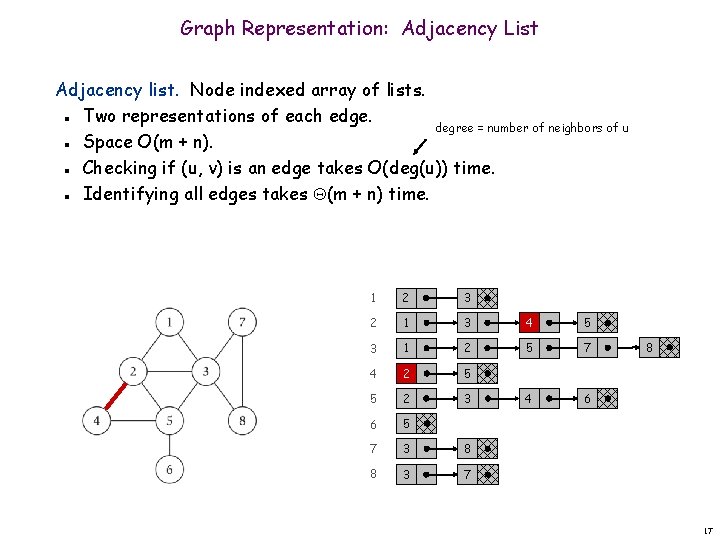
Graph Representation: Adjacency List Adjacency list. Node indexed array of lists. Two representations of each edge. degree = number of neighbors of u Space O(m + n). Checking if (u, v) is an edge takes O(deg(u)) time. Identifying all edges takes (m + n) time. n n 1 2 3 2 1 3 4 5 3 1 2 5 7 4 2 5 5 2 3 4 6 6 5 7 3 8 8 3 7 8 17

The Best Representation for Searching requires exploring all the edges incident on a node n O(deg(v)) time for Adjacency List, instead of (n) time for Adjacency Matrix n Adjacency List more suitable for Searching algorithms n Need another data structure for storing nodes that are currently being explored n 18

Queues and Stacks Queues. n Elements extracted in first-in, first-out (FIFO) order n Can be implemented by a linked list Stacks. n Elements extracted in last-in, first-out (LIFO) order n Can be implemented by a doubly linked list or an array 19

Implementing Breadth-First Search Algorithm can be run with a single list L, implemented as a queue, instead of separate lists L[i] 20

Breadth First Search: Analysis Theorem. The above implementation of BFS runs in O(m + n) time if the graph is given by its adjacency representation. Pf. n n Easy to prove O(n 2) running time: – at most n lists L[i] – each node occurs on at most one list; for loop runs n times – when we consider node u, there are n incident edges (u, v), and we spend O(1) processing each edge Actually runs in O(m + n) time: – when we consider node u, there are deg(u) incident edges (u, v) – total time processing edges is u V deg(u) = 2 m ▪ each edge (u, v) is counted exactly twice in sum: once in deg(u) and once in deg(v) 21

Implementing Depth-First Search Order of insertion into S depends on Adjacency List Different Adjacency List orders can give different traversals 22

Constructing a DFS Tree If Explored[v] = false Parent[v] = u DFS Tree formed by taking all edges (u, parent[u]) for All u ≠s 23

Running Time of DFS Implementation using Stacks n n n Main step: add/delete node in Stack: O(1) per operation How many such operations? deg(v) = degree of node v Node v is added to S each time one of its neighbors is explored Total number of nodes added to S ≤ ∑v deg(v)v = 2 m The above implementation of DFS runs in time O(n+m), if the graph is given by an adjacency list representation. n 24

3. 5 Connectivity in Directed Graphs

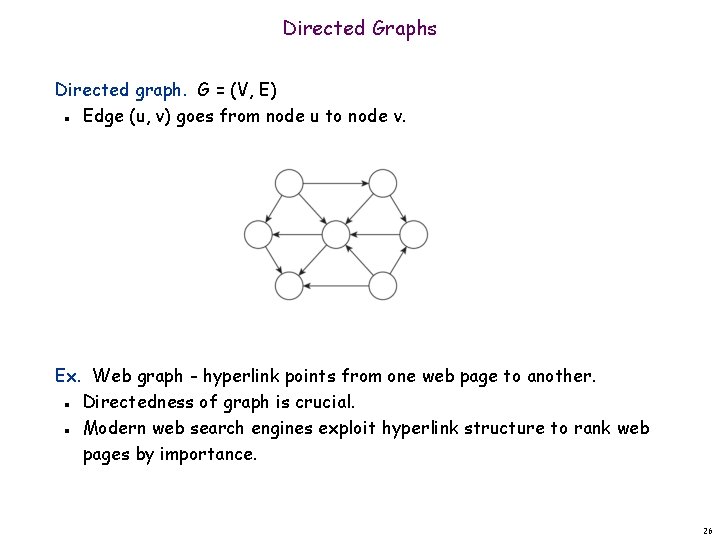
Directed Graphs Directed graph. G = (V, E) Edge (u, v) goes from node u to node v. n Ex. Web graph - hyperlink points from one web page to another. Directedness of graph is crucial. Modern web search engines exploit hyperlink structure to rank web pages by importance. n n 26

Graph Search Directed reachability. Given a node s, find all nodes reachable from s. Directed s-t shortest path problem. Given two node s and t, what is the length of the shortest path between s and t? Graph search. BFS, DFS extend naturally to directed graphs. Web crawler. Start from web page s. Find all web pages linked from s, either directly or indirectly. 27

Strong Connectivity Def. Node u and v are mutually reachable if there is a path from u to v and also a path from v to u. Def. A graph is strongly connected if every pair of nodes is mutually reachable. Lemma. Let s be any node. G is strongly connected iff every node is reachable from s, and s is reachable from every node. Pf. Follows from definition. Pf. Path from u to v: concatenate u-s path with s-v path. Path from v to u: concatenate v-s path with s-u path. ▪ ok if paths overlap s u v 28

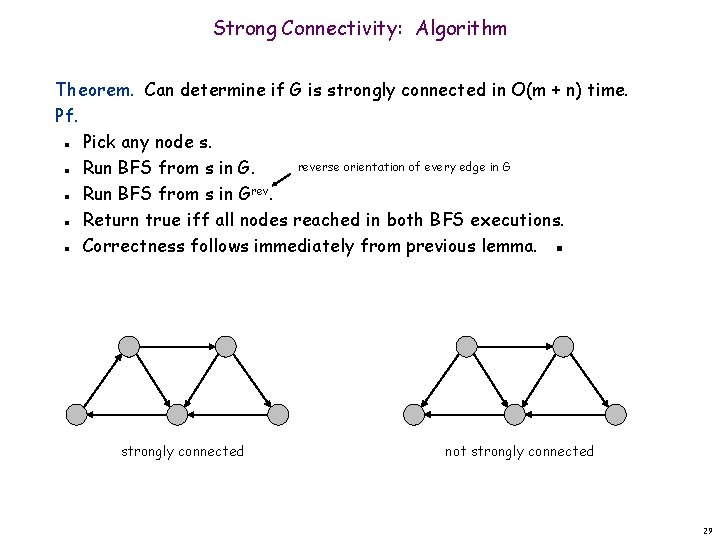
Strong Connectivity: Algorithm Theorem. Can determine if G is strongly connected in O(m + n) time. Pf. Pick any node s. reverse orientation of every edge in G Run BFS from s in Grev. Return true iff all nodes reached in both BFS executions. Correctness follows immediately from previous lemma. ▪ n n n strongly connected not strongly connected 29