Algebra 1 Topic 2 Table of Contents Recommended

Algebra 1 Topic 2

Table of Contents • Recommended Instructional Design and Planning Continuum ……. Slide 3 • Vocabulary …………………………… Slides 4 – 17 • Pre-Requisite Practice Items ……………………… Slides 18 – 39 • Reporting Category Practice Items ………………… Slides 40 – 72

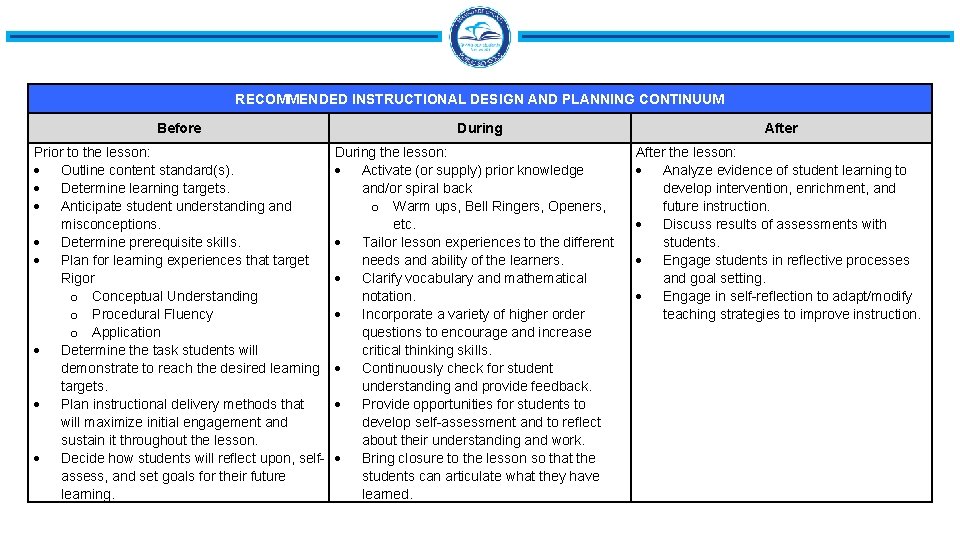
RECOMMENDED INSTRUCTIONAL DESIGN AND PLANNING CONTINUUM Before Prior to the lesson: Outline content standard(s). Determine learning targets. Anticipate student understanding and misconceptions. Determine prerequisite skills. Plan for learning experiences that target Rigor o Conceptual Understanding o Procedural Fluency o Application Determine the task students will demonstrate to reach the desired learning targets. Plan instructional delivery methods that will maximize initial engagement and sustain it throughout the lesson. Decide how students will reflect upon, selfassess, and set goals for their future learning. During the lesson: Activate (or supply) prior knowledge and/or spiral back o Warm ups, Bell Ringers, Openers, etc. Tailor lesson experiences to the different needs and ability of the learners. Clarify vocabulary and mathematical notation. Incorporate a variety of higher order questions to encourage and increase critical thinking skills. Continuously check for student understanding and provide feedback. Provide opportunities for students to develop self-assessment and to reflect about their understanding and work. Bring closure to the lesson so that the students can articulate what they have learned. After the lesson: Analyze evidence of student learning to develop intervention, enrichment, and future instruction. Discuss results of assessments with students. Engage students in reflective processes and goal setting. Engage in self-reflection to adapt/modify teaching strategies to improve instruction.

Vocabulary

Mathematically Speaking! Choose 3 -4 vocabulary words for the day. Throughout the lesson, as students respond to your questions or are presenting a problem on the board, mark a tally when a vocabulary word is used accurately. This can be turned into a competition among groups or between periods. Examples of accuracy • translation vs slide • variable vs letter • addition property of equality vs adding on both sides

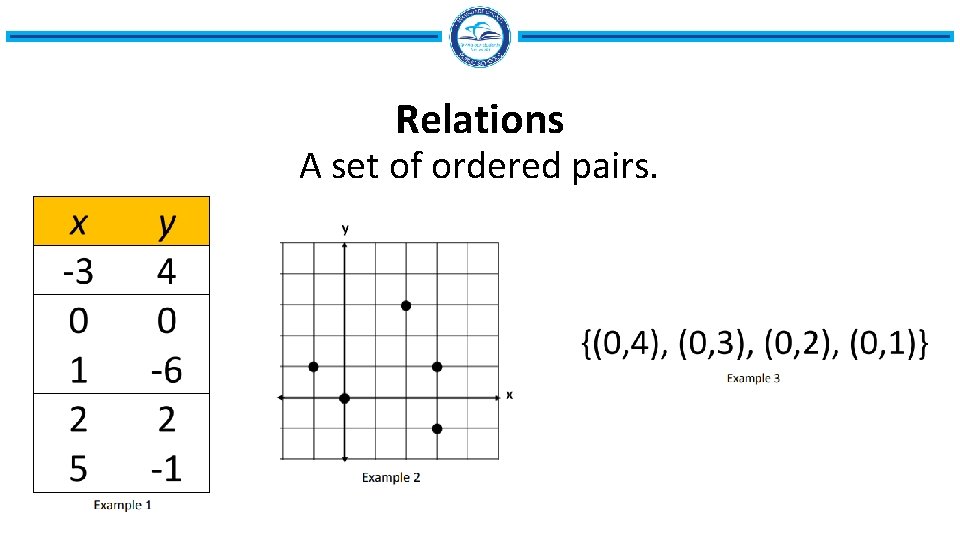
Relations A set of ordered pairs.

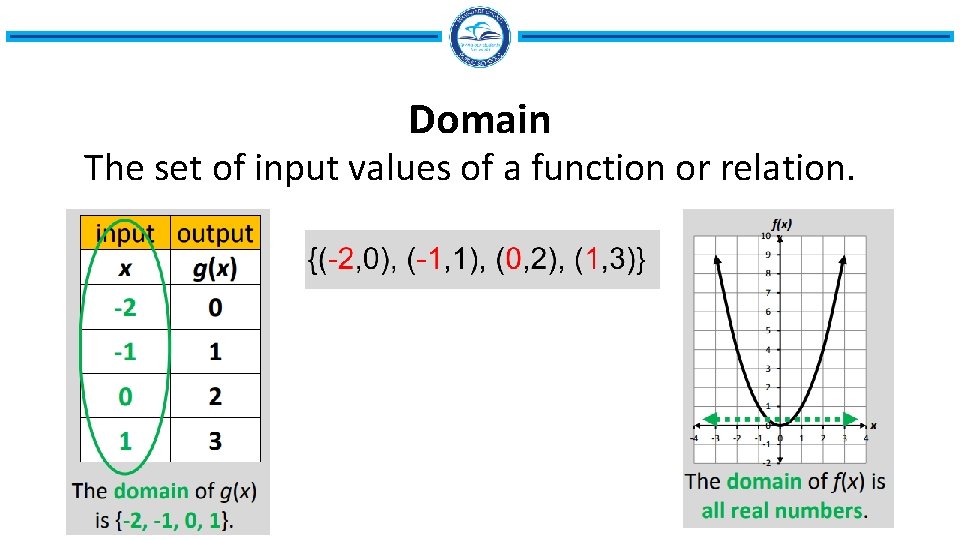
Domain The set of input values of a function or relation.

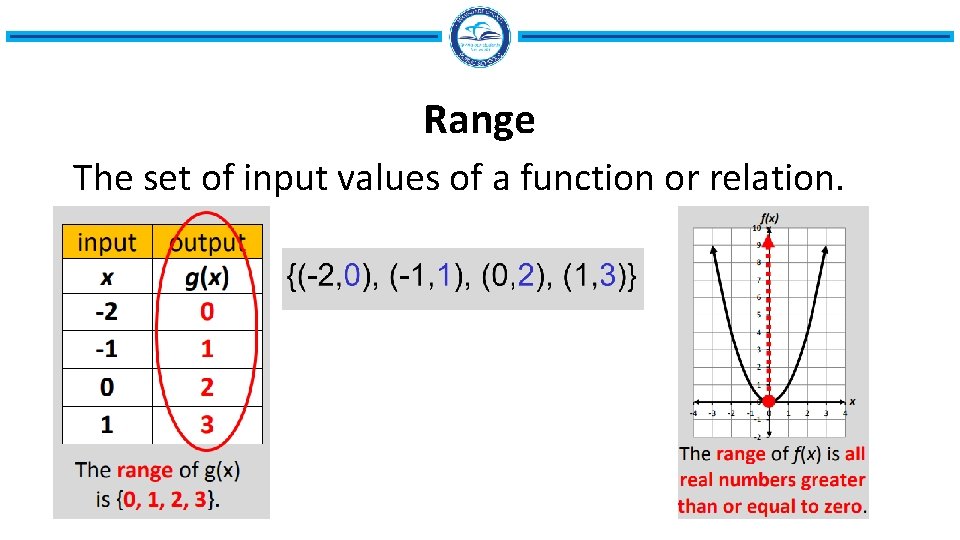
Range The set of input values of a function or relation.

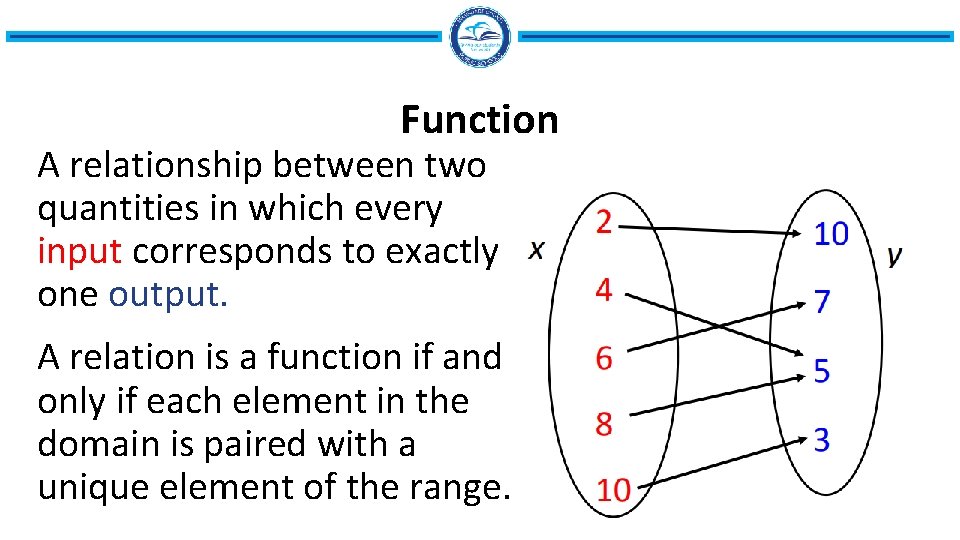
Function A relationship between two quantities in which every input corresponds to exactly one output. A relation is a function if and only if each element in the domain is paired with a unique element of the range.

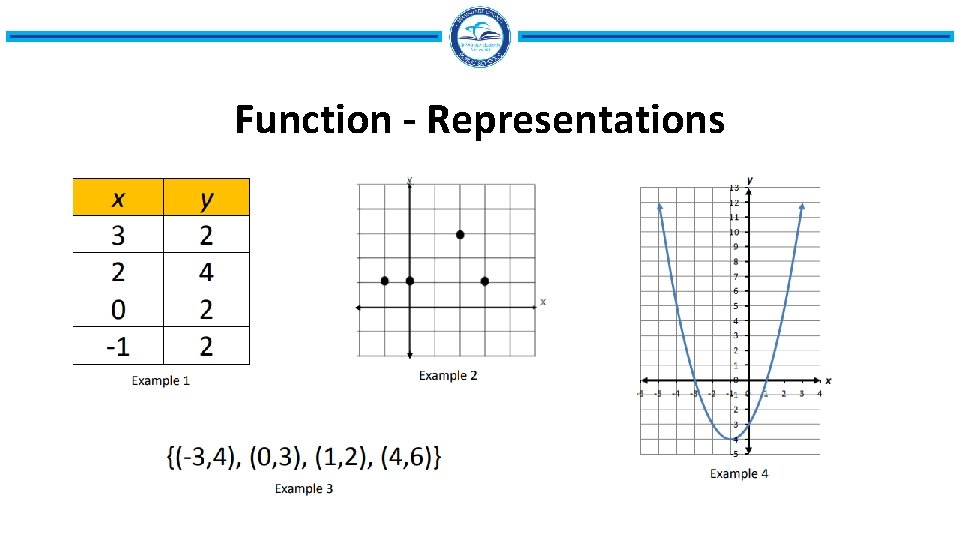
Function - Representations

Function Rule An algebraic expression that defines a function. •

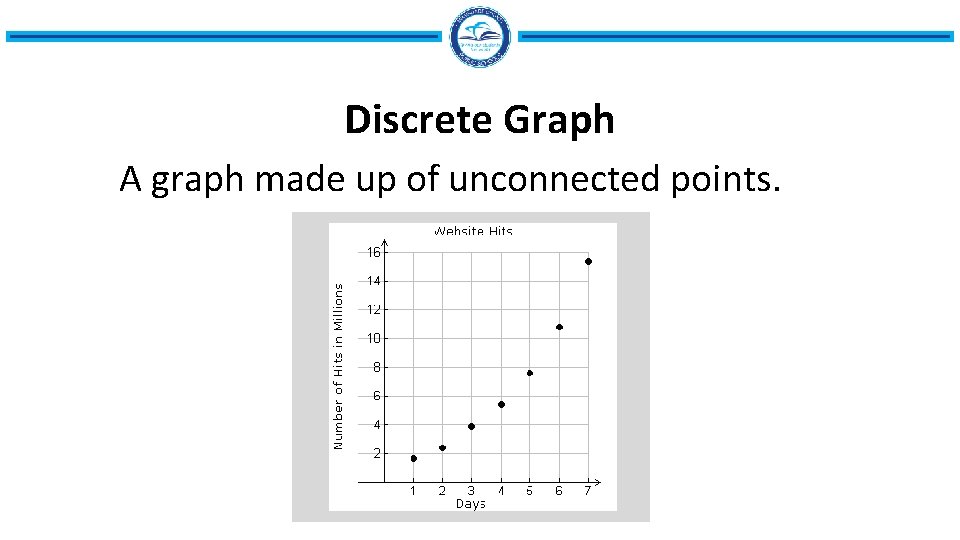
Discrete Graph A graph made up of unconnected points.

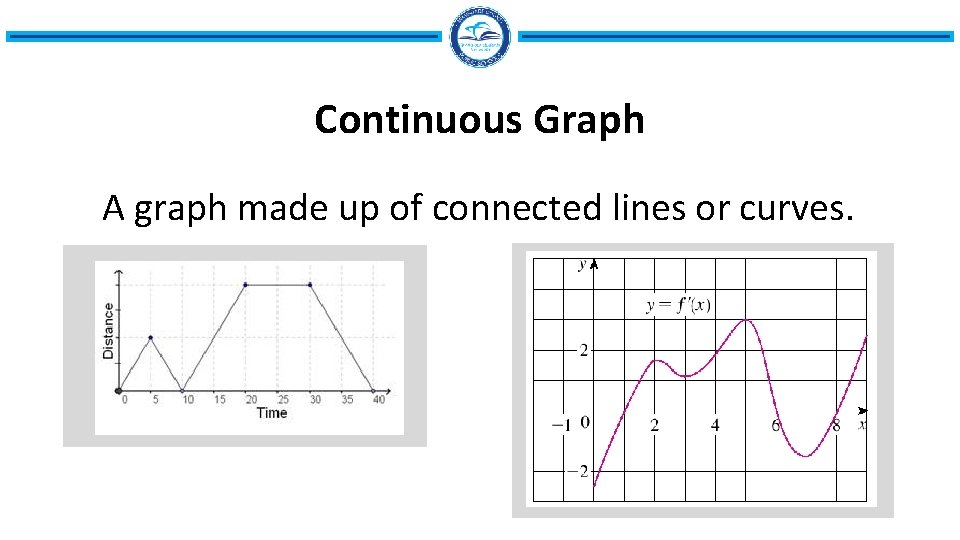
Continuous Graph A graph made up of connected lines or curves.

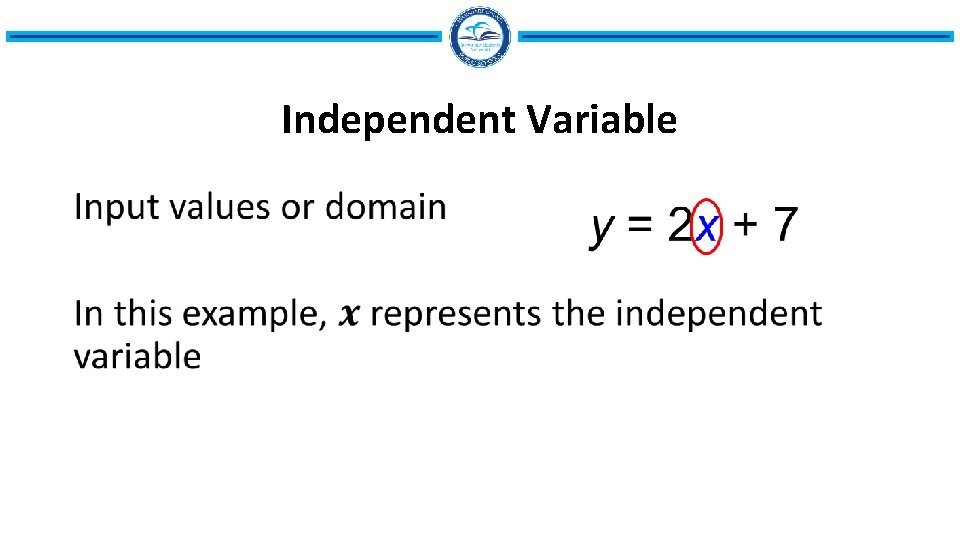
Independent Variable •

Dependent Variable •

Dependent and Independent Variable Determine the distance a car will travel going 55 mph.

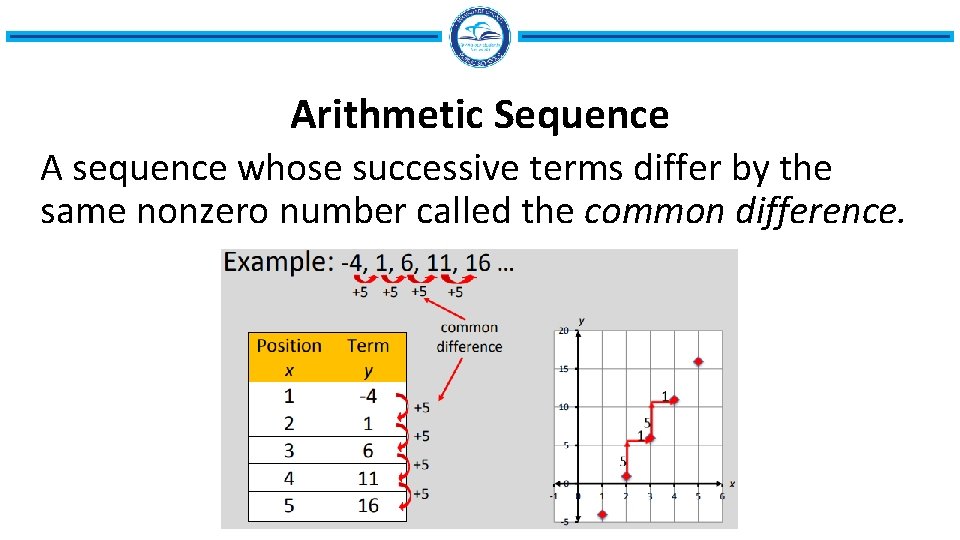
Arithmetic Sequence A sequence whose successive terms differ by the same nonzero number called the common difference.

Operations on Functions Operations on functions are similar to operations on numbers. Each operation has a formal definition which produces a new function.

• Composition of Functions

Pre-Requisite Practice Items

Pre-Requisites MAFS. 8. F. 1. 1 Identifying Algebraic Functions

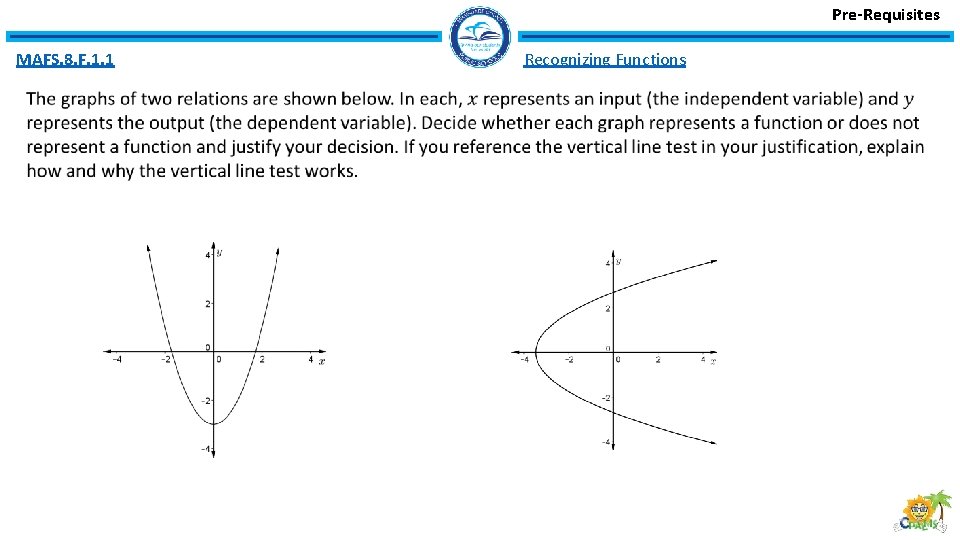
Pre-Requisites MAFS. 8. F. 1. 1 Recognizing Functions

Pre-Requisites MAFS. 8. F. 1. 1 Tabulating Functions 4 12 3 – 2 – 1 – 3 1 – 1. 8 0 – 4 5 – 2. 2 – 5 – 21 – 4 3 1 – 3 – 2 0 4 12 1 1. 8 – 2 0 – 6 3. 8

Pre-Requisites MAFS. 8. F. 1. 1 What Is a Function? Define the term function as completely and precisely as you can.

Pre-Requisites MAFS. 8. F. 1. 1 The Customers A certain business keeps a database of information about its customers.

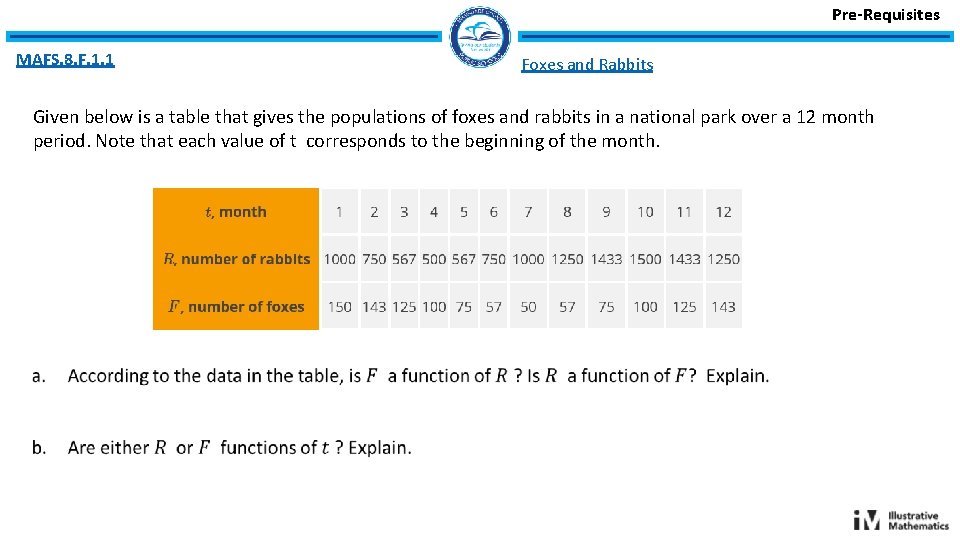
Pre-Requisites MAFS. 8. F. 1. 1 Foxes and Rabbits Given below is a table that gives the populations of foxes and rabbits in a national park over a 12 month period. Note that each value of t corresponds to the beginning of the month.

Pre-Requisites MAFS. 8. F. 1. 1 US Garbage, Version 1 The following table shows the amount of garbage that was produced in the US each year between 2002 and 2010 (as reported by the EPA). a. How much garbage was produced in 2004? b. In which year did the US produce 251 million tons of garbage? c. Does the table describe a linear function? d. Draw a graph that shows this data.

Pre-Requisites MAFS. 8. F. 1. 1 Pennies to Heaven a. In 2011 there were approximately 5 billion pennies minted. If all of these pennies were placed in a single stack, how many miles high would that stack be? b. In the past 100 years, nearly 500 billion pennies have been minted. If all of these pennies were placed in a single stack, how many miles high would that stack be? c. The distance from the moon to the earth is about 239, 000 miles. How many pennies would need to be in a stack in order to reach the moon?

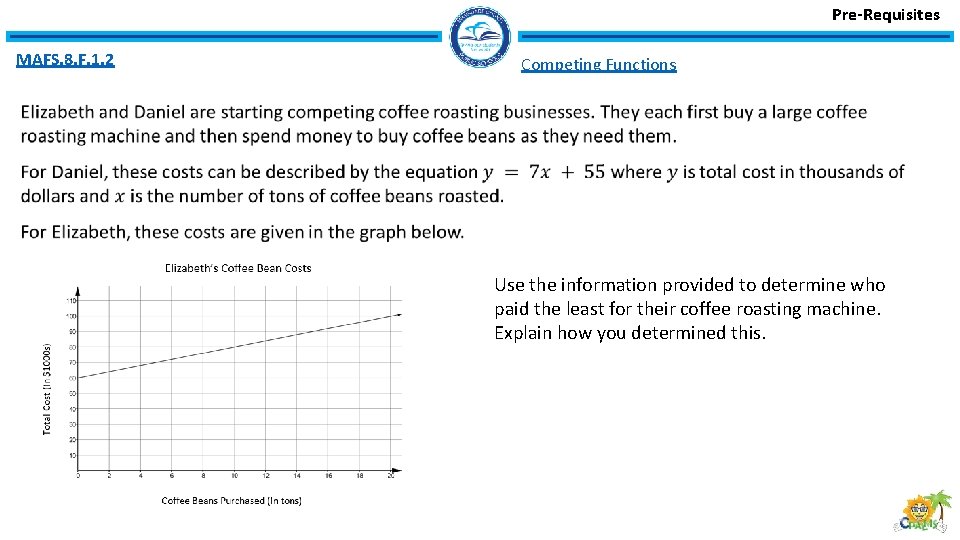
Pre-Requisites MAFS. 8. F. 1. 2 Competing Functions Use the information provided to determine who paid the least for their coffee roasting machine. Explain how you determined this.

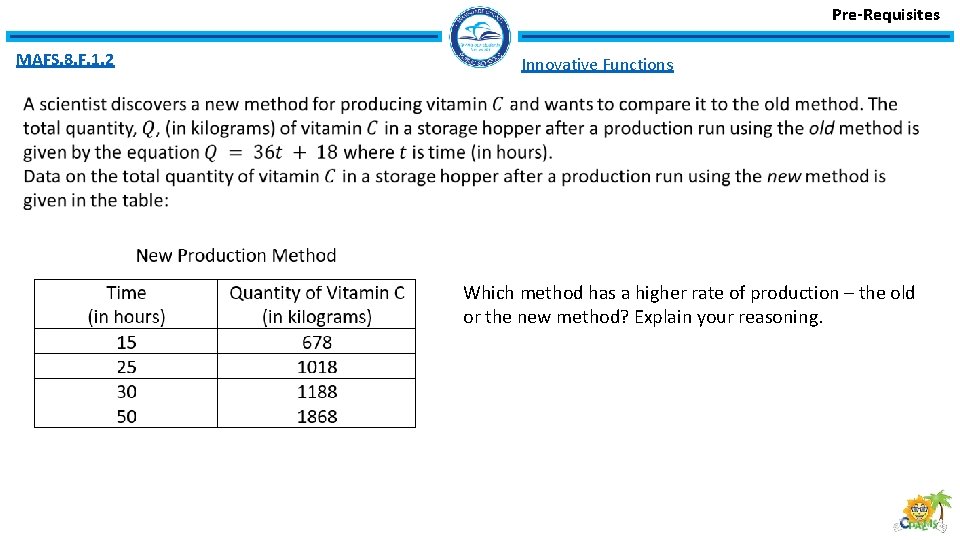
Pre-Requisites MAFS. 8. F. 1. 2 Innovative Functions Which method has a higher rate of production – the old or the new method? Explain your reasoning.

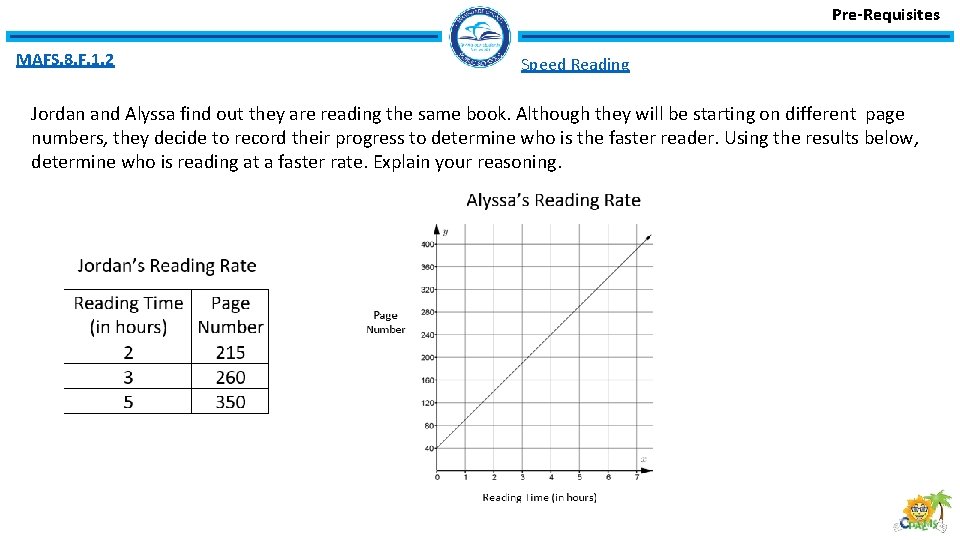
Pre-Requisites MAFS. 8. F. 1. 2 Speed Reading Jordan and Alyssa find out they are reading the same book. Although they will be starting on different page numbers, they decide to record their progress to determine who is the faster reader. Using the results below, determine who is reading at a faster rate. Explain your reasoning.

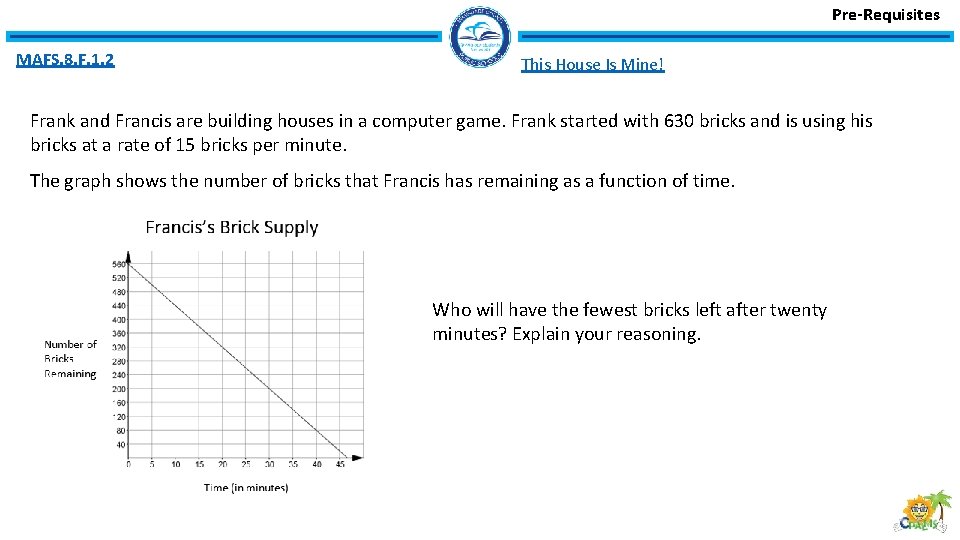
Pre-Requisites MAFS. 8. F. 1. 2 This House Is Mine! Frank and Francis are building houses in a computer game. Frank started with 630 bricks and is using his bricks at a rate of 15 bricks per minute. The graph shows the number of bricks that Francis has remaining as a function of time. Who will have the fewest bricks left after twenty minutes? Explain your reasoning.

Pre-Requisites MAFS. 8. F. 1. 2 Battery Charging Sam wants to take his MP 3 player and his video game player on a car trip. An hour before they plan to leave, he realized that he forgot to charge the batteries last night. At that point, he plugged in both devices so they can charge as long as possible before they leave. Sam knows that his MP 3 player has 40% of its battery life left and that the battery charges by an additional 12 percentage points every 15 minutes. His video game player is new, so Sam doesn’t know how fast it is charging but he recorded the battery charge for the first 30 minutes after he plugged it in. a. If Sam’s family leaves as planned, what percent of the battery will be charged for each of the two devices when they leave? b. How much time would Sam need to charge the battery 100% on both devices?

Pre-Requisites MAFS. 8. F. 2. 5 Bacterial Growth Graph Madison is studying the growth of bacteria in food and learned it has four phases. Label the axes and show a graph of the four stages, assuming an initial bacteria count of 50. • Lag Phase: Bacteria are introduced to the food, causing biochemical activity but no growth in the number of cells for the first hour. • Log Phase: Rapid exponential growth in the number of bacteria for the next two hours. • Stationary Phase: Growth stops for one hour as nutrients are used up and waste accumulates. • Death Phase: All bacteria gradually die off during the final four-hour phase.

Pre-Requisites MAFS. 8. F. 2. 5 Graph the Ride Sophia gets on her bike and accelerates until she reaches a constant speed, which she maintains for 10 minutes. She then reaches a large hill where her rate slows considerably. She maintains this slower rate for five minutes until she gets to the top of the hill where she stops. Sketch a graph that models the relationship between Sophia’s rate and the passage of time (from getting on her bike until stopping at the top of the hill). Be sure to label each axis with the appropriate variable.

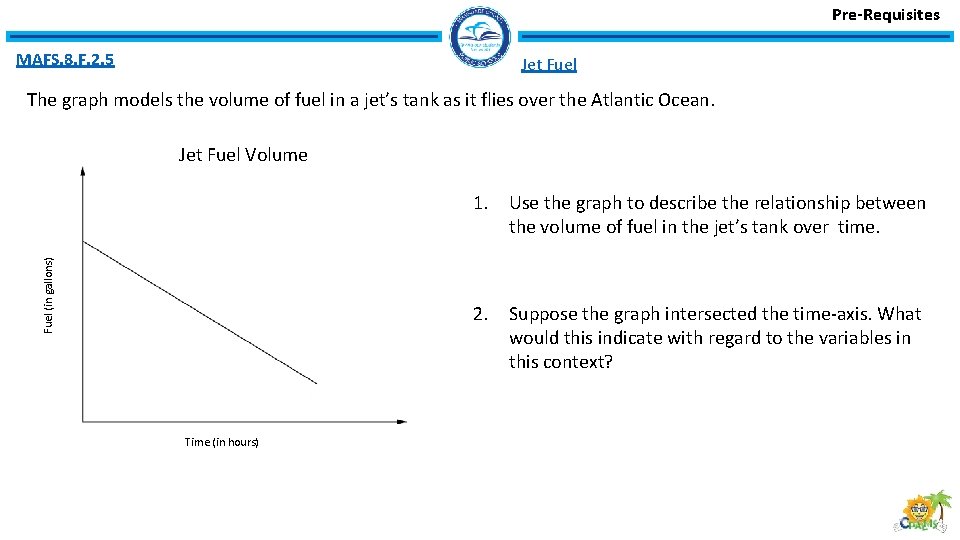
Pre-Requisites MAFS. 8. F. 2. 5 Jet Fuel The graph models the volume of fuel in a jet’s tank as it flies over the Atlantic Ocean. Jet Fuel Volume Fuel (in gallons) 1. Use the graph to describe the relationship between the volume of fuel in the jet’s tank over time. 2. Suppose the graph intersected the time-axis. What would this indicate with regard to the variables in this context? Time (in hours)

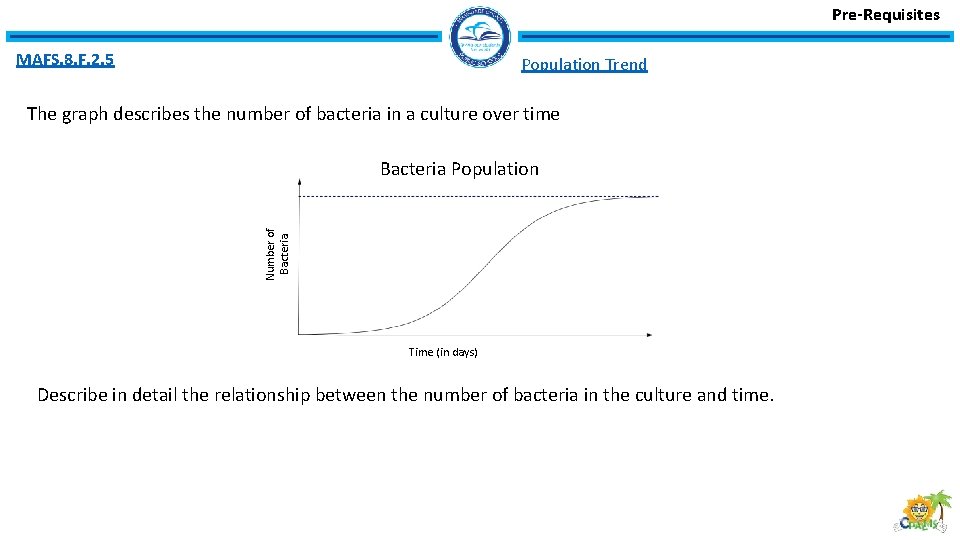
Pre-Requisites MAFS. 8. F. 2. 5 Population Trend The graph describes the number of bacteria in a culture over time Number of Bacteria Population Time (in days) Describe in detail the relationship between the number of bacteria in the culture and time.

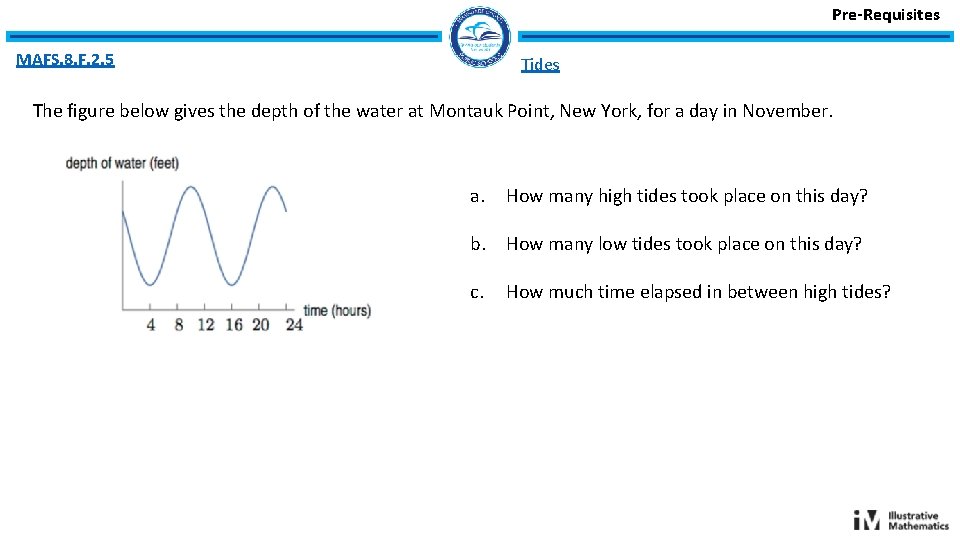
Pre-Requisites MAFS. 8. F. 2. 5 Tides The figure below gives the depth of the water at Montauk Point, New York, for a day in November. a. How many high tides took place on this day? b. How many low tides took place on this day? c. How much time elapsed in between high tides?

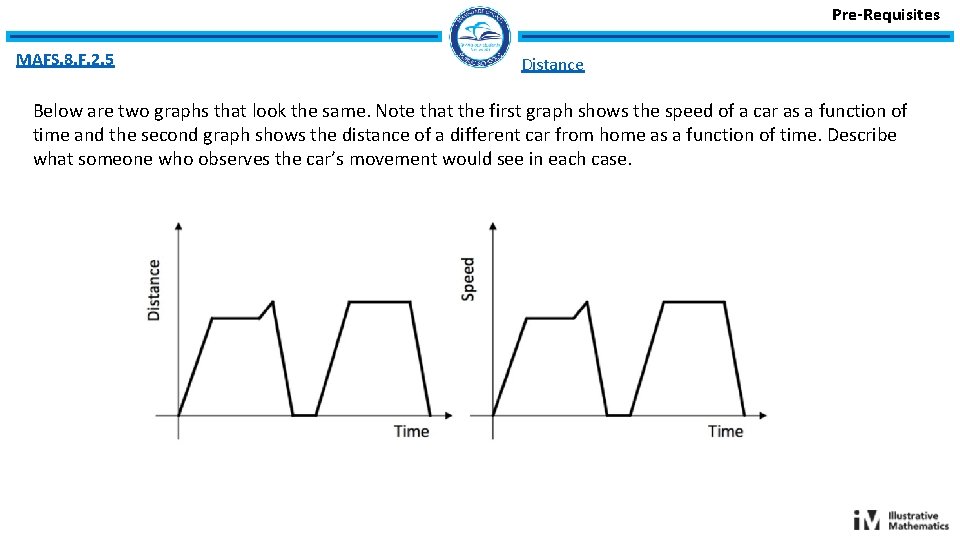
Pre-Requisites MAFS. 8. F. 2. 5 Distance Below are two graphs that look the same. Note that the first graph shows the speed of a car as a function of time and the second graph shows the distance of a different car from home as a function of time. Describe what someone who observes the car’s movement would see in each case.

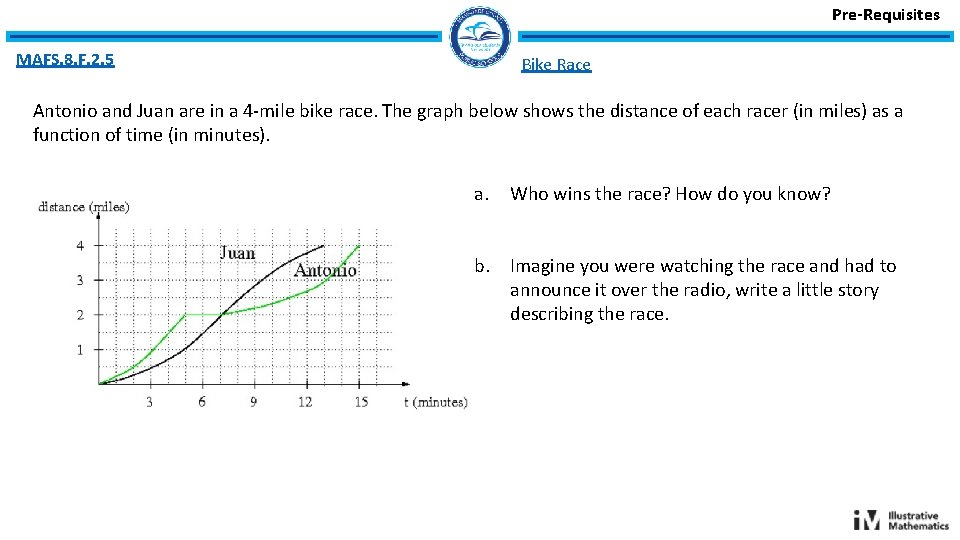
Pre-Requisites MAFS. 8. F. 2. 5 Bike Race Antonio and Juan are in a 4 -mile bike race. The graph below shows the distance of each racer (in miles) as a function of time (in minutes). a. Who wins the race? How do you know? b. Imagine you were watching the race and had to announce it over the radio, write a little story describing the race.

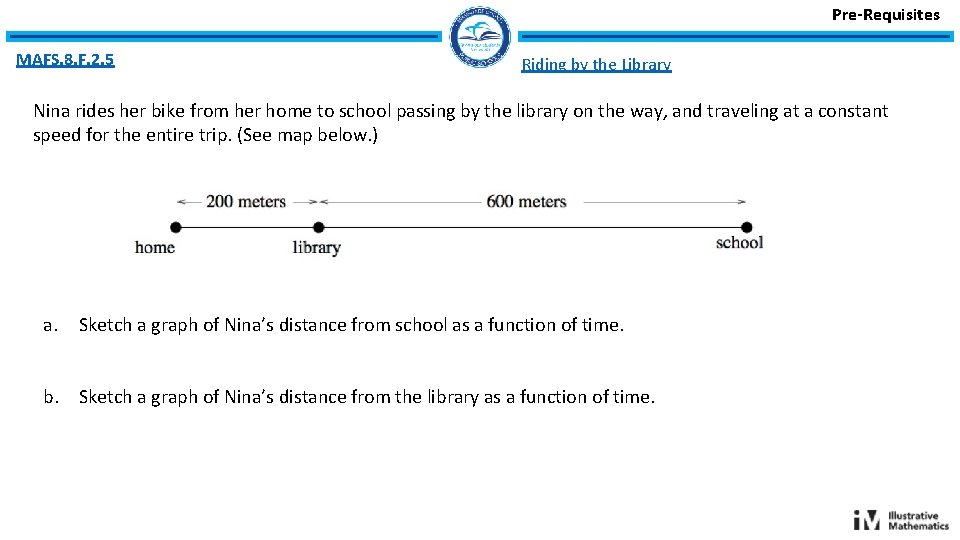
Pre-Requisites MAFS. 8. F. 2. 5 Riding by the Library Nina rides her bike from her home to school passing by the library on the way, and traveling at a constant speed for the entire trip. (See map below. ) a. Sketch a graph of Nina’s distance from school as a function of time. b. Sketch a graph of Nina’s distance from the library as a function of time.

Reporting Category Practice Items Topic 2

MAFS. 912. F-IF. 1. 2 & MAFS. 912. F-IF. 2. 4

MAFS. 912. F-BF. 1. 1 a She can afford to rent a movie using her rental card for 63 weeks.

MAFS. 912. F-BF. 1. 1 a Each day Shennie records the height of a plant for her science lab. Her data are shown in the table below. Day (n) Height (cm) 1 2 3 4 5 3. 0 4. 5 6. 0 7. 5 9. 0

MAFS. 912. F-BF. 1. 1 a & MAFS. 912. F-IF. 2. 5 A summer camp wants to take a field trip to the water park. They are taking a school bus that can hold 42 students. It will cost $25 to park the bus. Tickets to the water park are $18. 50 person. a) Write a function that models the total cost for the summer camp to go the water park. a) Identify and explain the domain for this scenario. The problem says that the bus can only hold 42 people, so I know that my domain has to be less than or equal to 42. However, since negative numbers are also less than 42 and I can’t have negative people. I have to have a lower limit on my domain of 0. Therefore, my domain is only integers {0 < n ≤ 42 } if only one bus is requested. Students might identify that if no one signs up there will be no trip. They may also recognize that if more than 42 students want to come, they could request another bus.

MAFS. 912. F-IF. 2. 5 D

MAFS. 912. F-IF. 1. 1 Which relation is not a function? A

MAFS. 912. F-IF. 1. 1 Does the table represent a function? If so, state the domain and range. If not, state why. -5 0 -4 2 0 10 3 16 Yes, it is a function. Domain {-5, -4, 0, 3} and Range {0, 2, 10, 16}

MAFS. 912. F-IF. 1. 1 Determine whether the following situations represent functions. Explain your reasoning. If the situation represents a function, give the domain and range. a) Each U. S. coin is mapped to its monetary value. Function; no coin has more than one monetary value. The domain is the set of all U. S. coins. The range is the set of monetary values assigned to each coin. b) A $1, $5, $10, $20, $50, or $100 bill is mapped to all the sets of coins that are the same total value as the bill. Not a function; each bill is equivalent to many different combinations of coins.

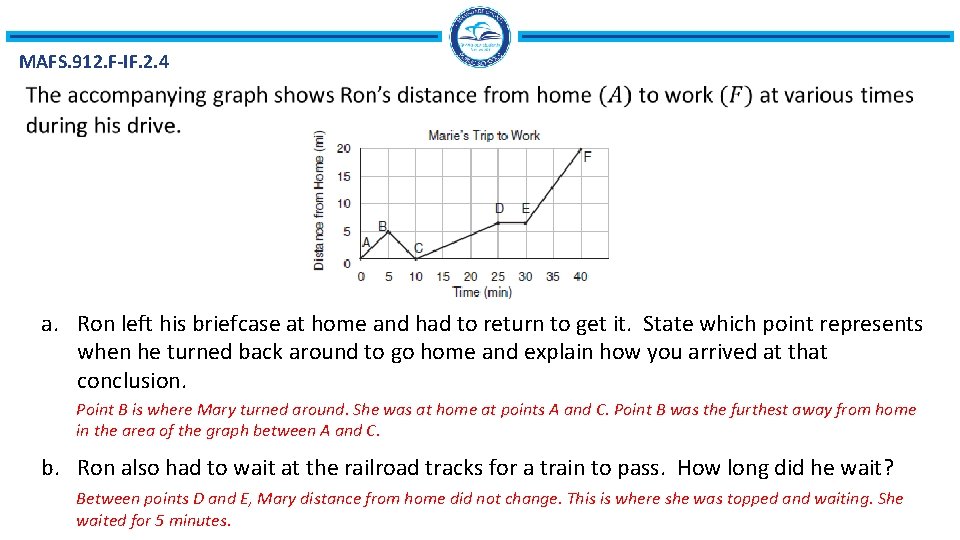
MAFS. 912. F-IF. 2. 4 a. Ron left his briefcase at home and had to return to get it. State which point represents when he turned back around to go home and explain how you arrived at that conclusion. Point B is where Mary turned around. She was at home at points A and C. Point B was the furthest away from home in the area of the graph between A and C. b. Ron also had to wait at the railroad tracks for a train to pass. How long did he wait? Between points D and E, Mary distance from home did not change. This is where she was topped and waiting. She waited for 5 minutes.

MAFS. 912. F-IF. 1. 2 At 1 hour the temperature of the ribs are 125 degrees Fahrenheit At 4 hours the temperature of the ribs is less than the temperature of the ribs at 7 hours. At 5 hours the temperature of the ribs is the same as the temperature of the ribs at 6 hours. During the smoking process the temperature will reach a maximum temperature.

MAFS. 912. F-IF. 1. 2

MAFS. 912. F-IF. 2. 5 & MAFS. 912. F-BF. 1. 1 a Lisa is planning to send out thank you cards from her birthday party. She needs to purchase one large box of 20 cards, and stamps for the cards that she sends. She created the table below to show much she will spend depending on the number of cards she sends out. # of Stamps Total Cost 5 $5. 75 10 $8. 00 15 $10. 25 20 $12. 50 a) What is an appropriate domain for this situation? Justify your answer. b) How much does one stamp cost? How much is the box of cards? One stamp costs $0. 45 and one pack of cards is $3. 50. c) Write the function that represent Lisa’s total cost depending on number of stamps needed. d) If Lisa planned to write 16 cards, how much will it cost her?

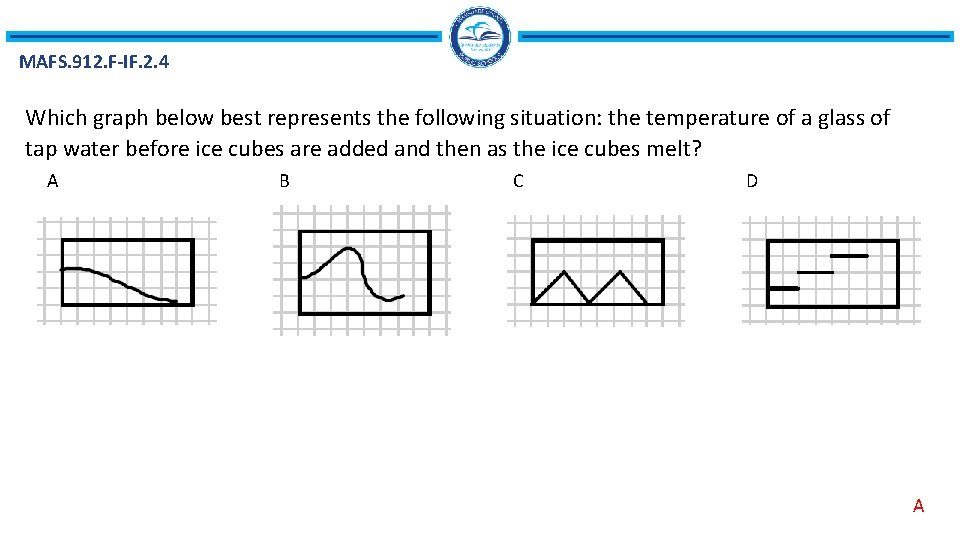
MAFS. 912. F-IF. 2. 4 Which graph below best represents the following situation: the temperature of a glass of tap water before ice cubes are added and then as the ice cubes melt? A B C D A

MAFS. 912. F-IF. 2. 5 Nonnegative integers.

MAFS. 912. F-IF. 2. 5 & MAFS. 912. F-BF. 1. 1 a A farmer market sells two brands of cheese by the pound. Brand A costs $4. 19 per pound, and brand B costs $4. 79 per pound. Brand A can be purchased in any amount, whereas brand B comes in prepackaged containers of either 0. 5 pound or 1 pound. Write a function rule that represents the revenue earned for each of the brands and determine a reasonable domain for each. Explain your answers.

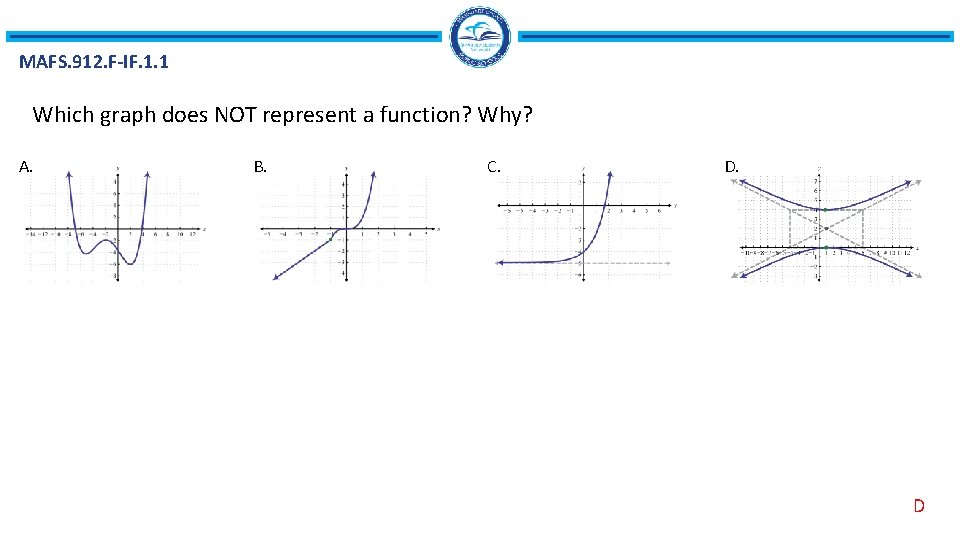
MAFS. 912. F-IF. 1. 1 Which graph does NOT represent a function? Why? A. B. C. D

MAFS. 912. F-BF. 1. 1 a Write a function to represent the table. -2 -4 -1 -1 0 2 1 5 2 8 A B C D D

MAFS. 912. F-IF. 2. 5

MAFS. 912. F-IF. 2. 6

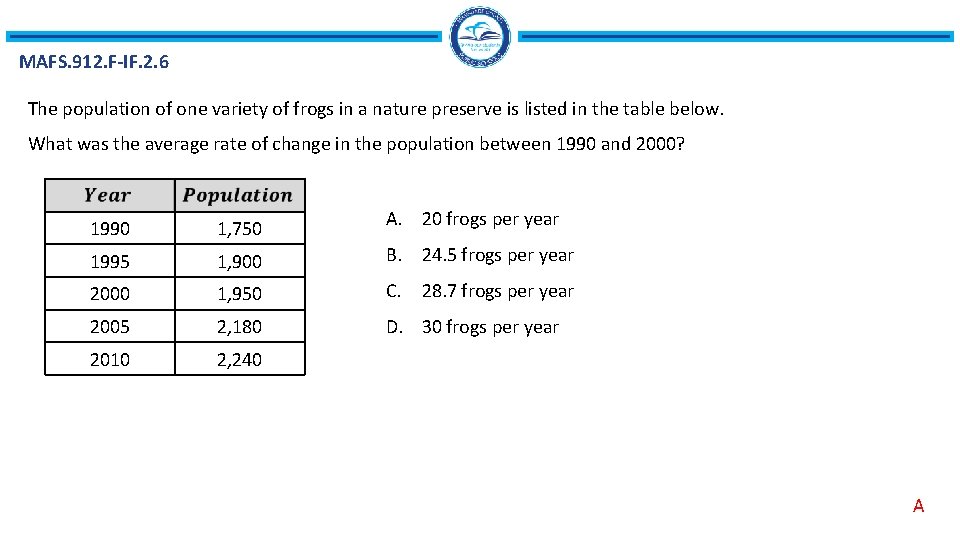
MAFS. 912. F-IF. 2. 6 The population of one variety of frogs in a nature preserve is listed in the table below. What was the average rate of change in the population between 1990 and 2000? 1990 1, 750 A. 20 frogs per year 1995 1, 900 B. 24. 5 frogs per year 2000 1, 950 C. 28. 7 frogs per year 2005 2, 180 D. 30 frogs per year 2010 2, 240 A

MAFS. 912. F-IF. 1. 3 Number of Seats Row Number Row 1 8 Row 2 11 Row 5 20 Row 10 35

MAFS. 912. F-BF. 1. 1 a The City of Altropolis is preparing for an upcoming marathon that will run throughout the city. The first four runs will be awarded cash prizes. First place will win the most and each place after will win $100 less than the previous place. Part A: Create a model that represents the total amount of cash needed to award the top four runners. Part B: The committee has raised enough money to award a total of $500 to only the first three winners. What amount will each of the three winners win? Justify your answer. $266. 66 for first place $166. 66 for second place $66. 66 for third place

MAFS. 912. F-IF. 1. 3 A theater has 60 seats in the first row, 68 seats in the second row, 76 seats in the third row, and so on in the same increasing pattern. If theater has 20 rows of seats, how many seats are in theater?

MAFS. 912. F-IF. 1. 3 A B C D D

MAFS. 912. F-IF. 1. 3 What is the first term in the arithmetic sequence _____, 9, _____, 33, 45? A. -3 B. -1 C. 3 D. 6 A

MAFS. 912. F-IF. 1. 2 It means that after 4 days 32 thousand people have Swine flu.

MAFS. 912. F-IF. 1. 3 During a free fall, a skydiver falls 16 feet in the first second, 48 feet in the 2 nd second, and 80 feet in the third second. If she continues to fall at this rate, how many feet will she fall during the 8 th second?

MAFS. 912. F-BF. 1. 1 b

MAFS. 912. F-BF. 1. 1 b The manufacturers are willing to produce 230, 000 smart watches.

MAFS. 912. F-BF. 1. 1 c Scenario 1 will save you $2. 50.

MAFS. 912. F-BF. 1. 1 c

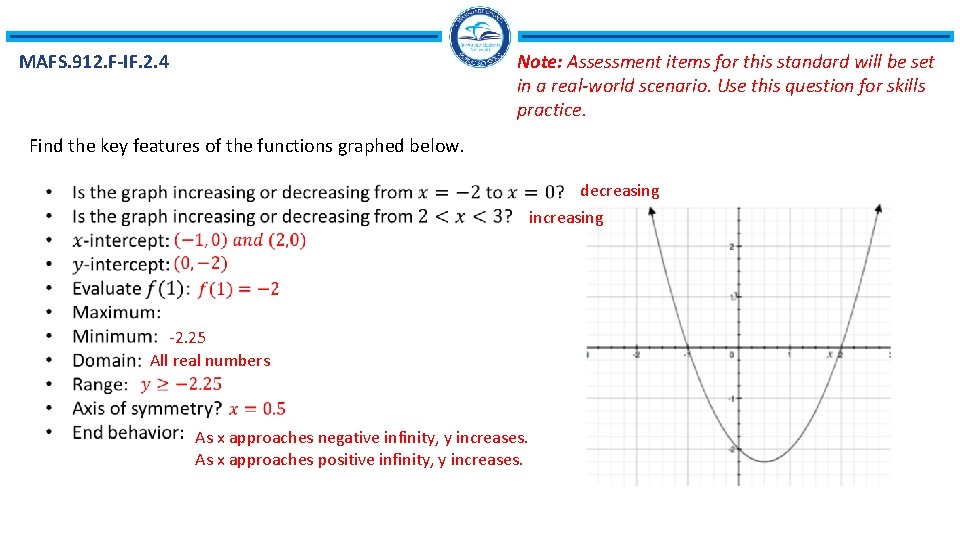
MAFS. 912. F-IF. 2. 4 Note: Assessment items for this standard will be set in a real-world scenario. Use this question for skills practice. Find the key features of the functions graphed below. decreasing increasing -2. 25 All real numbers As x approaches negative infinity, y increases. As x approaches positive infinity, y increases.

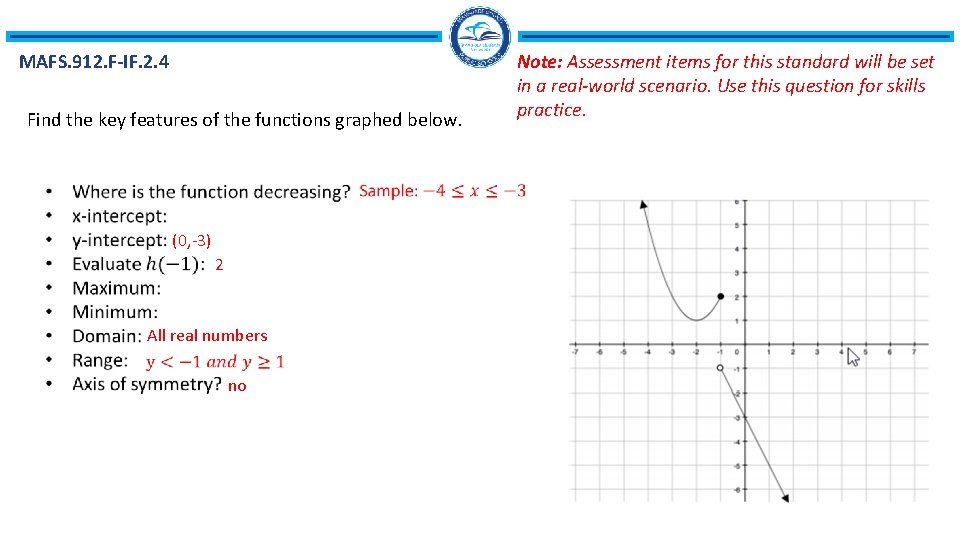
MAFS. 912. F-IF. 2. 4 Find the key features of the functions graphed below. (0, -3) 2 All real numbers no Note: Assessment items for this standard will be set in a real-world scenario. Use this question for skills practice.

MAFS. 912. F-IF. 2. 4 Find the key features of the functions graphed below. Note: Assessment items for this standard will be set in a real-world scenario. Use this question for skills practice. increasing All real numbers As x approaches negative infinity, y decreases. As x approaches positive infinity, y decreases.

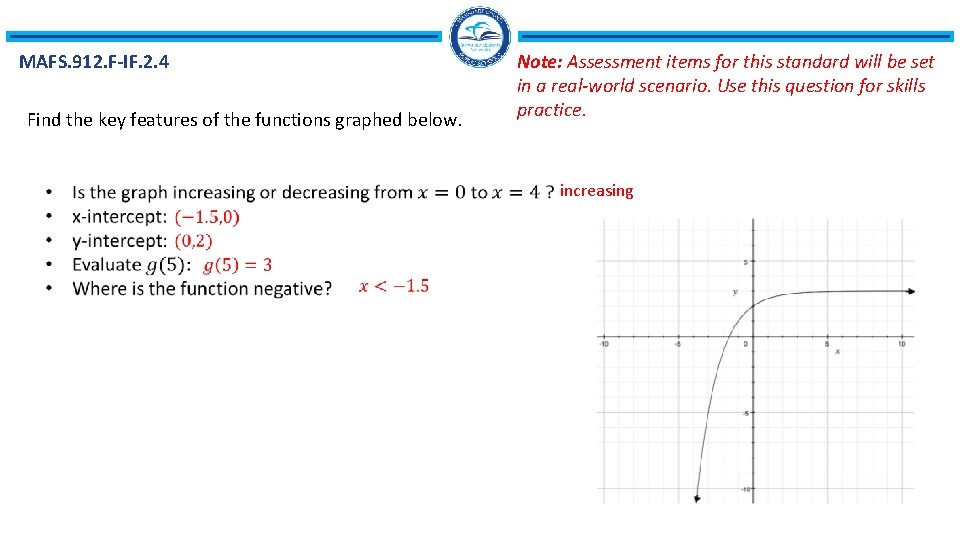
MAFS. 912. F-IF. 2. 4 Find the key features of the functions graphed below. Note: Assessment items for this standard will be set in a real-world scenario. Use this question for skills practice. increasing