EET 103 Chapter 3 Lecture 1 Three Phase






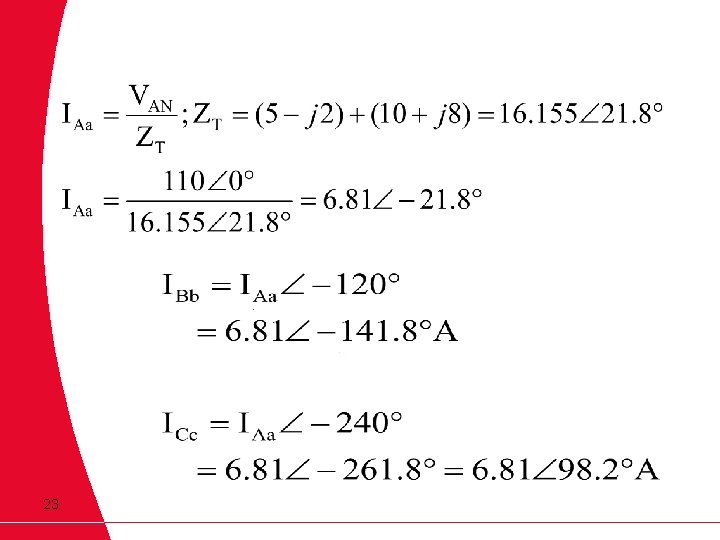

































- Slides: 76

EET 103 Chapter 3 (Lecture 1) Three Phase System

INTRODUCTION TO THREE PHASE SYSTEM In general, three phase systems are preferred over single phase systems for the transmission of the power system for many reasons, including the following • Thinner conductors can be used to transmit the same k. VA at the same voltage, which reduces the amount of copper required (typically about 25% less) and turn reduces construction and maintenance costs.

• The lighter lines are easier to install and the supporting structures can be less massive and farther apart. • In general, most larger motors are three phase because they are essentially self starting and do not require a special design or additional starting circuitry.

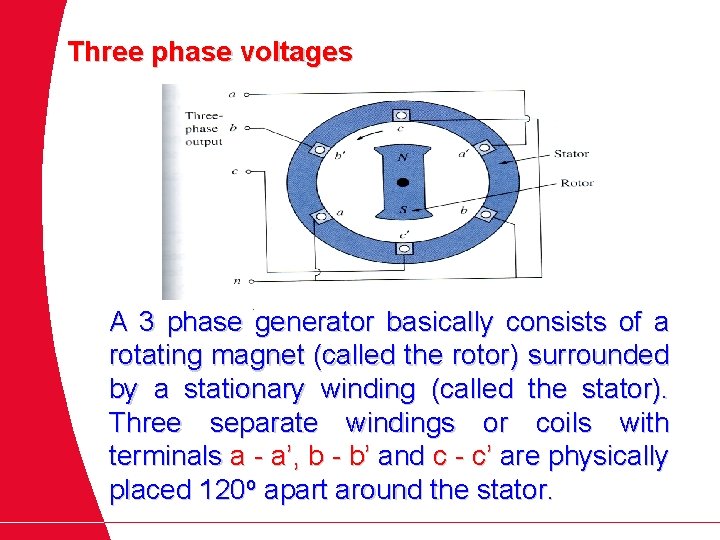
Three phase voltages A 3 phase generator basically consists of a rotating magnet (called the rotor) surrounded by a stationary winding (called the stator). Three separate windings or coils with terminals a - a’, b - b’ and c - c’ are physically placed 120 o apart around the stator.

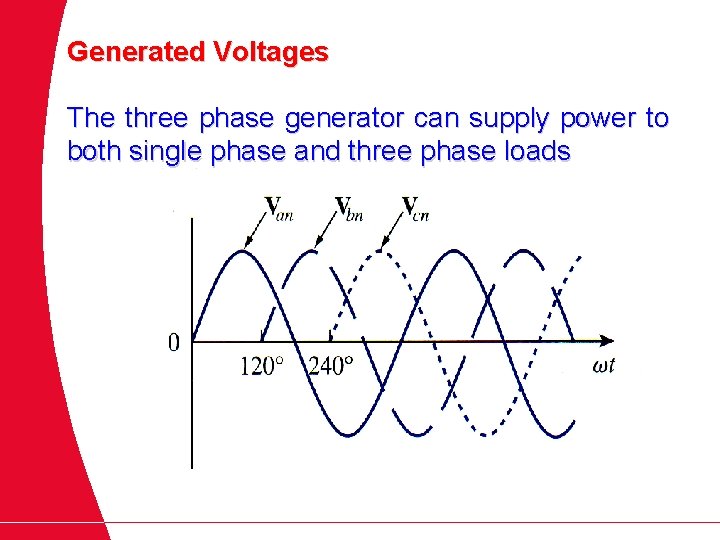
Generated Voltages The three phase generator can supply power to both single phase and three phase loads

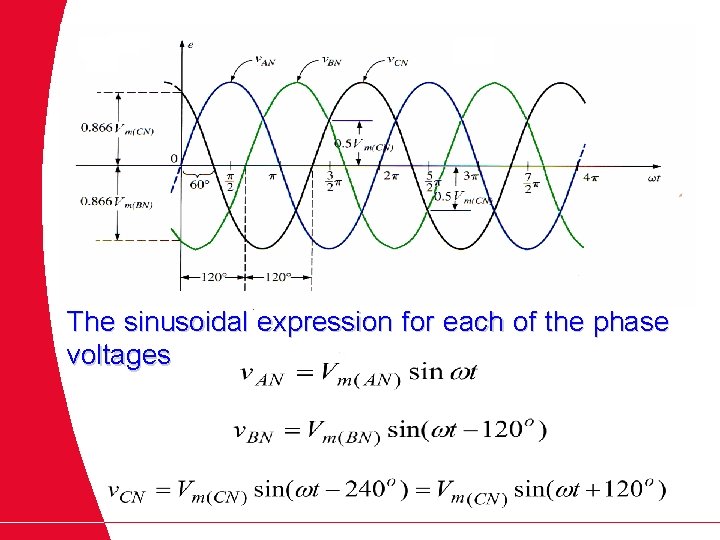
The sinusoidal expression for each of the phase voltages

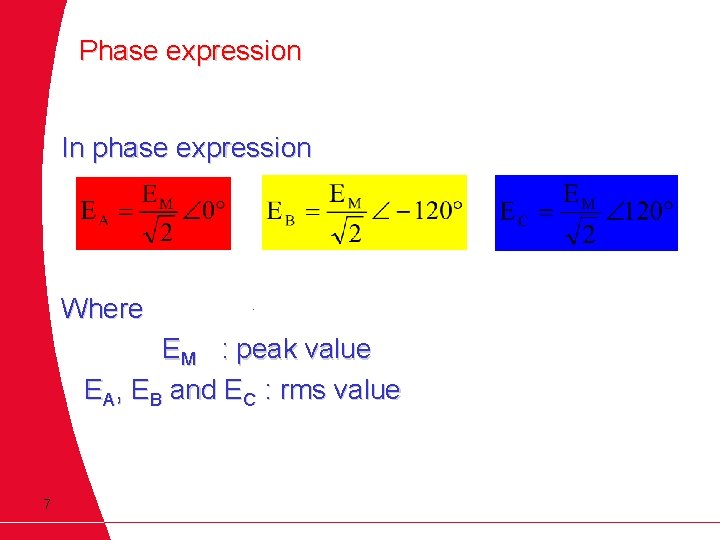
Phase expression In phase expression Where EM : peak value EA, EB and EC : rms value 7

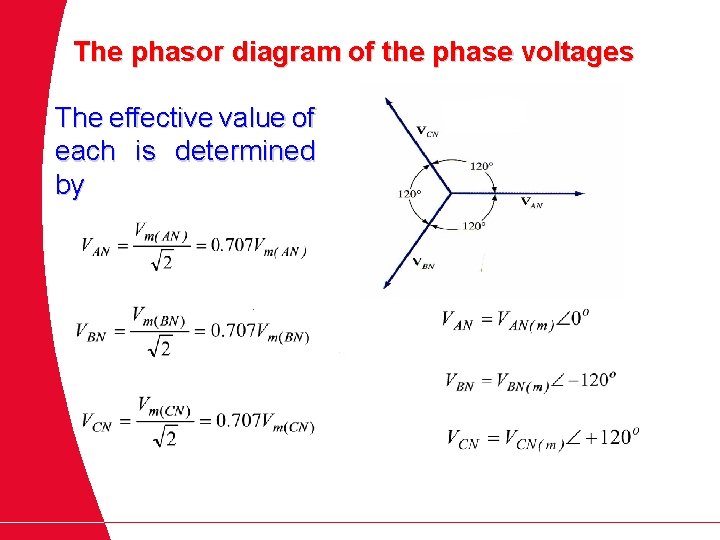
The phasor diagram of the phase voltages The effective value of each is determined by

If the voltage sources have the same amplitude and frequency ω and are out of the phase with each other by 120 o, the voltages are said to be balanced. By rearranging the phasors as shown in figure below, so Where

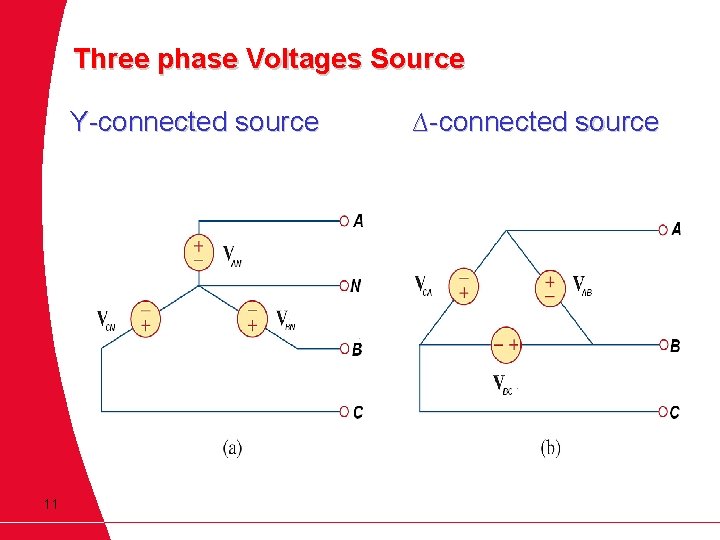
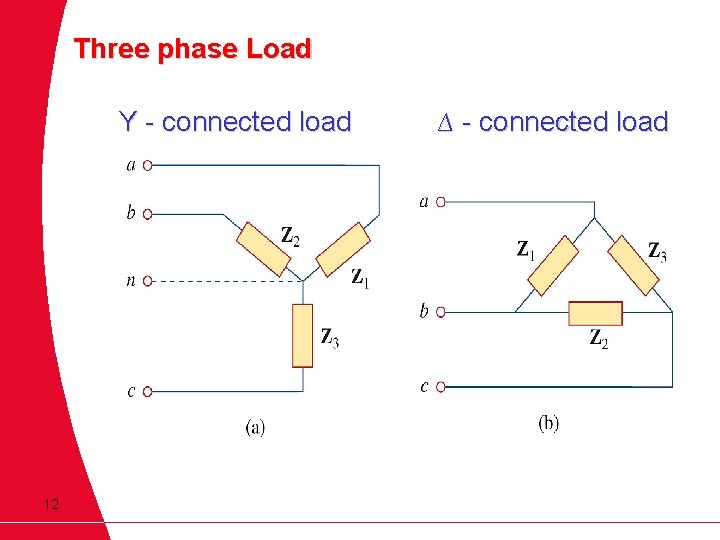
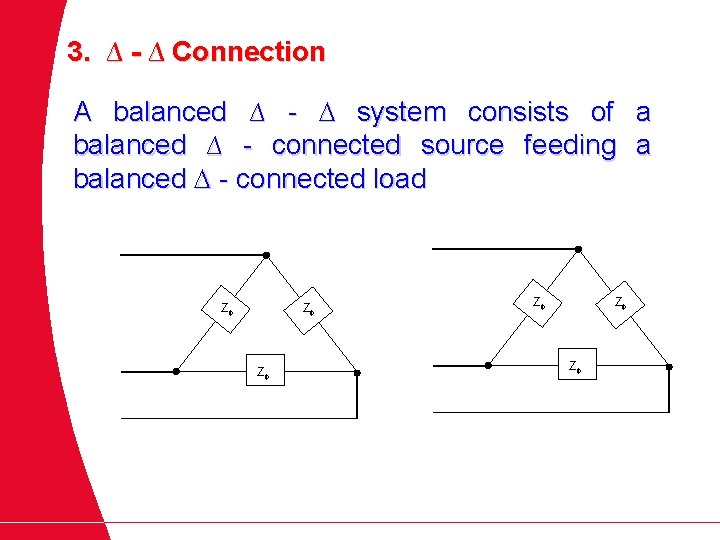
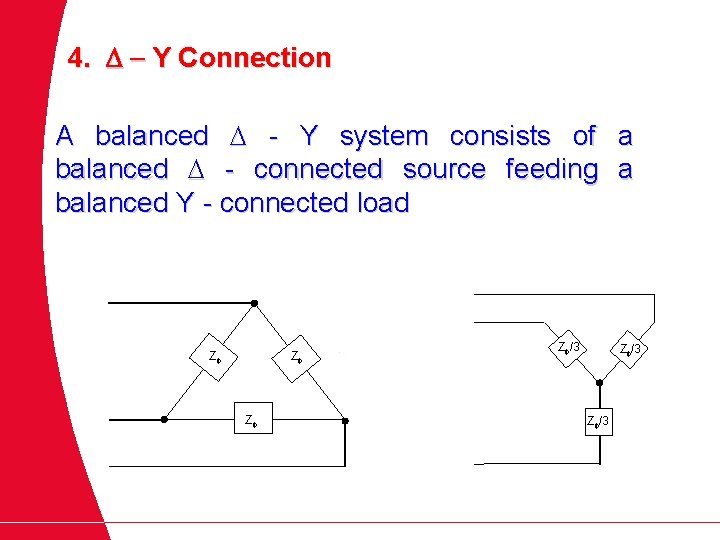
Connection in Three Phase System A 3 phase system is equivalent to three single phase circuit Two possible configurations in three phase system 1. Y - connection (star connection) 2. ∆ - connection (delta connection) 10

Three phase Voltages Source Y-connected source 11 ∆-connected source

Three phase Load Y - connected load 12 ∆ - connected load

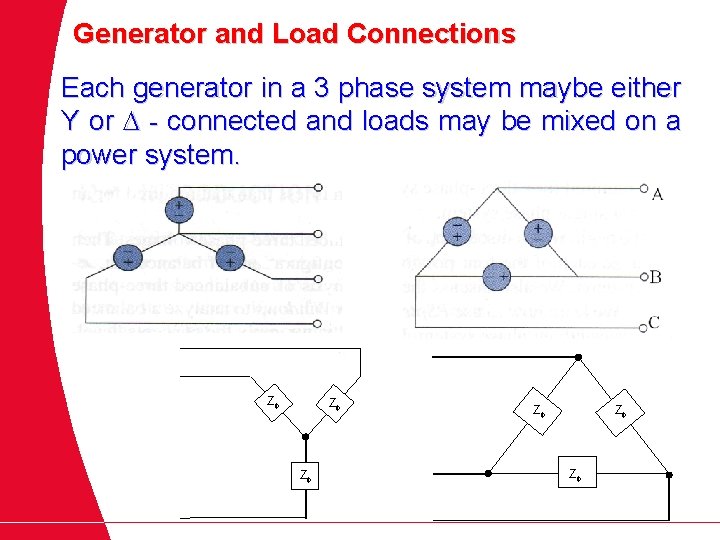
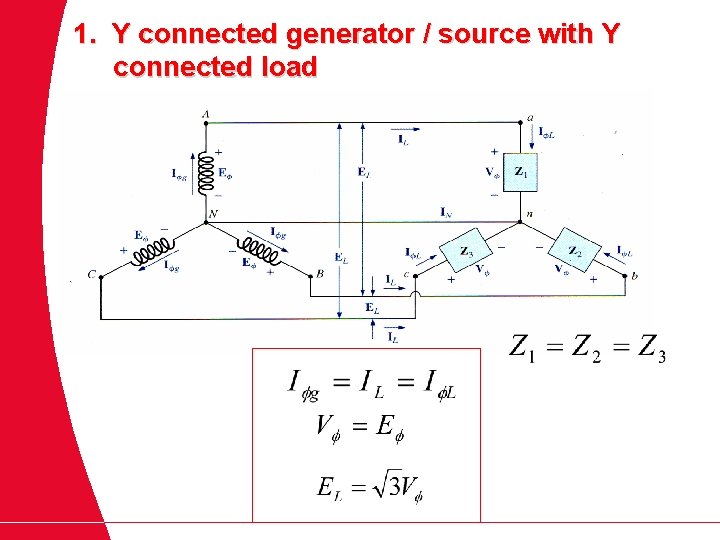
Generator and Load Connections Each generator in a 3 phase system maybe either Y or - connected and loads may be mixed on a power system. Z Z Z

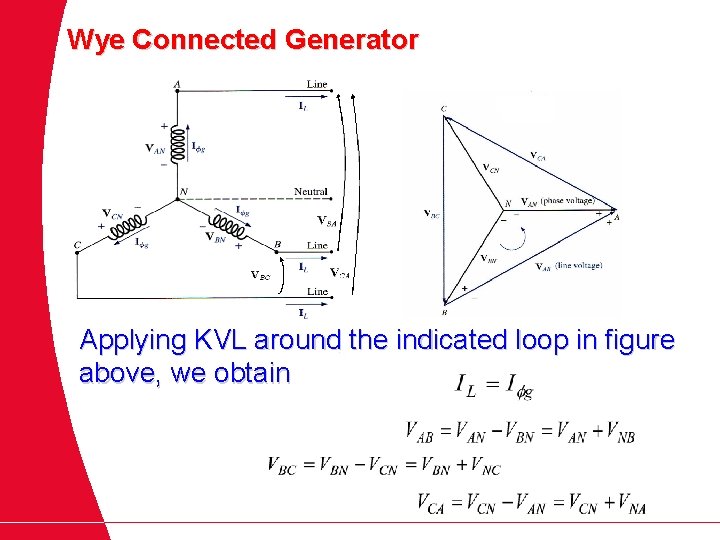
Wye Connected Generator Applying KVL around the indicated loop in figure above, we obtain

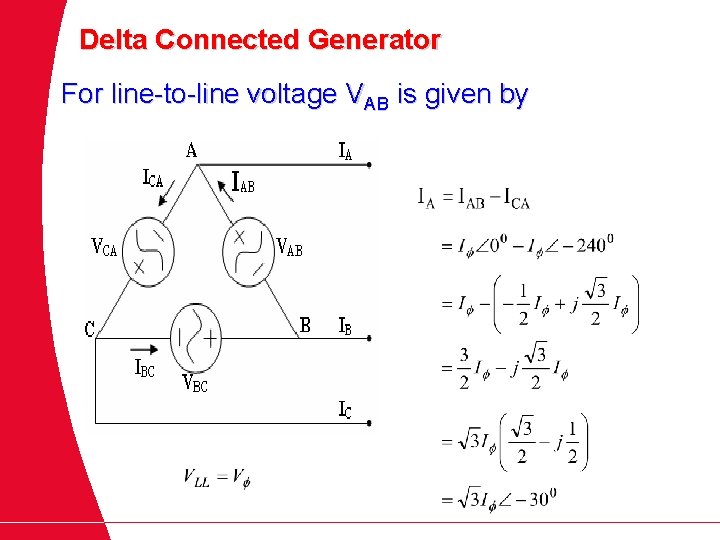
For line-to-line voltage VAB is given by

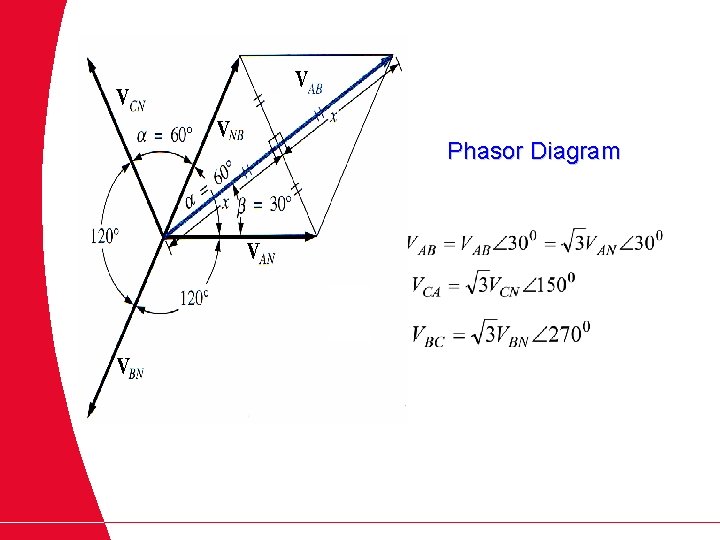
Phasor Diagram

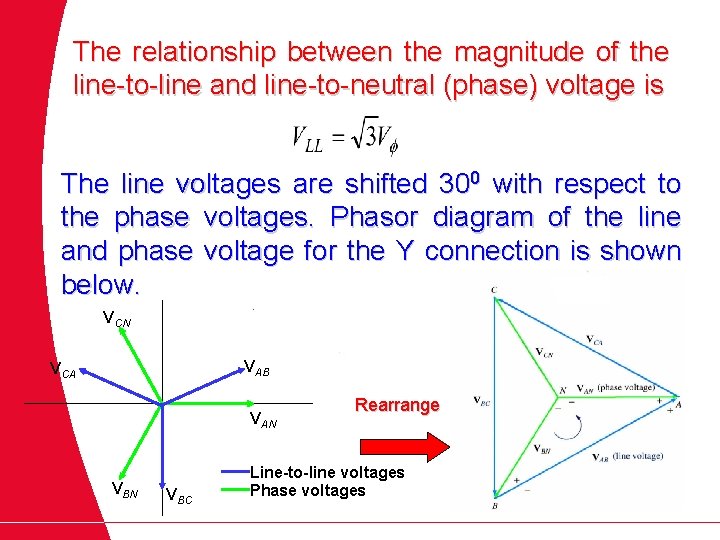
The relationship between the magnitude of the line-to-line and line-to-neutral (phase) voltage is The line voltages are shifted 300 with respect to the phase voltages. Phasor diagram of the line and phase voltage for the Y connection is shown below. VCN VAB VCA VAN VBC Rearrange Line-to-line voltages Phase voltages

Delta Connected Generator For line-to-line voltage VAB is given by

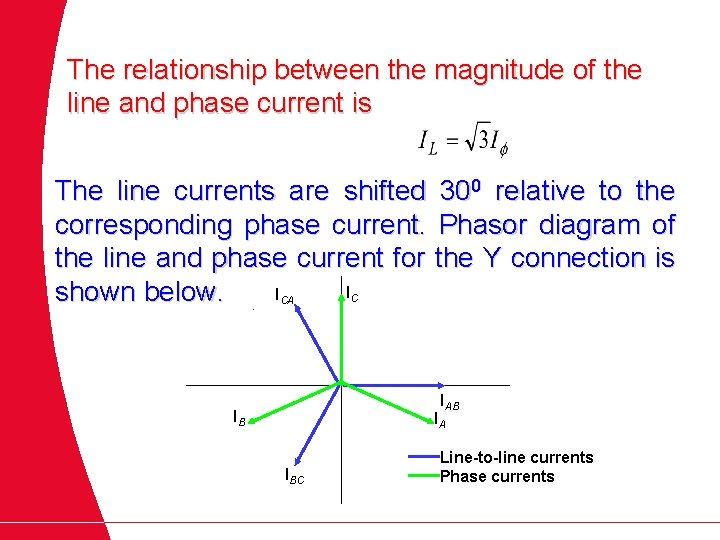
The relationship between the magnitude of the line and phase current is The line currents are shifted 300 relative to the corresponding phase current. Phasor diagram of the line and phase current for the Y connection is I I shown below. CA C IAB IB IA IBC Line-to-line currents Phase currents

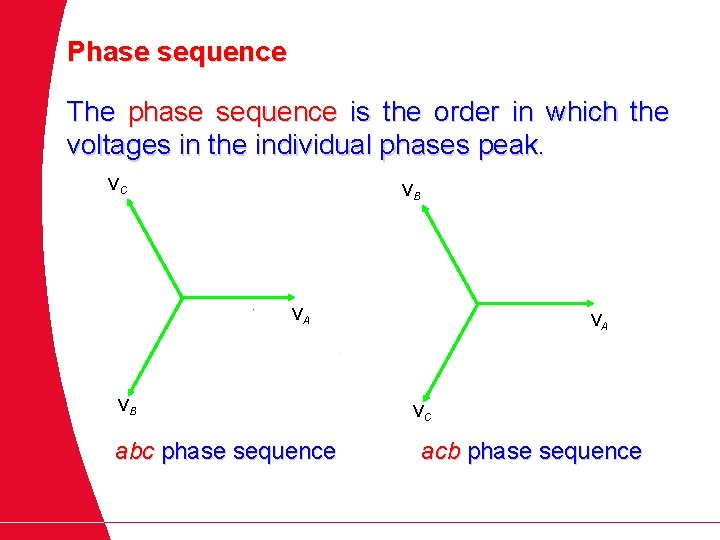
Phase sequence The phase sequence is the order in which the voltages in the individual phases peak. VC VB VA VB abc phase sequence VA VC acb phase sequence

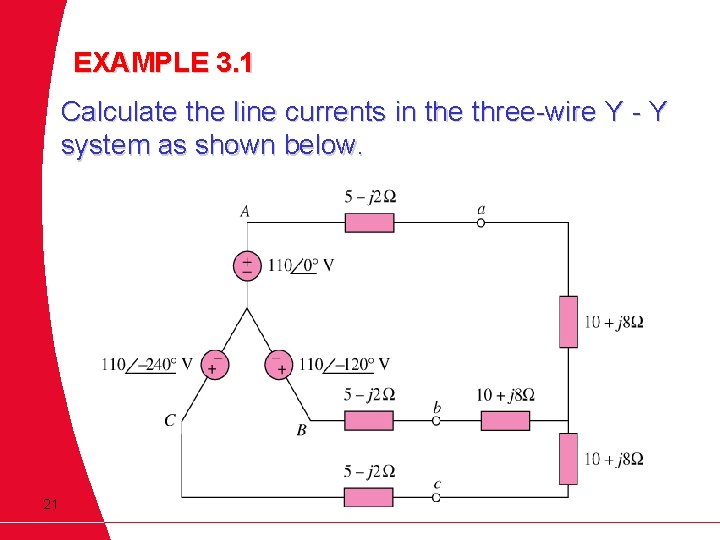
EXAMPLE 3. 1 Calculate the line currents in the three-wire Y - Y system as shown below. 21

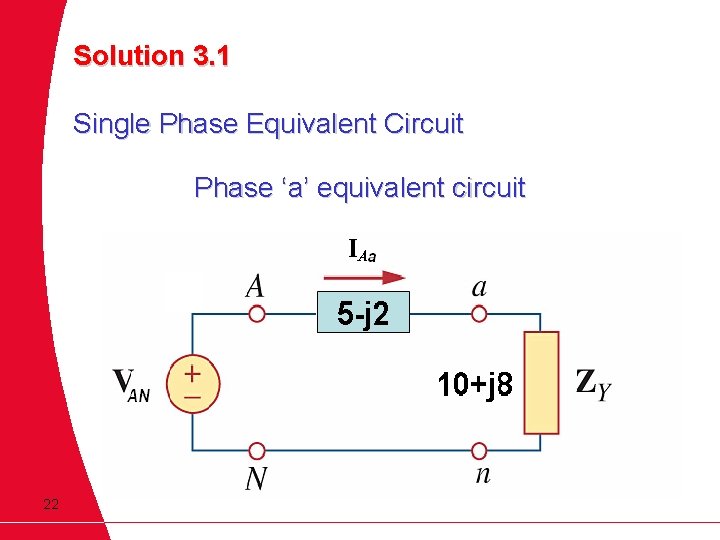
Solution 3. 1 Single Phase Equivalent Circuit Phase ‘a’ equivalent circuit 22
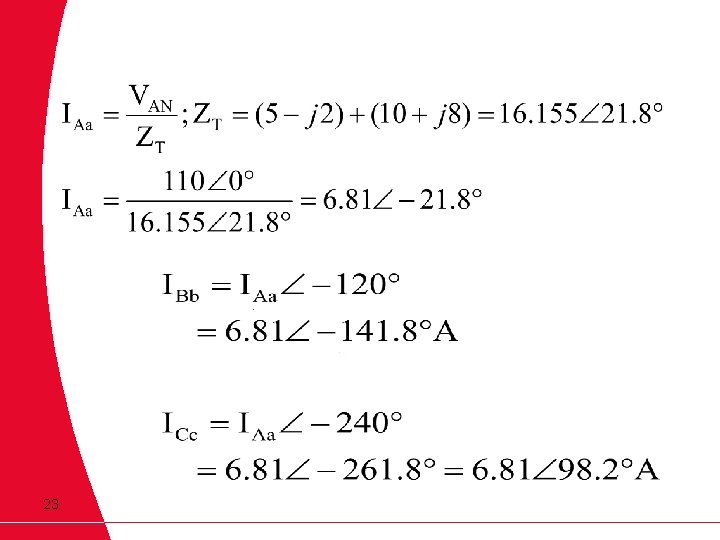
23

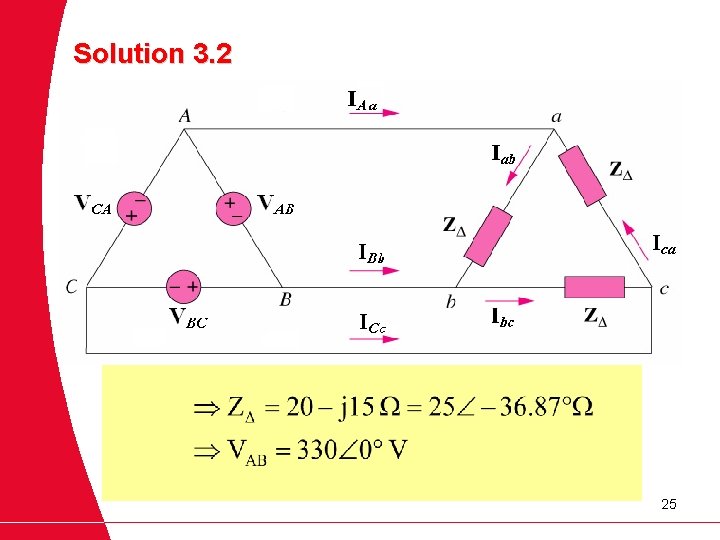
EXAMPLE 3. 2 A balanced delta connected load having an impedance 20 - j 15 is connected to a delta connected, positive sequence generator having VAB = 330 0 V. Calculate the phase currents of the load and the line currents. 24

Solution 3. 2 25

Phase Currents 26

Line Currents 27

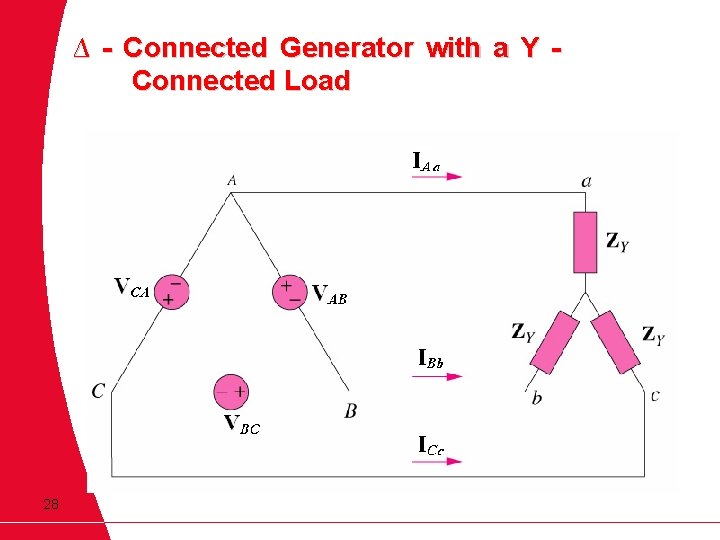
∆ - Connected Generator with a Y Connected Load 28

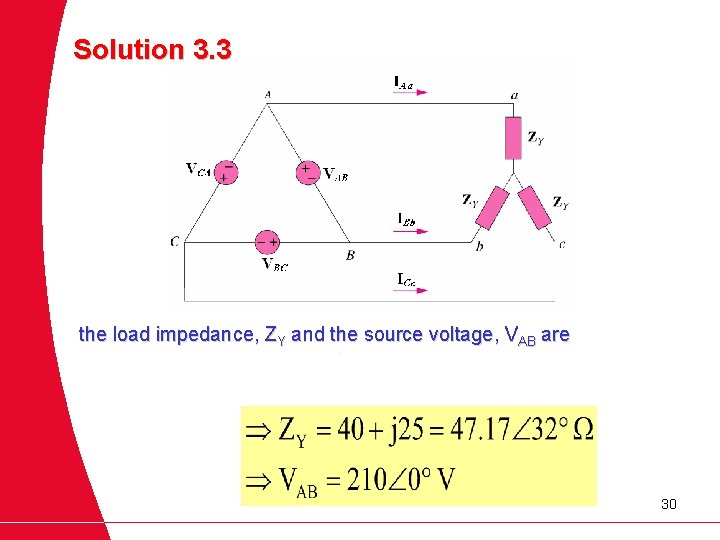
EXAMPLE 3. 3 A balanced Y - connected load with a phase impedance 40 + j 25 is supplied by a balanced, positive-sequence Δ-connected source with a line voltage of 210 V. Calculate the phase currents. Use VAB as reference. 29

Solution 3. 3 the load impedance, ZY and the source voltage, VAB are 30

When the ∆ - connected source is transformed to a Y - connected source, 31

The line currents are 32

Summary of Relationships in Y and ∆ - connections Y-connection Voltage magnitudes Current magnitudes Phase sequence ∆-connection VL leads Vφ by IL lags Iφ by 30° 33

EET 103 Chapter 3 (Lecture 2) Three Phase System

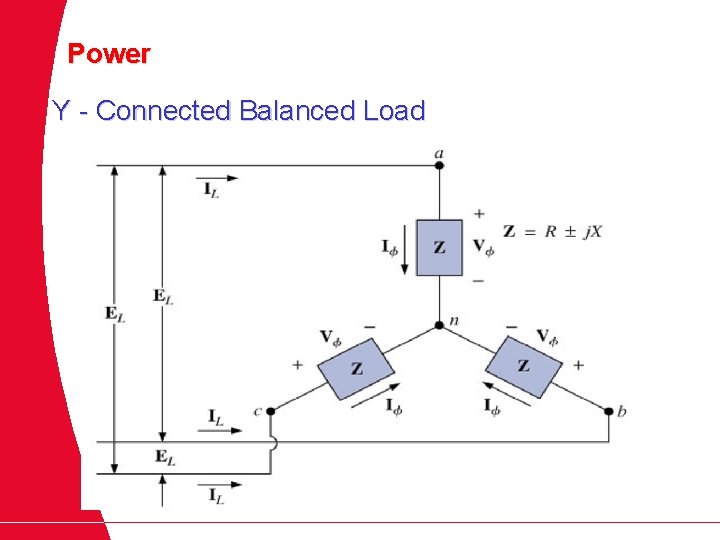
Power Y - Connected Balanced Load

Average Power The average power delivered to each phase The total power to the balanced load is

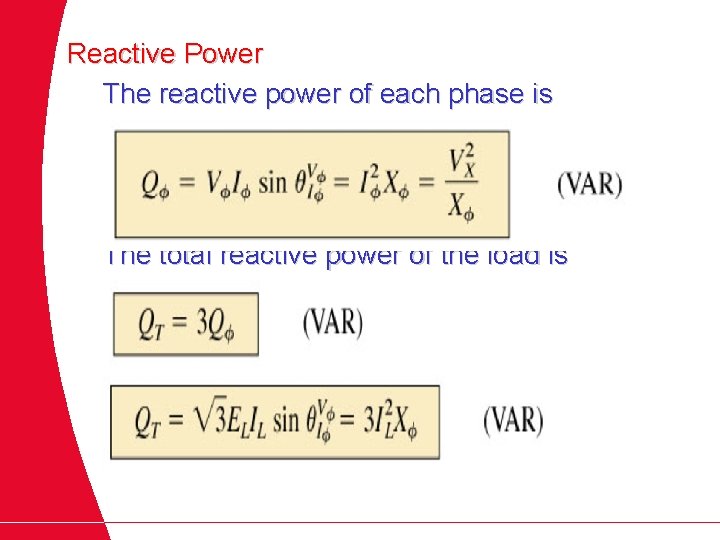
Reactive Power The reactive power of each phase is The total reactive power of the load is

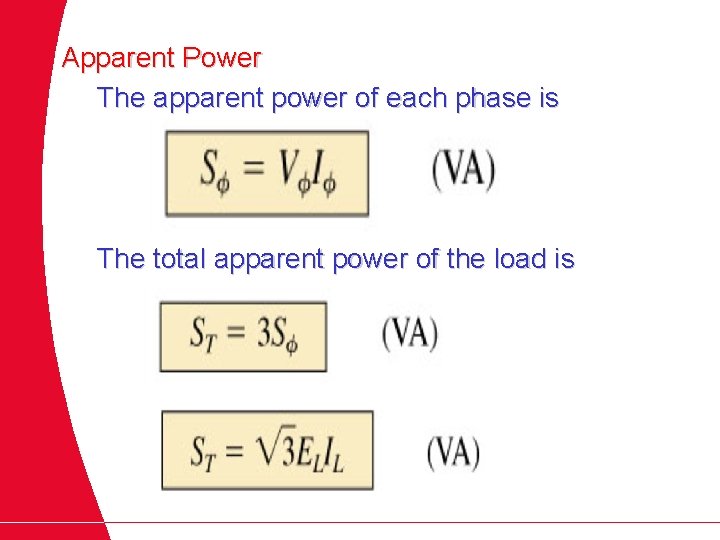
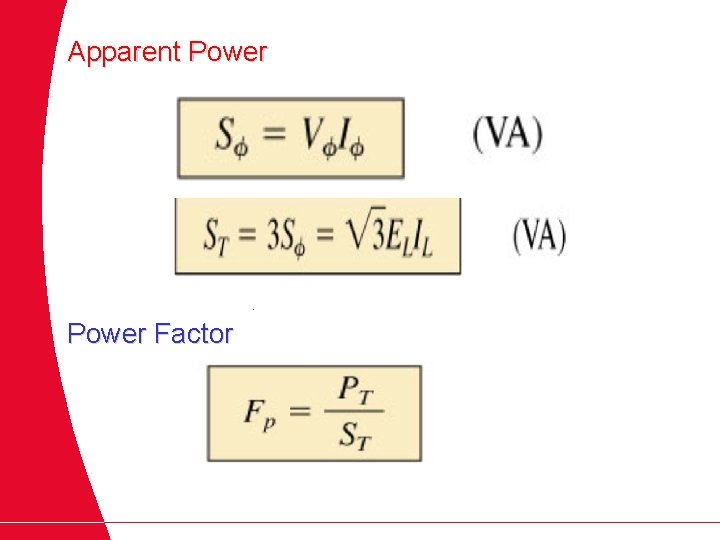
Apparent Power The apparent power of each phase is The total apparent power of the load is

Power Factor The power factor of the system is

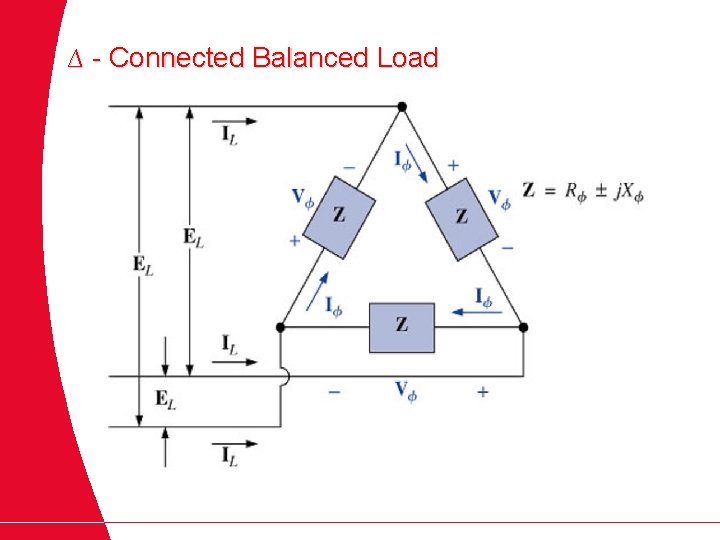
∆ - Connected Balanced Load

Average Power Reactive Power

Apparent Power Factor

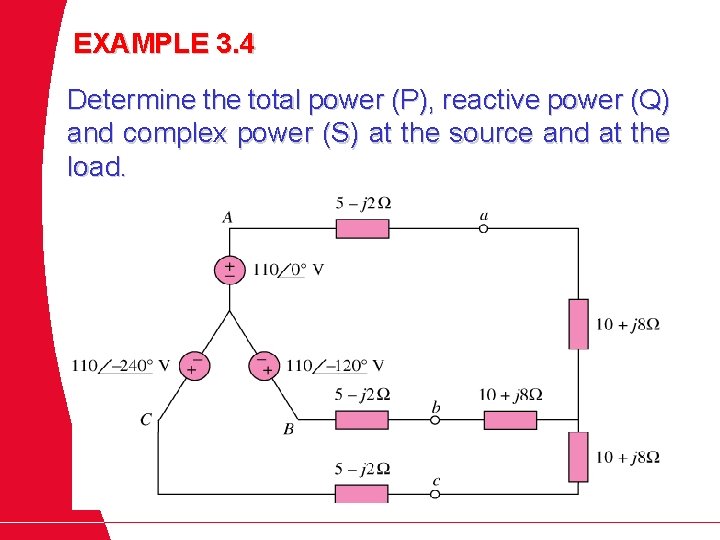
EXAMPLE 3. 4 Determine the total power (P), reactive power (Q) and complex power (S) at the source and at the load.

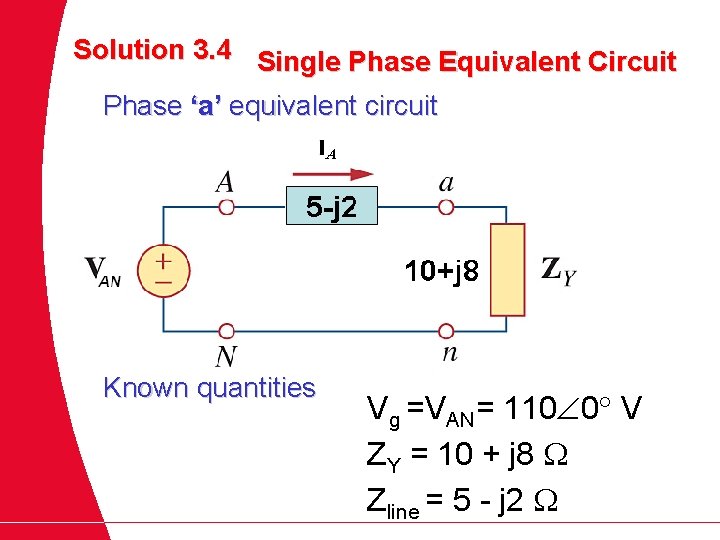
Solution 3. 4 Single Phase Equivalent Circuit Phase ‘a’ equivalent circuit Known quantities Vg =VAN= 110 0 V ZY = 10 + j 8 Zline = 5 - j 2

Line / Phase Currents

Source & Load Power

EXAMPLE 3. 5 A three phase motor can be regarded as a balanced Y - load. A three phase motor draws 5. 6 k. W when the line voltage is 220 V and the line current is 18. 2 A. Determine the power factor of the motor Known Quantities • PLoad = 5600 W • VL = 220 V • IL = 18. 2 A

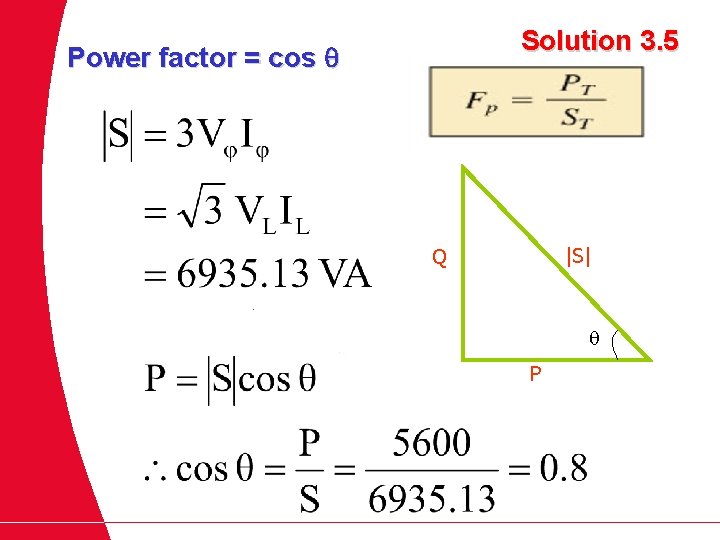
Solution 3. 5 Power factor = cos |S| Q P

Example 3. 6 For the Y - connected load in Figure a) find the average power to each phase and the total load b) determine the reactive power to each phase and the total reactive power c) find the apparent power to each phase and the total apparent power d) find the power factor of the load

Figure

Solution 3. 6 a) The average power to each phase is Total load

b) The reactive power to each phase is Total reactive power

c) The apparent power to each phase is Total apparent power

d) The power factor

Power relationship - Phase quantities The power equations applied to Y-or - load in a balanced 3 -phase system are Real power Watts (W) Reactive power Volt-Amps-Reactive (VAR) Apparent power Volt-Amps (VA) - angle between voltage and current in any phase of the load

Power relationship - Line quantities The power equations applied to Y-or - load in a balanced 3 -phase system are Real power Reactive power Apparent power - angle between phase voltage and phase current in any phase of the load

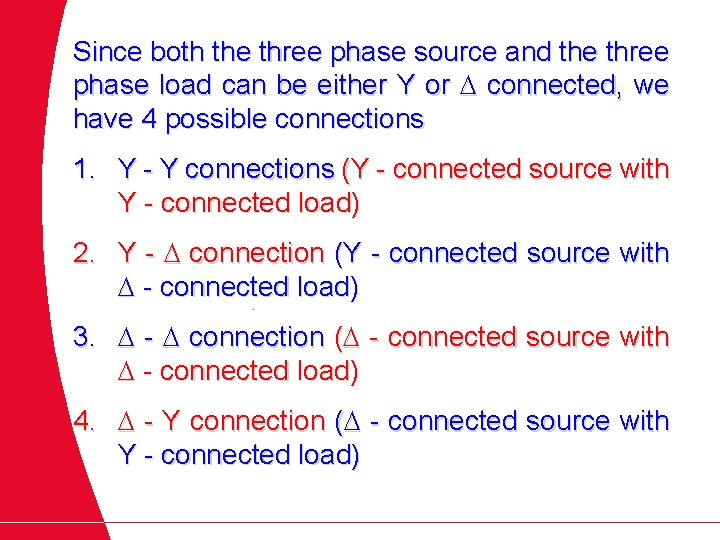
Since both the three phase source and the three phase load can be either Y or connected, we have 4 possible connections 1. Y - Y connections (Y - connected source with Y - connected load) 2. Y - connection (Y - connected source with - connected load) 3. - connection ( - connected source with - connected load) 4. - Y connection ( - connected source with Y - connected load)

1. Y connected generator / source with Y connected load

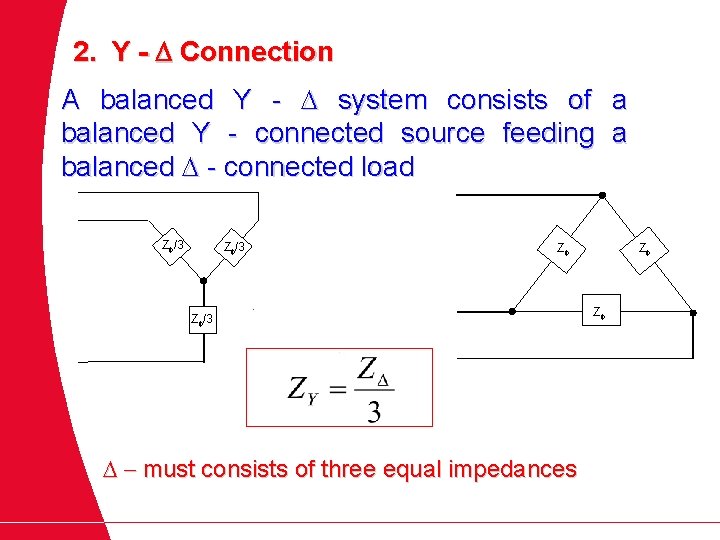
2. Y - D Connection A balanced Y - system consists of a balanced Y - connected source feeding a balanced - connected load Z /3 Z Z /3 - must consists of three equal impedances Z Z

3. ∆ - ∆ Connection A balanced ∆ - system consists of a balanced ∆ - connected source feeding a balanced - connected load Z Z Z

4. D - Y Connection A balanced - Y system consists of a balanced - connected source feeding a balanced Y - connected load Z Z /3

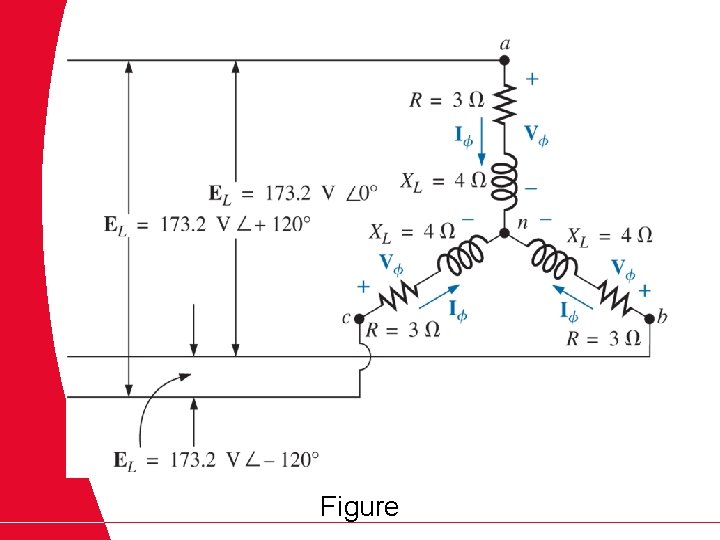
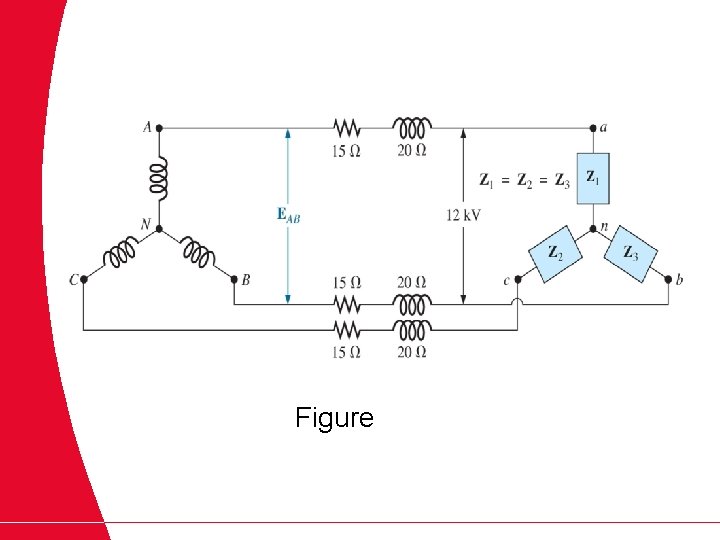
Example 3. 7 Each transmission line of the 3 wire, three phase system in Figure has an impedance of 15 Ω + j 20 Ω. The system delivers a total power of 160 k. W at 12, 000 V to a balanced three-phase load with a lagging power factor of 0. 86. a. Determine the magnitude of the line voltage EAB of the generator. b. Find the power factor of the total load applied to the generator. c. What is the efficiency of the system?

Figure

Solution 3. 7 a. Vø (load) = PT (load) = 3 Vø Iø cos θ and Since θ = cos-1 0. 86 = 30. 68 o (lagging) And assigning factor results in , a lagging power

For each phase, the system will appear as shown in figure below. Or Then

b. And c. < 0. 86 of load

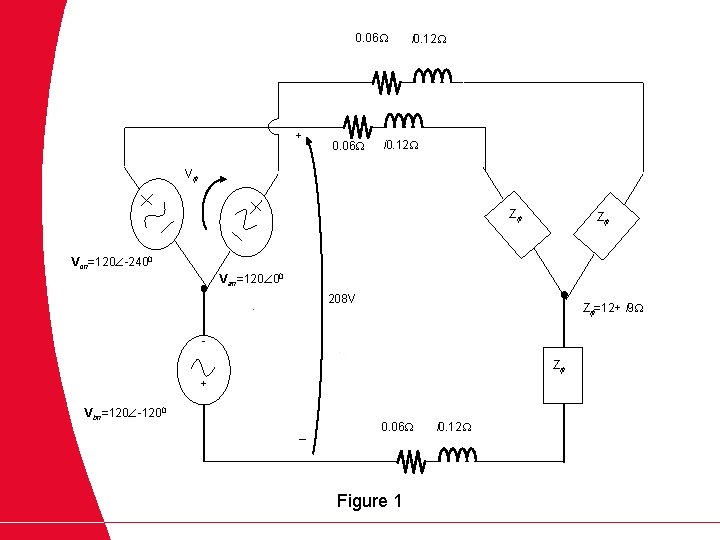
Example 3. 8 A 208 V three phase power system is shown in Figure 1. It consists of an ideal 208 V Y - connected three phase generator connected to a three phase transmission line to a Y - connected load. The transmission line has an impedance of 0. 06 + j 0. 12 W per phase and the load has an impedance of 12 + j 9 W per phase. For this simple system, find (a) The magnitude of the line current IL (b) The magnitude of the load’s line and phase voltages VLL and V L (c) The real, reactive and apparent powers consumed by the load (d) The power factor of the load (e) The real, reactive and apparent powers consumed by the transmission line (f) The real, reactive and apparent powers supplied by the generator (g) The generator’s power factor

0. 06 + 0. 06 i 0. 12 V Z Z Vcn=120 -2400 Van=120 00 208 V Z =12+ i 9 Z + Vbn=120 -1200 _ 0. 06 Figure 1 i 0. 12

Solution 3. 8 (a)The magnitude of the line current IL So, the magnitude of the line current is thus 7. 94 A

(b) The magnitude of the load’s line and phase voltages VLL and V L The phase voltage on the load is the voltage across one phase of the load. This voltage is the product of the phase impedance and the phase current of the load Therefore, the magnitude of the load’s phase voltage is and the magnitude of the load’s line voltage is

(c) The real power consumed by the load is The reactive power consumed by the load is The apparent power consumed by the load is

(d) The load power factor is (e) The current in the transmission line is The impedance per phase of the line is or Therefore, the real, reactive and apparent powers consumed in the line are

(f) The real and reactive powers supplied by the generator are the sum of the powers consumed by the line and the load The apparent power of the generator is the square root of the sum of the squares of the real and reactive powers

(g) From the power triangle, the power factor angle is Therefore, the generator’s power factor is

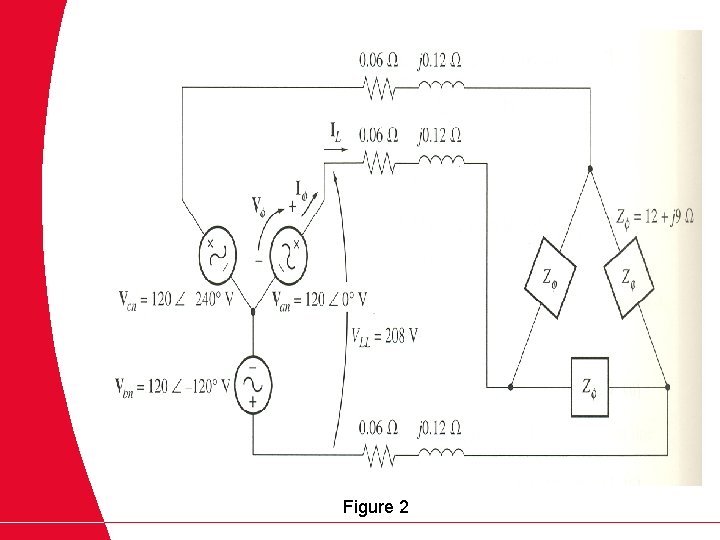
A 208 V three phase power system is shown in Figure 2. It consists of an ideal 208 V Y - connected three phase generator connected to a three phase transmission line to a - connected load. The transmission line has an impedance of 0. 06 + j 0. 12 W per phase and the load has an impedance of 12 + j 9 W per phase. For this simple system, find a. The magnitude of the line current IL Assignment 3. 1 b. The magnitude of the load’s line and phase voltages VLL and V L c. The real, reactive and apparent powers consumed by the load d. The power factor of the load e. The real, reactive and apparent powers consumed by the transmission line f. The real, reactive and apparent powers supplied by the generator g. The generator’s power factor

Figure 2