3 1 Image and Kernel Null Space This

3. 1 Image and Kernel (Null Space) This is an image of the cloud around a black hole from the Hubble Telescope

Image of a Function for more information on image and codomain visit: http: //en. wikipedia. org/wiki/Codomain The image of a function consists of all of the values that the function takes in its codomain.

Our book offers this anecdote to explain domain codomain and image A group of X students and a group of Y professors stand in the yard. Each student throws a tomato at one of the professors (and each tomato hits intended target). Consider the function y = f(x) from X to Y that associates each x with a y. X is the domain, Y is the codomain and the professors that actually get hit by a tomato are the image

Consider a 2 x 3 matrix a 11 a 12 a 13 a 21 a 22 a 23 This matrix represents a mapping from R 3 to R 2 R 3 is the domain R 2 is the codomain The image is the set of points in R 2 that can result from multiplying Ax = b

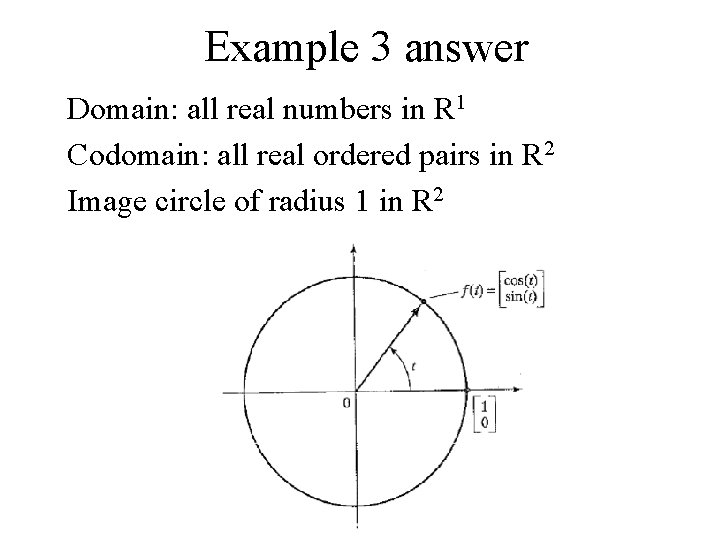
Example 3 Find the Domain, Codomain and Image of the function

Example 3 answer Domain: all real numbers in R 1 Codomain: all real ordered pairs in R 2 Image circle of radius 1 in R 2

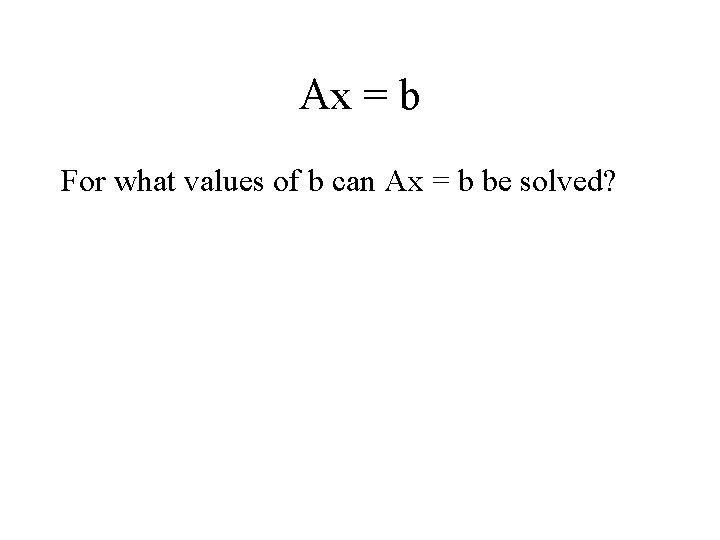
Ax = b For what values of b can Ax = b be solved?

Ax = b For what values of b can Ax = b be solved? We can solve Ax = b when b is a linear combination of the columns of A. Why is this true? We call the region that is comprised of all of the linear combinations of the columns of the image or column space of matrix A.

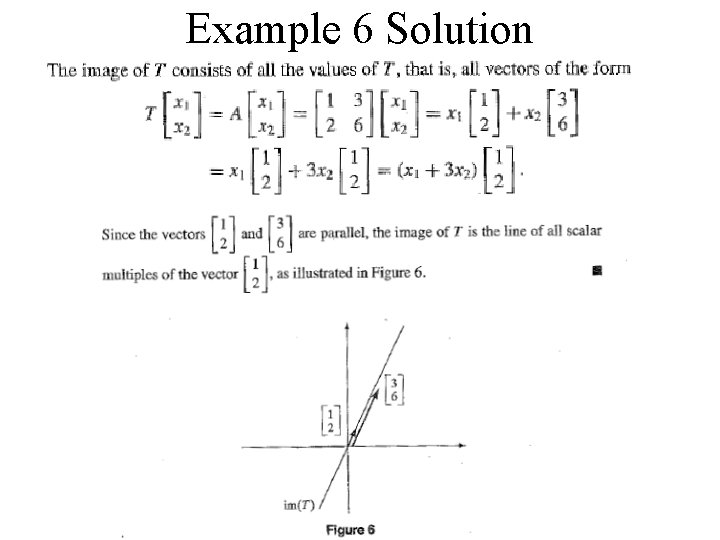
Example 6

Example 6 Solution

Span Consider a set of vectors. The set of all linear combinations of these vectors is called their span.

How do we describe the image of A? Find all of the columns that are independent. There are 3 ways this is generally done. 1) If the matrix is simple do by inspection. (use number sense to determine which columns are independent shown on a later slide – we will practice this in 3. 2) Put the matrix in reduced row echelon form. Every column that has a leading one in this form is independent. The columns (in the un-simplified form) form a basis for the image. 3) We can use our knowledge of our library of basic matrices to describe the image and kernel of A (We will practice this method tomorrow).

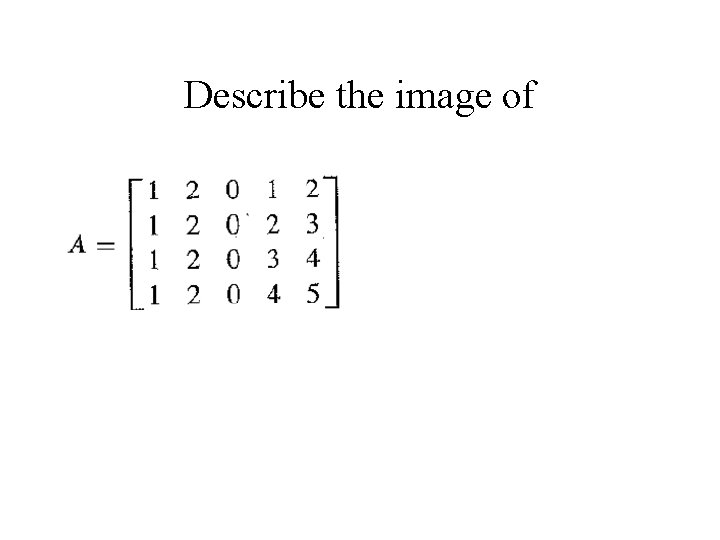
Describe the image of

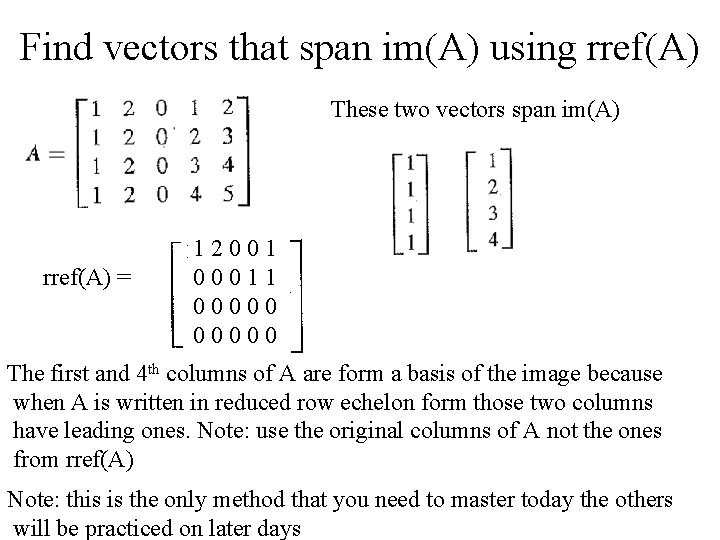
Find vectors that span im(A) using rref(A) These two vectors span im(A) rref(A) = 12001 00011 00000 The first and 4 th columns of A are form a basis of the image because when A is written in reduced row echelon form those two columns have leading ones. Note: use the original columns of A not the ones from rref(A) Note: this is the only method that you need to master today the others will be practiced on later days

Find the basis of the image by inspection Answer: columns 1 and 4 form a basis of the image We will practice this in 3. 2 and 3. 3 Consider the columns 1) The first column is in the basis for the image because it is non-zero 2) The second column is not in the basis for the image because it is a multiple of column 1 3) The third column is not in the basis because it is the zero vector 4) The fourth column is in the basis because it is not a multiple of column 1 (the only vector that is in our basis so far) 5) The 5 th column is not in the basis because it is the sum of column 1 and 4

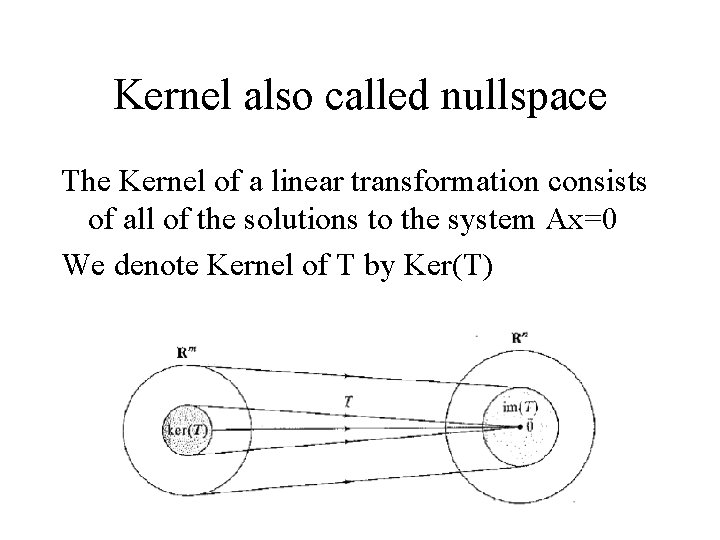
Kernel also called nullspace The Kernel of a linear transformation consists of all of the solutions to the system Ax=0 We denote Kernel of T by Ker(T)

Describe the kernel of

Find vectors that span the kernel of A Set Ax = 0 Solve and find all solutions Find rref(A) x 1 = -2 r –t x 2 = r x 3 = s r x 4 = -t x 5 = t 12001 00011 00000 -2 1 0 0 0 +s x 2, x 3 and x 5 are free variables Set x 2 = r, x 3 = s, x 5 = t 0 0 1 0 0 -1 0 +t 0 -1 1 The three column vectors are a basis for the kernel How can you check?

Problem 2 Find vectors that Span the Kernel of the following matrix

Problem 2 Solution

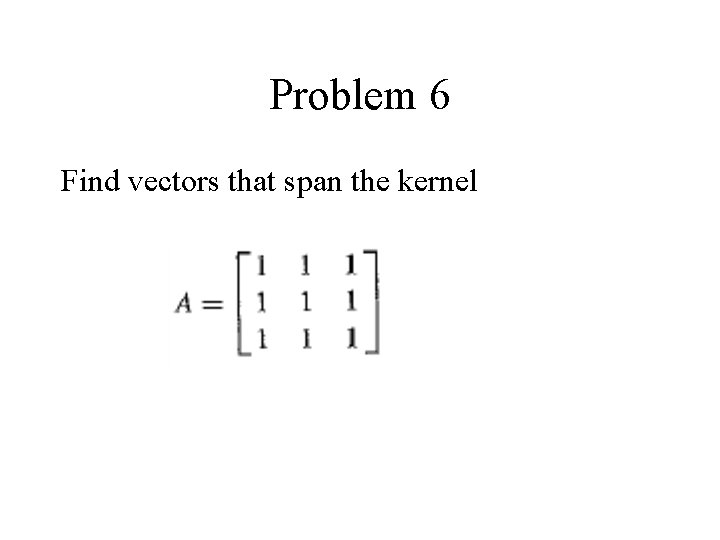
Problem 6 Find vectors that span the kernel

Problem 6 solution

Homework p. 110 1 -21 odd Black holes are where God divided by zero. Practice is not always easy… but if you hang in there you’ll get it.