2005 11 15 Homework Homework due now Reading

2005 11 15 Homework • Homework due now. • Reading: relations

Counting, Using Permutations and Combinations PC 13. In a competition among architects on emergency housing, a panel votes on the four top designs (labeled poptop, cocoon, box, and dome). How many outcomes are possible? (You must consider ties, including multi-way ties. ) Without ties, it’s P(4, 4) With ties, there are five cases: Select Order 1) No ties: P(4, 4) 2) Two tie, other two don’t: C(4, 2) * P(3, 3) 3) Two sets of two tie: C(4, 2) 4) Three houses tie: C(4, 3) * P(2, 2) 5) Four houses tie: 1 +

Binomial Coefficients

Pascal’s Triangle

Chu Shih-chieh’s Triangle?

Binomial Coefficients Theorem:

Binomial Coefficients BC 1. Find the coefficients for the following terms a. the fifth term of (2 x + 3 y)7 b. the coefficient of x 4 y 7 in (x + y)11 c. the coefficient of a 62 b 92 in (2 a – b)154 C(11, 4) or 11 4 ( )

Binomial Coefficients BC 6. Show that if p is a prime and k is an integer p such that 1 k p-1 then p divides ( k ).

Binomial Coefficients BC 10. Prove that in any row of Pascal’s triangle, the sum of the entries in the odd numbered positions equals the sum of the entries in the even numbered positions.

Beware! Coincidences Often Aren’t; The Obvious Often Isn’t. How many people must be in a room to make it likely two or more of them have the same birthday? 385 How many people must be in a room to make it likely at least one of them has the same birthday you do? 183 Monty Hall: N (>2) doors, one has what you want behind it. You choose a door. Before opening it, Monty opens one you didn’t choose to reveal it’s not the one you want. Now, should you stay with the door you selected, or switch? Or doesn’t it matter? Doesn’t matter

Discrete Probability • p(E) = |E| / |S| – Events, E, equally likely; sample space, S, finite. • If two dice are rolled once, what is the probability their sum is odd? – (Outcomes: 2, 4, 6, 8, 10, 12; 3, 5, 7, 9, 11) • Using counting technique to find probabilities – Problem DP 11 demonstrates well • # of 5 -card hands that have four of the same kind • # of 5 -card hands that are a full house • Thm: p(E) = 1 - p(E) • Thm: p(E 1 E 2) = p(E 1) + p(E 2) – p(E 1 E 2)

Sum of Two Dice If two dice are rolled once, what is the probability their sum is odd? (Since the smallest sum is two and the largest is twelve, perhaps there are more even sums? ) Odd: (1, 2), (1, 4), (1, 6), (2, 1), (2, 3), (2, 5), (3, 2), (3, 4), (3, 6), (4, 1), (4, 3), (4, 5), (5, 2), (5, 4), (5, 6), (6, 1), (6, 3), (6, 5) Even: (1, 1), (1, 3), (1, 5), (2, 2), (2, 4), (2, 6), (3, 1), (3, 3), (3, 5), (4, 2), (4, 4), (4, 6), (5, 1), (5, 3), (5, 5), (6, 2), (6, 4), (6, 6) p(E) = |E| / |S| = 18 / (18 + 18) = 1/2

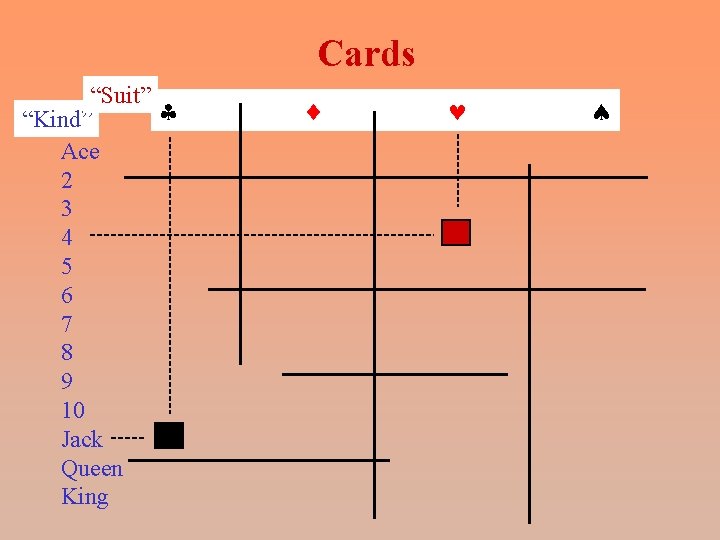
Cards “Suit” § “Kind” Ace 2 3 4 5 6 7 8 9 10 Jack Queen King ¨ © ª

Discrete Probability DP 7. What is the probability that a card dealt from the deck is a. a spade or a heart? b. a face card? c. a jack or a spade? 16 cards satisfy: “jack or spade”, so probability is: C(16, 1) / C(52, 1) Alternatively. 4/52 + 13/52 – 1/52

Discrete Probability DP 8. Assume you are dealt a 13 card hand. What is the probability that you have a. the ace of spades? b. at least two aces? c. exactly two aces? There are C(4, 2) ways to choose the two aces. The number of ways to choose the remaining three cards from 48 is C(48, 3), so the probability is: C(4, 2) C(48, 3) / C(52, 5) where C(52, 5) is the number of all five card hands.

Flush DP 11. Compute the probability of each of the following types of poker hands: a. flush The number of ways to create a flush is: C(4, 1) * C(13, 5) So the requested probability is: C(4, 1) * C(13, 5) / C(52, 5)

Flush – an alluring incorrect answer DP 11. Compute the probability of each of the following types of poker hands: a. flush What about: C(52, 1) * C(12, 4) / C(52, 5) ? ? ? Choose 4 more to match its suit Choose a first card Answer is off by a factor equal to the number of cards in the hand. Why?

Five Card Hand with Four Same Rank DP 11. Compute the probability of each of the following types of poker hands: d. 4 of a kind Choose a kind: C(13, 1) Choose four out of four of a kind: C(4, 4) Any fifth card: C(48, 1) Number of possible five card hands: C(52, 5) Desired probability: C(13, 1) * C(4, 4) * C(48, 1) ~ 0. 00024 C(52, 5)

Full House DP 11. Compute the probability of each of the following types of poker hands: f. full house (3 of a kind + one pair) Arrange 2 out of 13 kinds: P(13, 2) Choose 3 out of four of the first kind: C(4, 3) Choose 2 out of four of second kind: C(4, 2) Desired probability: P(13, 2) * C(4, 3) * C(4, 2) ~ 0. 0014 C(52, 5)

Lottery DP 15. To play the Big Bang lottery, the contestant guesses 7 numbers out of the integers from 1 to 77, no repetitions allowed. To win, the set of guessed numbers must be a subset of the 12 integers from the same range drawn by a lottery official. (Assume on each draw, any number in the range has an equal probability of being selected. ) a. What is the probability that a contestant who plays once wins the Big Bang lottery? Number of ways to select 7 of 12 numbers: C(12, 7) divided by number of ways to select 7: - OR C(77, 7) Number of ways for lottery to select 12 when drawing our 7: C(70, 5) divided by number of ways to select 12:

Defining Independence Two events, E 1 and E 2, are called independent if p(E 1 E 2) = p(E 1) * p(E 2). It’s very important to know whether two events are independent. - If events are treated as independent, and they’re not, it can seriously degrade the quality of any analysis that assumes they are. Analysis in which events can be assumed independent is often simplified considerably.

Evaluating Independence DP 18. Let E 1, E 2, … En be events in the sample space S. For each of the following propositions, restate it in English, say whether it is true or false, and give an argument supporting your answer. a. E 1 E 2 P(E 1) P(E 2) b. P(E 1 E 1) = 1 c. If E 1, E 2, and E 3 are independent events, then P(E 1 E 2 E 3) = P(E 1) P(E 2) P(E 3). d. P(E 1 E 2) = P(E 1) + P(E 2) e. P(E 1 E 2) P(E 1) + P(E 2) E 1 E 2 P(E 1) P(E 2) TRUE. Why? E 1 E 2 |E 1| |E 2| |E 1| / |S| |E 2| / |S| P(E 1) P(E 2)

Evaluating Independence DP 18. Let E 1, E 2, … En be events in the sample space S. For each of the following propositions, restate it in English, say whether it is true or false, and give an argument supporting your answer. a. E 1 E 2 P(E 1) P(E 2) b. P(E 1 E 1) = 1 c. If E 1, E 2, and E 3 are independent events, then P(E 1 E 2 E 3) = P(E 1) P(E 2) P(E 3). d. P(E 1 E 2) = P(E 1) + P(E 2) e. P(E 1 E 2) P(E 1) + P(E 2) TRUE. |E 1 E 2| |E 1| + |E 2| |E 1 E 2| / |S| |E 1| / |S| + |E 2| / |S| P(E 1 E 2) P(E 1) + P(E 2) Why? by def of

In a room with 82 people in it, what are the odds two or more of them have the same birthday?

In a room with 82 people in it, what are the odds one of them has the same birthday you do? - different question! Look here

? ? ? Stick, or switch? X

Monty Hall with N Doors DP 17. Generalize the Monty Hall problem to n ³ 4 doors. After you’ve selected a door and Monty opens one with a valueless prize behind it, should you switch doors if offered the opportunity? Compute the probability that you win if you stick with your original choice and the probability that you win if you switch to another unopened door. ¼ chance of winning initially, and if you do not change. Thus, ¾ chance it’s one of the other doors. Since there are only two equally likely choices, chances if you change are 3/8.

Beware! Coincidences Often Aren’t; The obvious often isn’t. How many people must be in a room to make it likely two or more of them have the same birthday? 385 How many people must be in a room to make it likely at least one of them has the same birthday you do? 183 Monty Hall: N (>2) doors, one has what you want behind it. You choose a door. Before opening it, Monty opens one you didn’t choose to reveal it’s not the one you want. Now, should you stay with the door you selected, or switch? Or doesn’t it matter? Doesn’t matter

An Empirical Test of Our Theory Everybody write down a number: 1, 2, or 3 Loop until my point is made Student a: Tell us your number (pick a door) Student b: Tell us a number that is not the number “a” chose, and not the number you wrote down (open a door that is not the one “a” selected and not the one with the prize) Student a: Pick the remaining number (switch!) Student b: Is this the number you wrote down? off yes -> switching paid off no -> didn’t pay

Transition

Match Some DP 16. Consider a lottery in which the contestant selects 6 numbers from among 40 possible, and 6 numbers are also chosen randomly by the state. What is the probability that exactly 5 (i. e. not 6) of the numbers chosen by the contestant match 5 of the 6 chosen by the state? Ways to select 5 out of 6: C(6, 5) Ways to select remaining number: * C(34, 1) divided by number of ways to select 6: C(40, 6)