2 Cartesian Vectors 1 RightHanded Coordinate System A

2

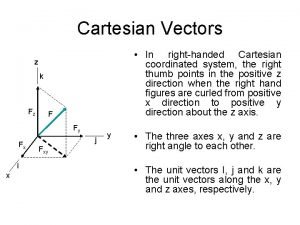
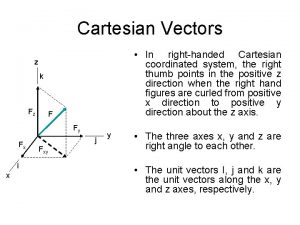
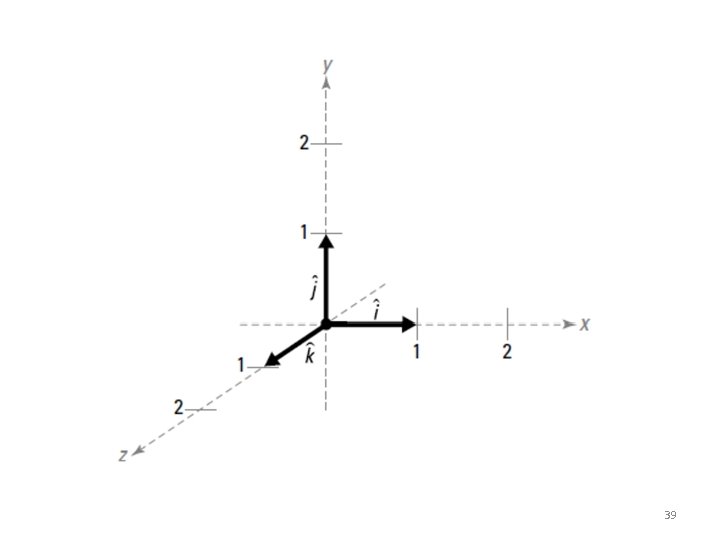
Cartesian Vectors (1) • Right-Handed Coordinate System A rectangular or Cartesian coordinate system is said to be right-handed provided: - Thumb of right hand points in the direction of the positive z axis when the right-hand fingers are curled about this axis and directed from the positive x towards the positive y axis 3

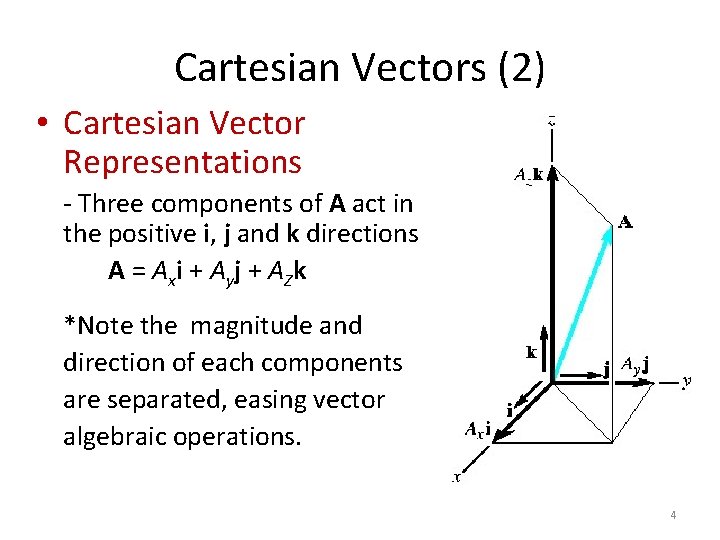
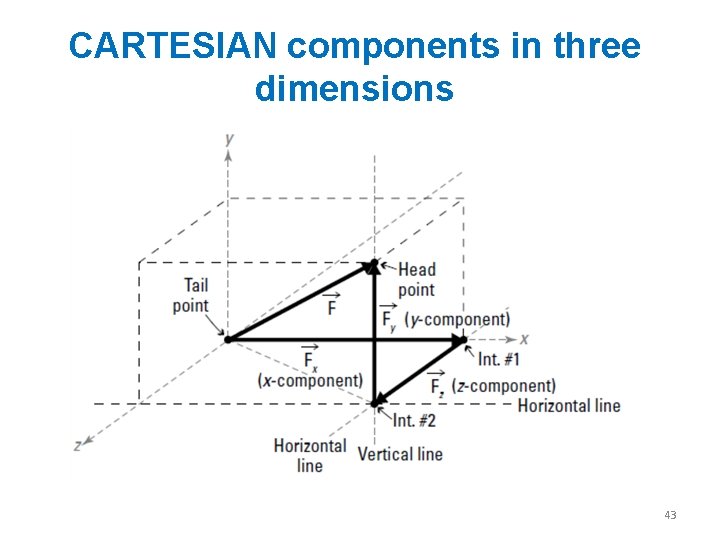
Cartesian Vectors (2) • Cartesian Vector Representations - Three components of A act in the positive i, j and k directions A = A xi + A y j + A Z k *Note the magnitude and direction of each components are separated, easing vector algebraic operations. 4

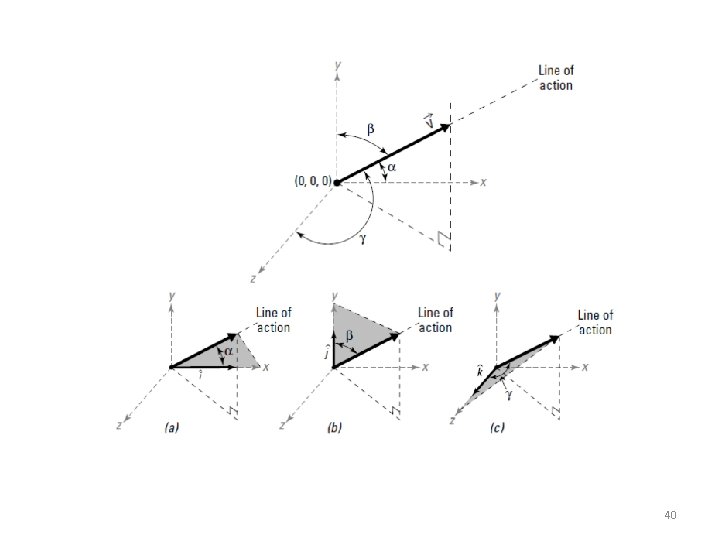
Cartesian Vectors (3) • Direction of a Cartesian Vector - Orientation of A is defined as the coordinate direction angles α, β and γ measured between the tail of A and the positive x, y and z axes - 0° ≤ α, β and γ ≤ 180 °

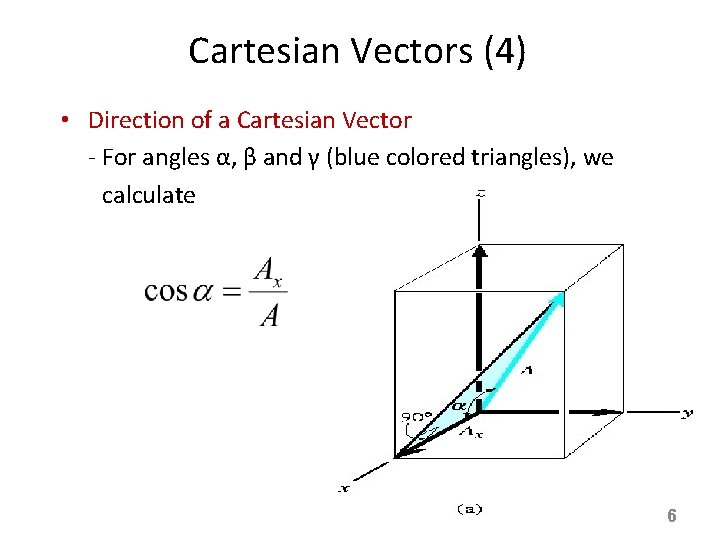
Cartesian Vectors (4) • Direction of a Cartesian Vector - For angles α, β and γ (blue colored triangles), we calculate the direction cosines of A 6

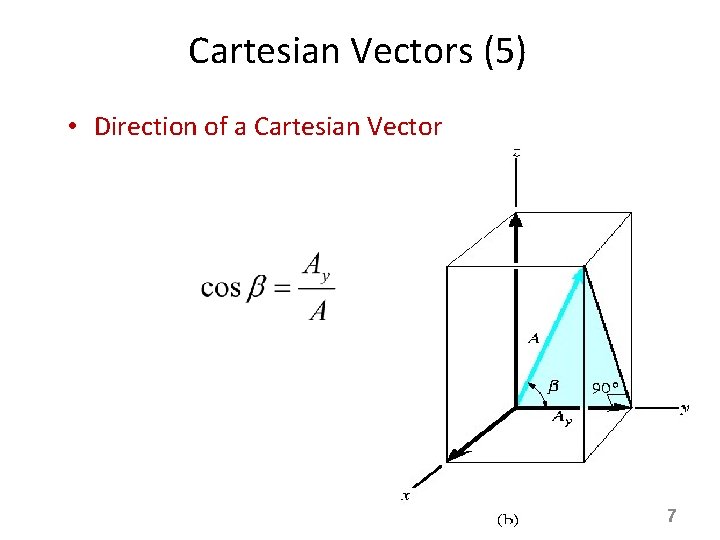
Cartesian Vectors (5) • Direction of a Cartesian Vector - For angles α, β and γ (blue colored triangles), we calculate the direction cosines of A 7

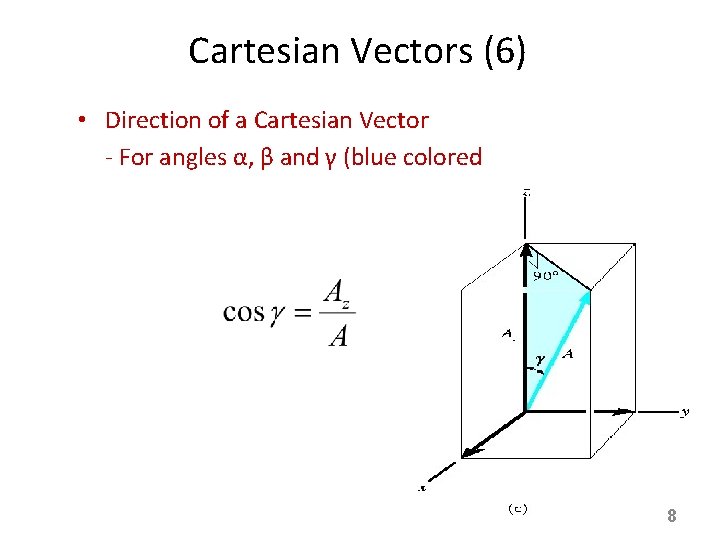
Cartesian Vectors (6) • Direction of a Cartesian Vector - For angles α, β and γ (blue colored triangles), we calculate the direction cosines of A 8

Cartesian Vectors (7) • Direction of a Cartesian Vector - Angles α, β and γ can be determined by the inverse cosines - Given Then, A = A xi + A y j + A Z k u. A = A /A = (Ax/A)i + (Ay/A)j + (AZ/A)k where 9

Cartesian Vectors (8) • Direction of a Cartesian Vector - u. A can also be expressed as u. A = cosαi + cosβj + cosγk - Since and magnitude of u. A = 1, A as expressed in Cartesian vector form A = Au. A = Acosαi + Acosβj + Acosγk = A xi + A y j + A Z k 10

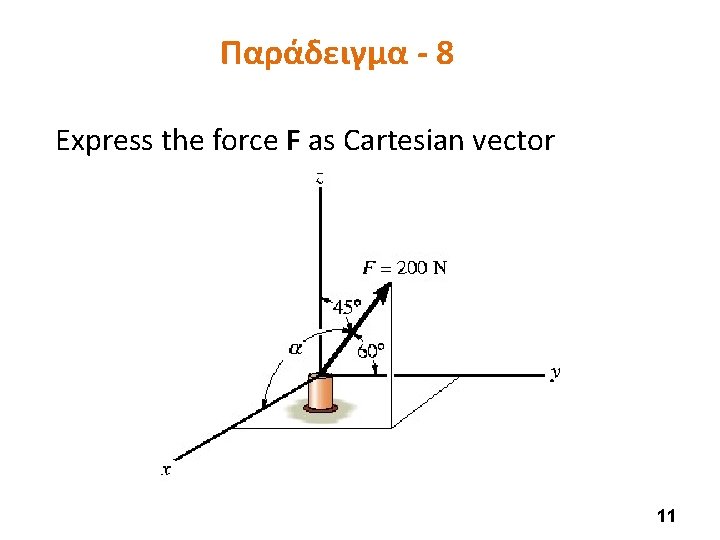
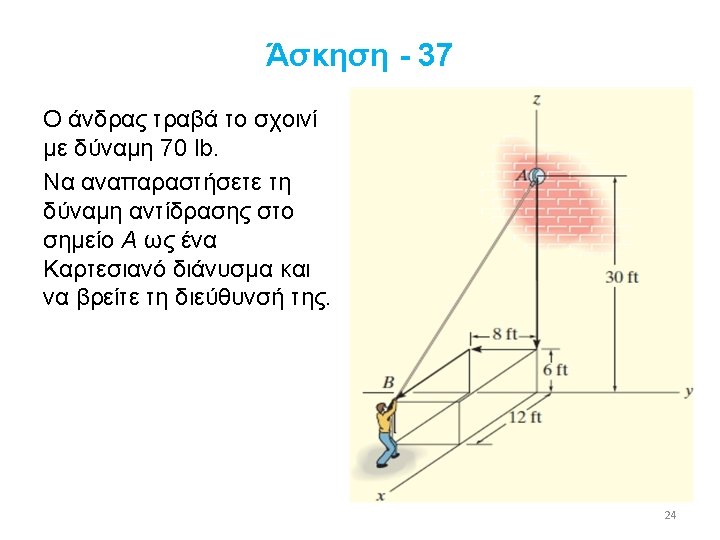
Παράδειγμα - 8 Express the force F as Cartesian vector 11

Λύση (1) Since two angles are specified, the third angle is found by Two possibilities exit, namely or 12

Λύση (2) By inspection, α = 60° since Fx is in the +x direction Given F = 200 N F = Fcosαi + Fcosβj + Fcosγk = (200 cos 60°N)i + (200 cos 60°N)j + (200 cos 45°N)k = {100. 0 i + 100. 0 j + 141. 4 k}N Checking: 13

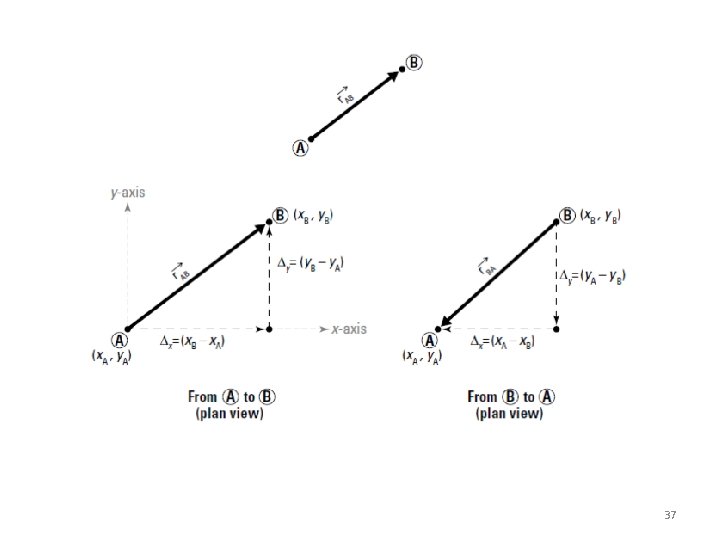
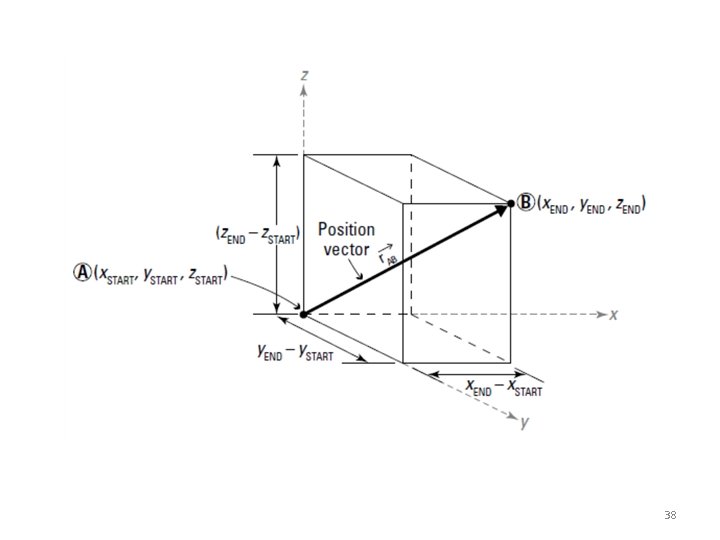
Rectangular Components in Space • The vector is contained in the plane OBAC. • Resolve into horizontal and vertical components. • Resolve into rectangular components 14

Rectangular Components in Space • With the angles between • and the axes, is a unit vector along the line of action of are the direction cosines for 15

Rectangular Components in Space Direction of the force is defined by the location of two points, 16

3. Collect and equate components. For the components: (1) For the components: (2) Now, what? COUNT EQUATIONS AND UNKNOWNS!!!!!!! Two equations, (1) and (2), and two unknowns, F and 18 .

From (1) and (2), (3) (4) Now, what? For the angle, divide (4) by (3) to get For the magnitude, 19

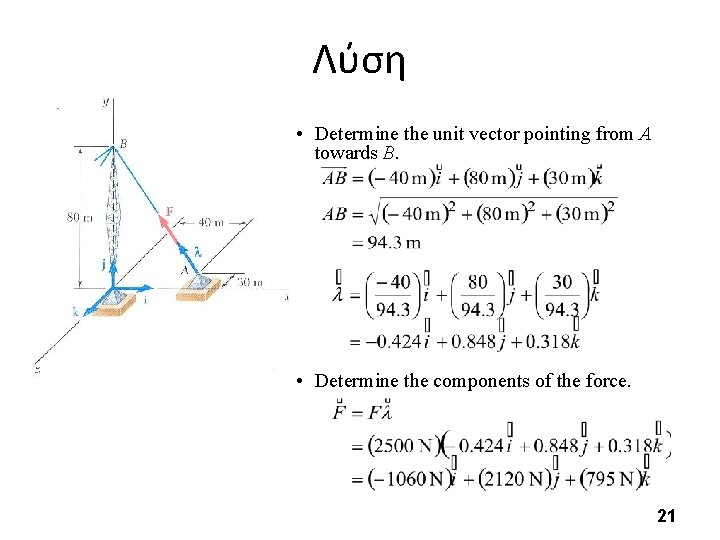
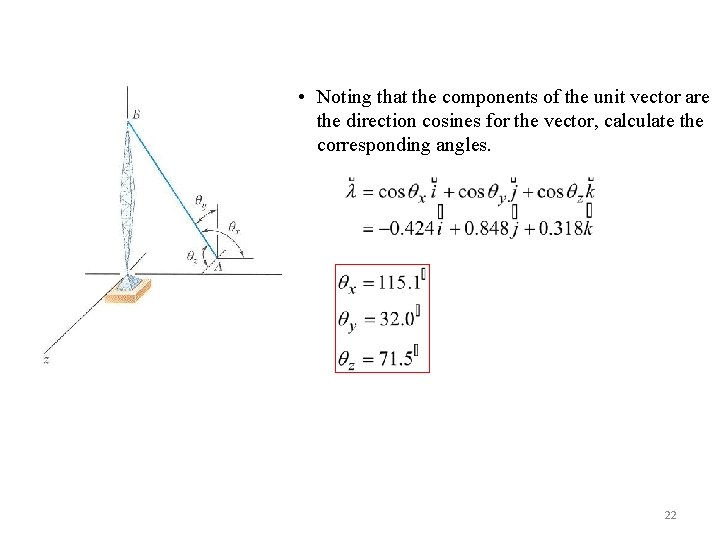
Παράδειγμα - 10 STEPS : • Based on the relative locations of the points A and B, determine the unit vector pointing from A towards B. • Apply the unit vector to determine the components of the force acting on A. The tension in the guy wire is 2500 N. Determine: • Noting that the components of the unit vector are the direction cosines for the vector, calculate the corresponding angles. a) components Fx, Fy, Fz of the force acting on the bolt at A, b) the angles qx, qy , qz defining the direction of the force 20

Λύση • Determine the unit vector pointing from A towards B. • Determine the components of the force. 21

• Noting that the components of the unit vector are the direction cosines for the vector, calculate the corresponding angles. 22

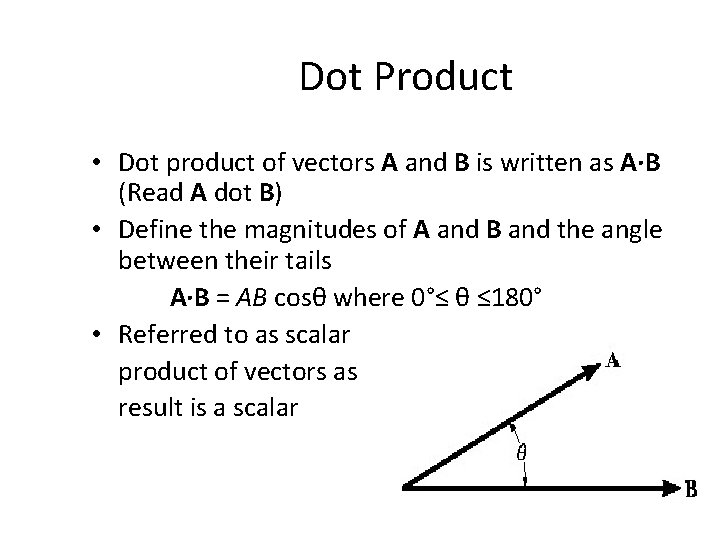
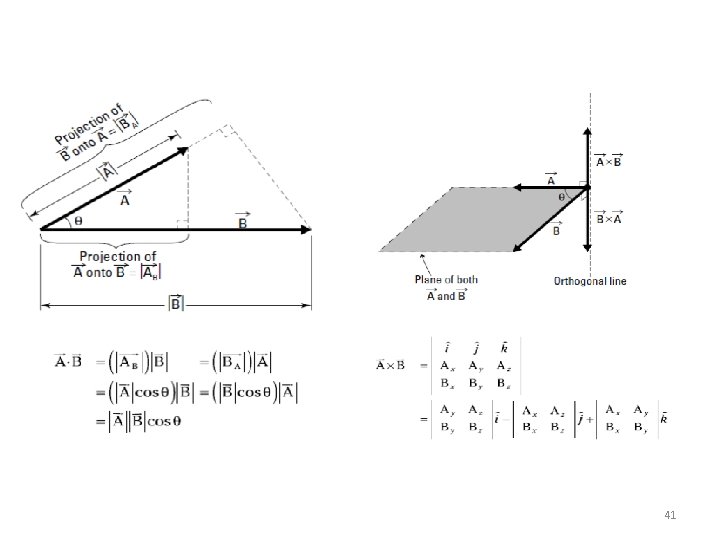
Dot Product • Dot product of vectors A and B is written as A·B (Read A dot B) • Define the magnitudes of A and B and the angle between their tails A·B = AB cosθ where 0°≤ θ ≤ 180° • Referred to as scalar product of vectors as result is a scalar

Dot Product Laws of Operation 1. Commutative law A·B = B·A 2. Multiplication by a scalar a(A·B) = (a. A)·B = A·(a. B) = (A·B)a 3. Distribution law A·(B + D) = (A·B) + (A·D)

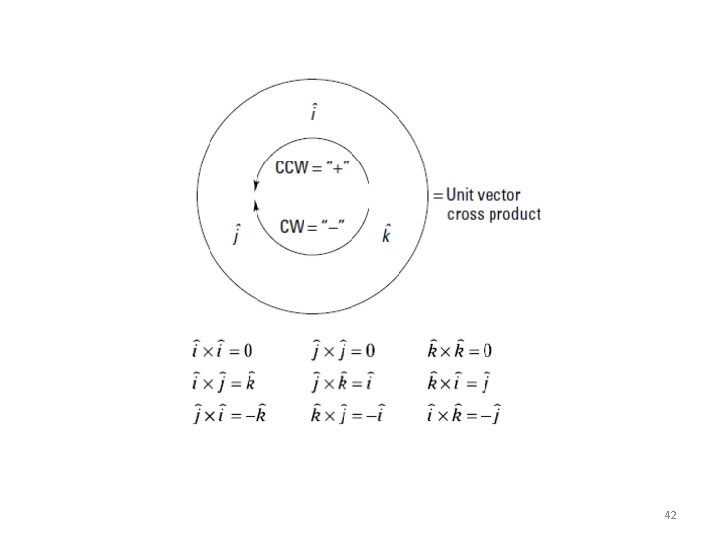
Dot Product Cartesian Vector Formulation - Dot product of Cartesian unit vectors Eg: i·i = (1)(1)cos 0° = 1 and i·j = (1)(1)cos 90° = 0 - Similarly i·i = 1 j·j = 1 k·k = 1 i·j = 0 i·k = 0 j·k = 0

Dot Product • Cartesian Vector Formulation - Dot product of 2 vectors A and B A·B = (Axi + Ayj + Azk)· (Bxi + Byj + Bzk) = Ax. Bx(i·i) + Ax. By(i·j) + Ax. Bz(i·k) + Ay. Bx(j·i) + Ay. By(j·j) + Ay. Bz(j·k) + Az. Bx(k·i) + Az. By(k·j) + Az. Bz(k·k) = A x B x + A y B y + A z. B z Note: since result is a scalar, be careful of including any unit vectors in the result

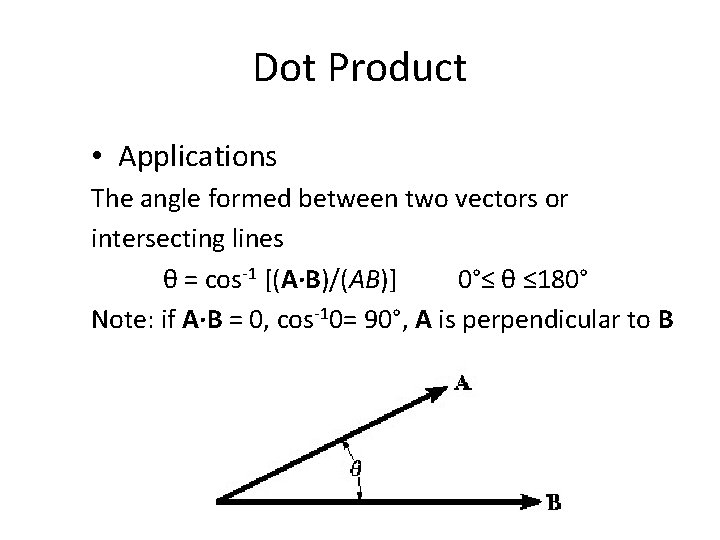
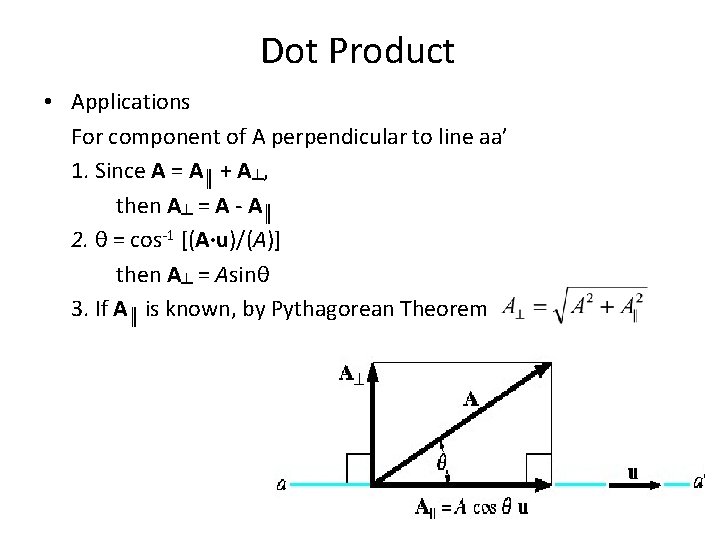
Dot Product • Applications The angle formed between two vectors or intersecting lines θ = cos-1 [(A·B)/(AB)] 0°≤ θ ≤ 180° Note: if A·B = 0, cos-10= 90°, A is perpendicular to B

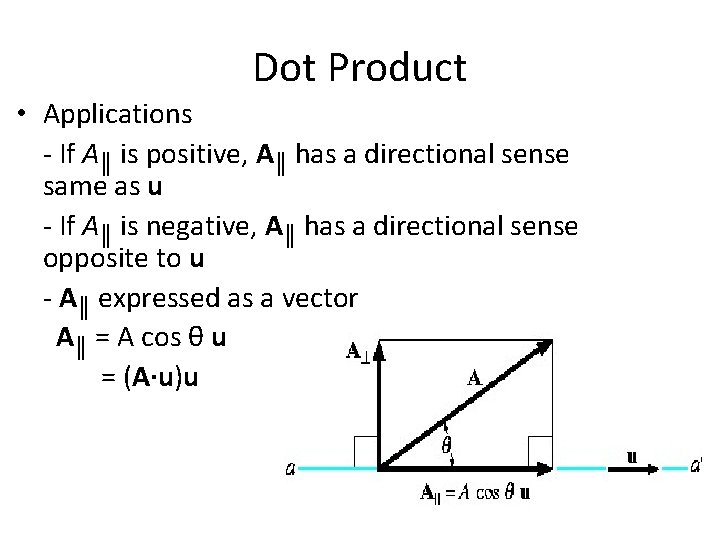
Dot Product • Applications - If A║ is positive, A║ has a directional sense same as u - If A║ is negative, A║ has a directional sense opposite to u - A║ expressed as a vector A║ = A cos θ u = (A·u)u

Dot Product • Applications For component of A perpendicular to line aa’ 1. Since A = A║ + A┴, then A┴ = A - A║ 2. θ = cos-1 [(A·u)/(A)] then A┴ = Asinθ 3. If A║ is known, by Pythagorean Theorem

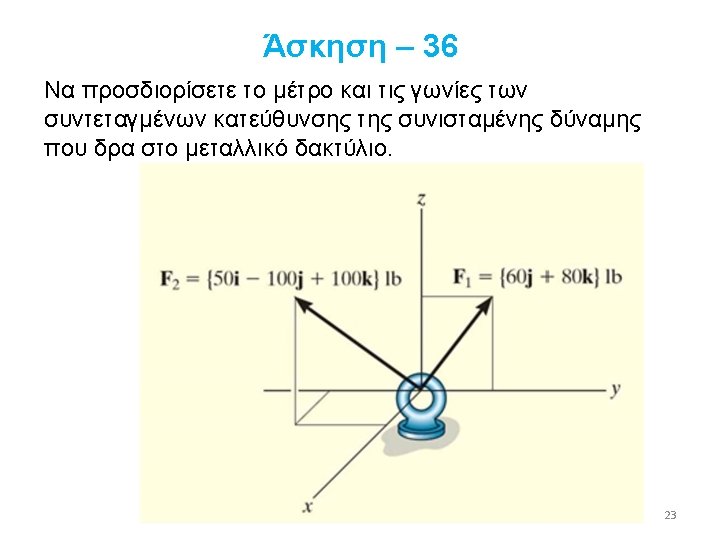
35

36

37

38

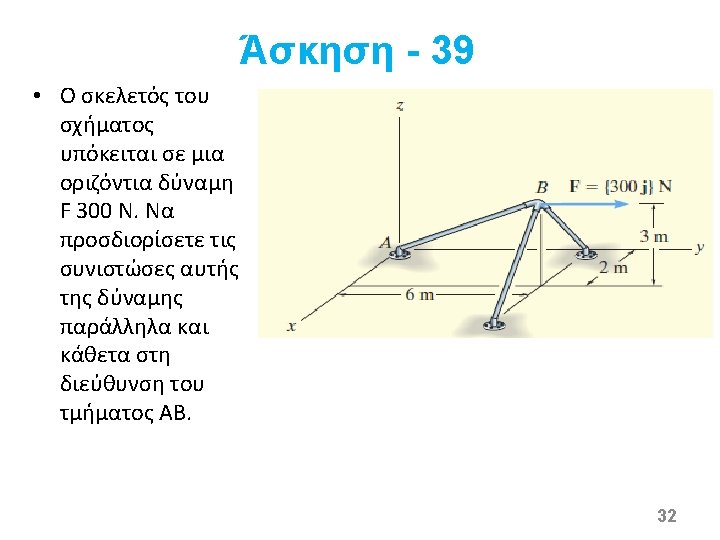
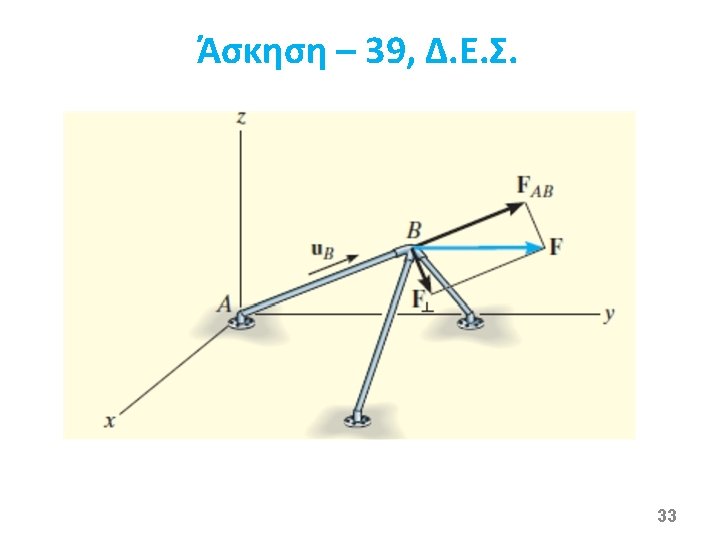
39

40

41

42

CARTESIAN components in three dimensions 43