Chapter 2 Force Vectors Engineering Mechanics Statics Mohammad






















































![2. 7 Position Vectors Solution Position vector r = [-2 m – 1 m]i 2. 7 Position Vectors Solution Position vector r = [-2 m – 1 m]i](https://slidetodoc.com/presentation_image_h/a31871047fd57c2dacb9f552ccda5c25/image-69.jpg)











- Slides: 81

Chapter 2: Force Vectors Engineering Mechanics: Statics Mohammad Shahril bin Salim 2012/2013

Objectives • To show to add forces and resolve them into components using the Parallelogram Law. • To express force and position in Cartesian vector form and explain how to determine the vector’s magnitude and direction. • To introduce the dot product in order to determine the angle between two vectors or the projection of one vector onto another.

Chapter Outline • • • Scalars and Vectors Vector Operations Vector Addition of Forces Addition of a System of Coplanar Forces Cartesian Vectors

Chapter Outline • Addition and Subtraction of Cartesian Vectors • Position Vectors • Force Vector Directed along a Line • Dot Product

2. 1 Scalars and Vectors • Scalar – A quantity characterized by a positive or negative number that can be specified by its magnitude. Eg: Mass, volume and length

2. 1 Scalars and Vectors • Vector – A quantity that has both magnitude and direction Eg: Position, force and moment – Represent by a letter with an arrow over it such as – Magnitude is designated as or simply A – In this subject, vector is presented as A and its magnitude (positive quantity) as A

Scalars and Vectors Vector – Represented graphically as an arrow – Length of arrow = Magnitude of Vector – Angle between the reference axis and arrow’s line of action = Direction of Vector – Arrowhead = Sense of Vector

2. 2 Vector Operations Vector Addition - Addition of two vectors A and B gives a resultant vector R by the parallelogram law - Resultant vector, R can be found by triangle construction - Communicative Eg: R = A + B = B + A

2. 2 Vector Operations

2. 2 Vector Operations Vector Subtraction - Special case of addition Eg: R’ = A – B = A + ( - B ) - Rules of Vector Addition Applies

2. 3 Vector Addition Forces • When two or more forces are added, successive applications of the parallelogram law is carried out to find the resultant Example Forces F 1, F 2 and F 3 acts at a point O a) First, find resultant of F 1 + F 2 Solution; Resultant, • FR = ( F 1 + F 2 ) + F 3

Procedure of Analysis a) Parallelogram Law b) Trigonometry

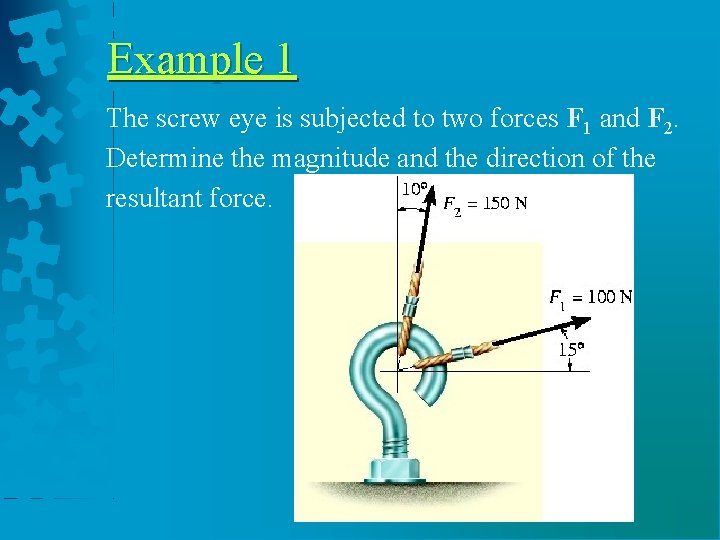
Example 1 The screw eye is subjected to two forces F 1 and F 2. Determine the magnitude and the direction of the resultant force.

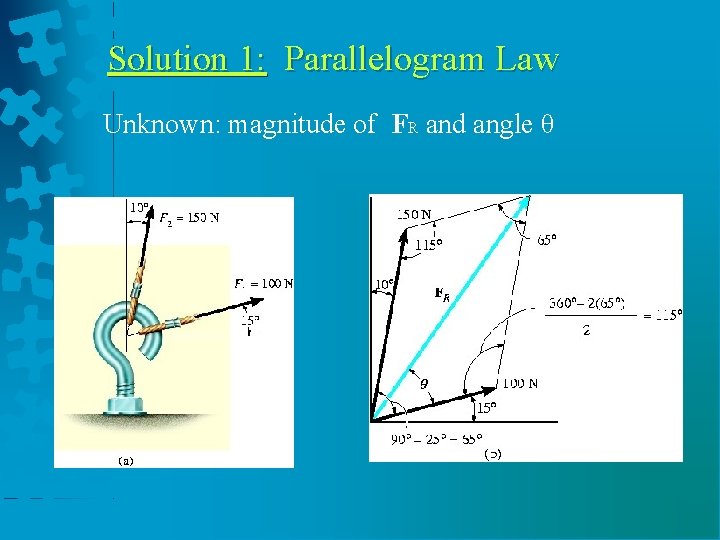
Solution 1: Parallelogram Law Unknown: magnitude of FR and angle θ

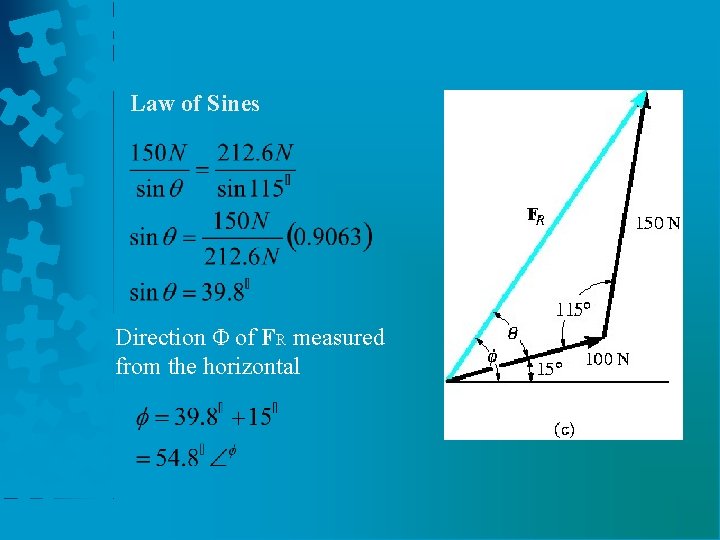
Solution 2: Trigonometry Law of Cosines

Law of Sines Direction Φ of FR measured from the horizontal

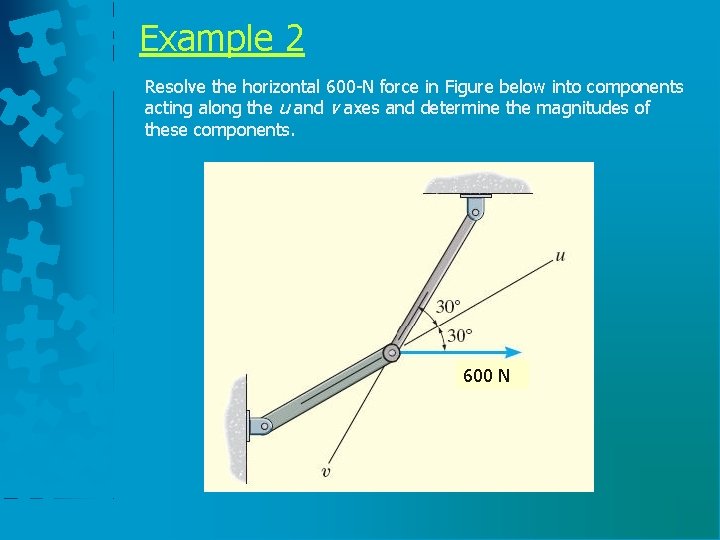
Example 2 Resolve the horizontal 600 -N force in Figure below into components acting along the u and v axes and determine the magnitudes of these components. 600 N

600 N N N 600 N

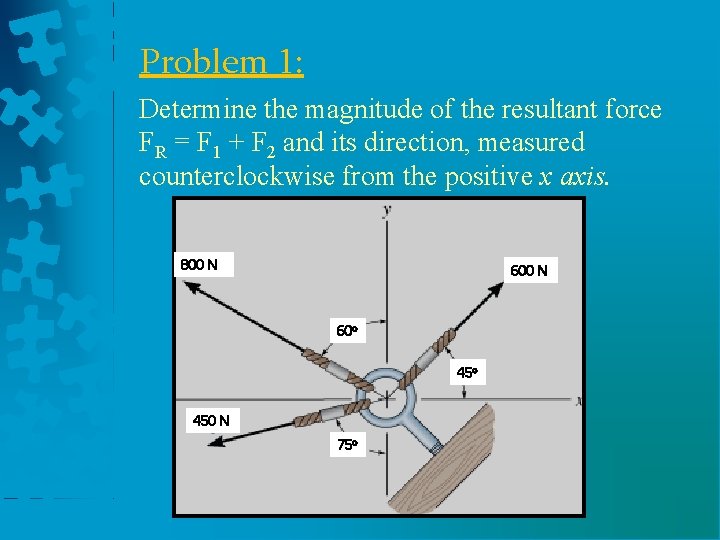
Problem 1: Determine the magnitude of the resultant force FR = F 1 + F 2 and its direction, measured counterclockwise from the positive x axis. 800 N 60 o 450 N 75 o

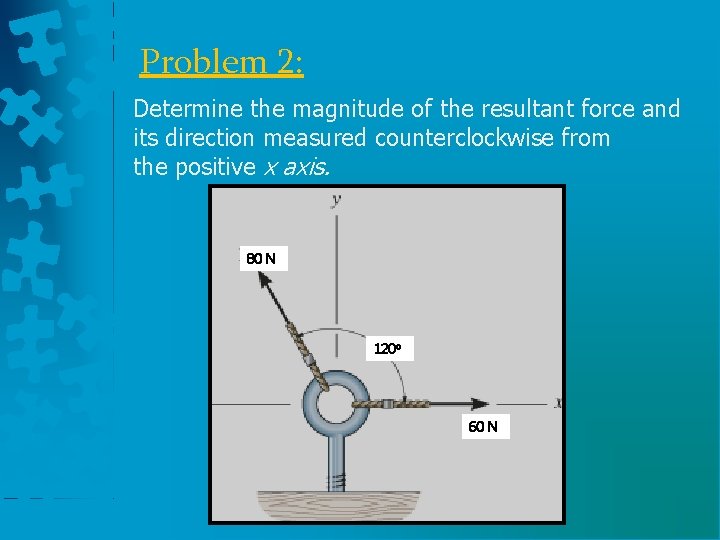
Problem 2: Determine the magnitude of the resultant force and its direction measured counterclockwise from the positive x axis. 80 N 120 o 60 N

Problem 3: Determine the magnitude of the resultant force FR = F 1 + F 2 and its direction, measured counterclockwise from the positive u axis. 70 o 30 o 45 o 500 N 300 N

2. 4 Addition of a System of Coplanar Forces For resultant of two or more forces: • Find the components of the forces in the specified axes • Add them algebraically • Form the resultant In this subject, we resolve each force into rectangular forces along the x and y axes.

2. 4 Addition of a System of Coplanar Forces • Scalar Notation - x and y axes are designated positive and negative - Components of forces expressed as algebraic scalars Eg: Sense of direction along positive x and y axes

2. 4 Addition of a System of Coplanar Forces • Scalar Notation - Head of a vector arrow = sense of the vector graphically (algebraic signs not used) - Vectors are designated using boldface notations - Magnitudes (always a positive quantity) are designated using italic symbols

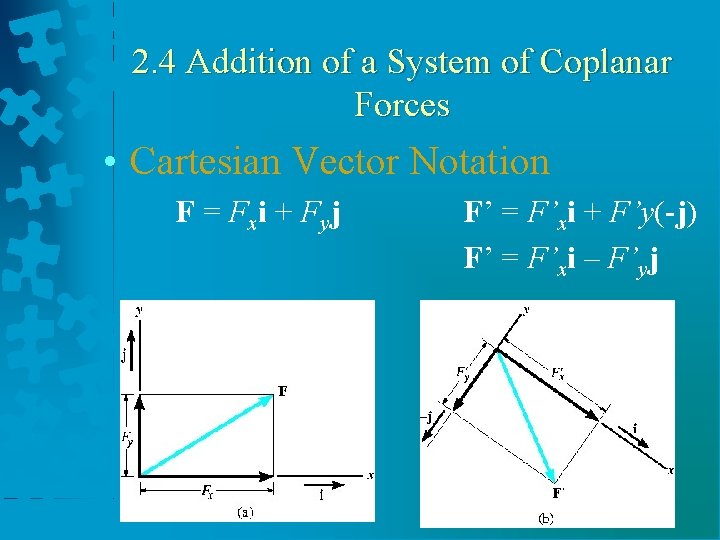
2. 4 Addition of a System of Coplanar Forces • Cartesian Vector Notation F = F xi + F yj F’ = F’xi + F’y(-j) F’ = F’xi – F’yj

2. 4 Addition of a System of Coplanar Forces • Coplanar Force Resultants Example: Consider three coplanar forces Cartesian vector notation F 1 = F 1 xi + F 1 yj F 2 = - F 2 xi + F 2 yj F 3 = F 3 xi – F 3 yj

2. 4 Addition of a System of Coplanar Forces • Coplanar Force Resultants Vector resultant is therefore FR = F 1 + F 2 + F 3 = F 1 xi + F 1 yj - F 2 xi + F 2 yj + F 3 xi – F 3 yj = (F 1 x - F 2 x + F 3 x)i + (F 1 y + F 2 y – F 3 y)j = (FRx)i + (FRy)j

2. 4 Addition of a System of Coplanar Forces • Coplanar Force Resultants If scalar notation are used FRx = (F 1 x - F 2 x + F 3 x) FRy = (F 1 y + F 2 y – F 3 y) In all cases, FRx = ∑Fx FRy = ∑Fy * Take note of sign conventions

2. 4 Addition of a System of Coplanar Forces • Coplanar Force Resultants - Positive scalars = sense of direction along the positive coordinate axes - Negative scalars = sense of direction along the negative coordinate axes - Magnitude of FR can be found by Pythagorean Theorem

2. 4 Addition of a System of Coplanar Forces • Coplanar Force Resultants - Direction angle θ (orientation of the force) can be found by trigonometry

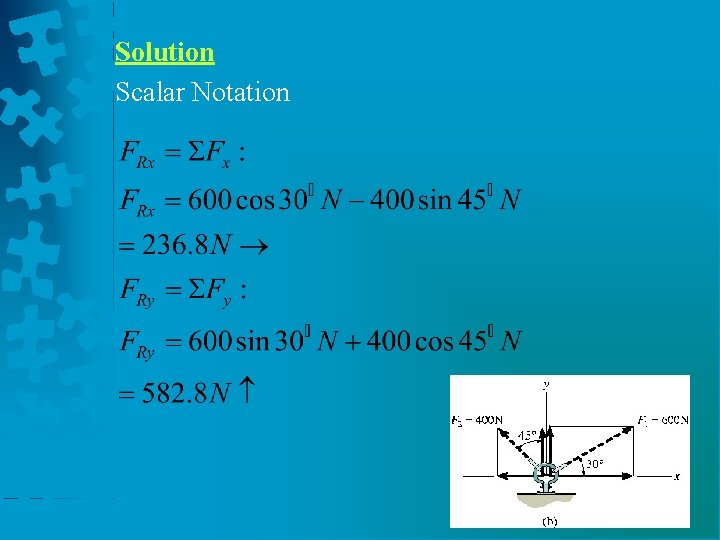
Example 3 The link is subjected to two forces F 1 and F 2. Determine the magnitude and orientation of the resultant force.

Solution Scalar Notation

Solution Resultant Force From vector addition, Direction angle θ is

Solution Cartesian Vector Notation F 1 = { 600 cos 30°i + 600 sin 30°j } N F 2 = { -400 sin 45°i + 400 cos 45°j } N Thus, FR = F 1 + F 2 = (600 cos 30°N - 400 sin 45°N)i + (600 sin 30°N + 400 cos 45°N)j = {236. 8 i + 582. 8 j}N

Problem 4: Determine the magnitude of the resultant force and its direction, measured clockwise from the positive x axis. Given: F 1 : = 70 N F 2 : = 50 N F 3 : = 65 N θ : = 30 deg φ : = 45 deg

Solution : →+ FRX : = F 1 + F 2⋅cos(θ) − F 3⋅cos(φ) +↑ FRY : = −F 2⋅ sin(θ) − F 3⋅ sin(φ) FR = FRX 2 + FRY 2 ( θ = tan-1 FRY FRX θ = 46. 5 deg ( FR = 97. 8 N

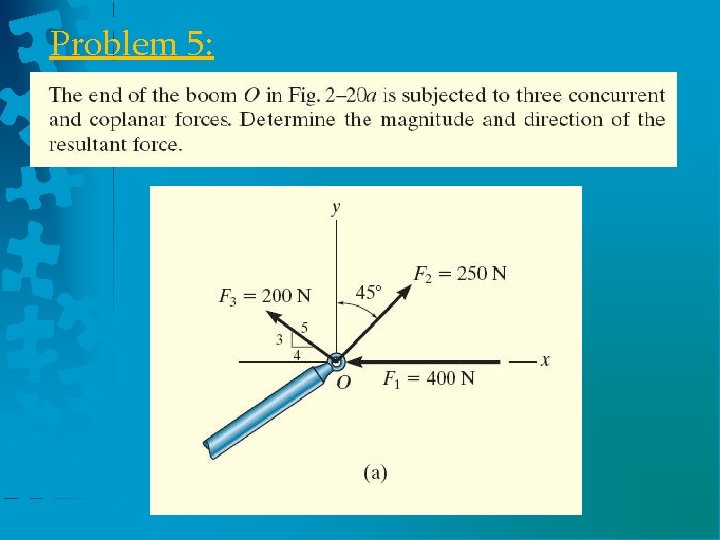
Problem 5:


2. 5 Cartesian Vectors • Right-Handed Coordinate System A rectangular or Cartesian coordinate system is said to be right-handed provided: - Thumb of right hand points in the direction of the positive z axis when the right-hand fingers are curled about this axis and directed from the positive x towards the positive y axis

2. 5 Cartesian Vectors • Rectangular Components of a Vector - A vector A may have one, two or three rectangular components along the x, y and z axes, depending on orientation - By two successive application of the parallelogram law A = A’ + Az A’ = Ax + Ay - Combing the equations, A can be expressed as A = Ax + Ay + Az

2. 5 Cartesian Vectors • Unit Vector - Direction of A can be specified using a unit vector - Unit vector has a magnitude of 1 - If A is a vector having a magnitude of A ≠ 0, unit vector having the same direction as A is expressed by u. A = A / A So that A = A u. A

2. 5 Cartesian Vectors • Unit Vector - Since A is of a certain type, like force vector, a proper set of units are used for the description - Magnitude A has the same sets of units, hence unit vector is dimensionless - A ( a positive scalar) defines magnitude of A - u. A defines the direction and sense of A

2. 5 Cartesian Vectors • Cartesian Unit Vectors - Cartesian unit vectors, i, j and k are used to designate the directions of x, y and z axes - Sense (or arrowhead) of these vectors are described by a plus or minus sign (depending on pointing towards the positive or negative axes)

2. 5 Cartesian Vectors • Cartesian Vector Representations - Three components of A act in the positive i, j and k directions A = A x i + A y j + A Zk *Note the magnitude and direction of each components are separated, easing vector algebraic operations.

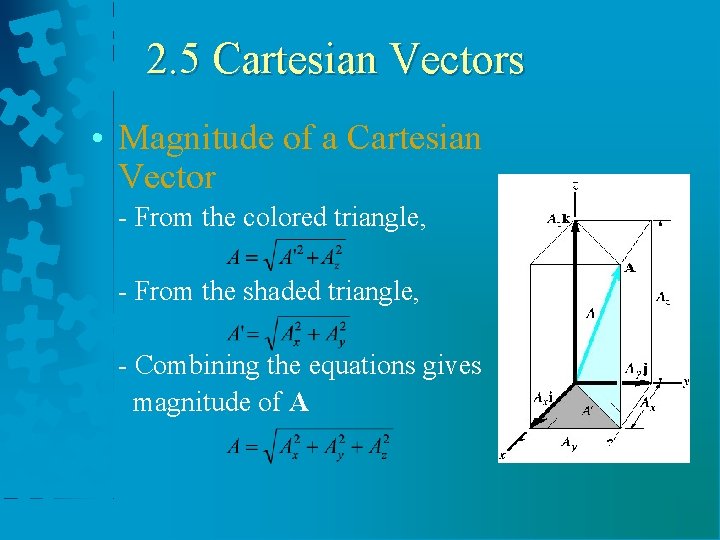
2. 5 Cartesian Vectors • Magnitude of a Cartesian Vector - From the colored triangle, - From the shaded triangle, - Combining the equations gives magnitude of A

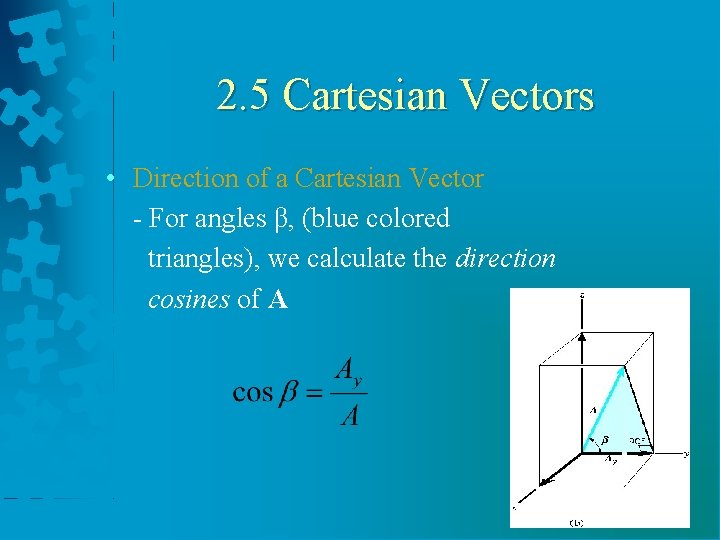
2. 5 Cartesian Vectors • Direction of a Cartesian Vector - Orientation of A is defined as the coordinate direction angles α, β and γ measured between the tail of A and the positive x, y and z axes - 0° ≤ α, β and γ ≤ 180 °

2. 5 Cartesian Vectors • Direction of a Cartesian Vector - For angles α, (blue colored triangles), we calculate the direction cosines of A

2. 5 Cartesian Vectors • Direction of a Cartesian Vector - For angles β, (blue colored triangles), we calculate the direction cosines of A

2. 5 Cartesian Vectors • Direction of a Cartesian Vector - For angles γ, (blue colored triangles), we calculate the direction cosines of A

2. 5 Cartesian Vectors • Direction of a Cartesian Vector - Angles α, β and γ can be determined by the inverse cosines - Given Then, A = A x i + A y j + A Zk u. A = A /A = (Ax/A)i + (Ay/A)j + (AZ/A)k where

2. 5 Cartesian Vectors • Direction of a Cartesian Vector - u. A can also be expressed as u. A = cosαi + cosβj + cosγk - Since and magnitude of u. A = 1, -A as expressed in Cartesian vector form A = Au. A = Acosαi + Acosβj + Acosγk = A x i + A y j + A Zk

2. 6 Addition and Subtraction of Cartesian Vectors Example Given: A = Axi + Ayj + AZk and B = Bxi + Byj + BZk Vector Addition Resultant R = A + B = (Ax + Bx)i + (Ay + By )j + (AZ + BZ) k Vector Substraction Resultant R = A - B = (Ax - Bx)i + (Ay - By )j + (AZ - BZ) k

2. 6 Addition and Subtraction of Cartesian Vectors • Concurrent Force Systems - Force resultant is the vector sum of all the forces in the system FR = ∑Fxi + ∑Fyj + ∑Fzk where ∑Fx , ∑Fy and ∑Fz represent the algebraic sums of the x, y and z or i, j or k components of each force in the system

2. 6 Addition and Subtraction of Cartesian Vectors • Force, F that the tie down rope exerts on the ground support at O is directed along the rope • Angles α, β and γ can be solved with axes x, y and z

2. 6 Addition and Subtraction of Cartesian Vectors • Cosines of their values forms a unit vector u that acts in the direction of the rope • Force F has a magnitude of F F = Fu = Fcosαi + Fcosβj + Fcosγk

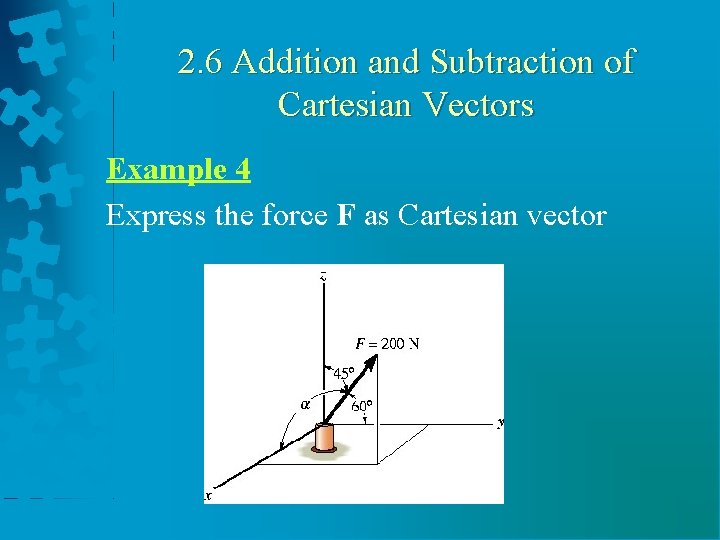
2. 6 Addition and Subtraction of Cartesian Vectors Example 4 Express the force F as Cartesian vector

2. 6 Addition and Subtraction of Cartesian Vectors Solution Since two angles are specified, the third angle is found by Two possibilities exit, namely or

2. 6 Addition and Subtraction of Cartesian Vectors Solution By inspection, α = 60° since Fx is in the +x direction Given F = 200 N F = Fcosαi + Fcosβj + Fcosγk = (200 cos 60°N)i + (200 cos 60°N)j + (200 cos 45°N)k = {100. 0 i + 100. 0 j + 141. 4 k}N Checking:

Assume lb = N


2. 7 Position Vectors • x, y, z Coordinates - Right-handed coordinate system - Positive z axis points upwards, measuring the height of an object or the altitude of a point - Points are measured relative to the origin, O.

2. 7 Position Vectors • x, y, z Coordinates Example 5: For Point A, x. A = +4 m along the x axis, y. A = +2 m along the y axis and z. A = -6 m along the z axis. Thus, A (4, 2, -6) Similarly, B (0, 2, 0) and C (6, -1, 4)

2. 7 Position Vectors • Position Vector - Position vector r is defined as a fixed vector which locates a point in space relative to another point. Eg: If r extends from the origin, O to point P (x, y, z) then, in Cartesian vector form r = xi + yj + zk

2. 7 Position Vectors • Position Vector - Position vector maybe directed from point A to point B - Designated by r or r. AB Vector addition gives r. A + r = r. B Solving r = r. B – r. A = (x. B – x. A)i + (y. B – y. A)j + (z. B –z. A)k or r = (x. B – x. A)i + (y. B – y. A)j + (z. B –z. A)k

2. 7 Position Vectors • Position Vector - The i, j, k components of the positive vector r may be formed by taking the coordinates of the tail, A (x. A, y. A, z. A) and subtract them from the head B (x. B, y. B, z. B) Note the head to tail vector addition of the three components

2. 7 Position Vectors • Length and direction of cable AB can be found by measuring A and B using the x, y, z axes • Position vector r can be established • Magnitude r represent the length of cable

2. 7 Position Vectors • Angles, α, β and γ represent the direction of the cable • Unit vector, u = r/r

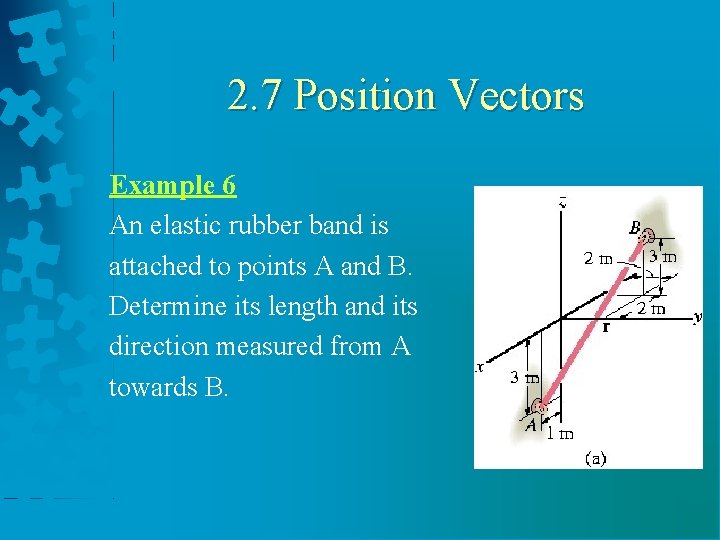
2. 7 Position Vectors Example 6 An elastic rubber band is attached to points A and B. Determine its length and its direction measured from A towards B.
![2 7 Position Vectors Solution Position vector r 2 m 1 mi 2. 7 Position Vectors Solution Position vector r = [-2 m – 1 m]i](https://slidetodoc.com/presentation_image_h/a31871047fd57c2dacb9f552ccda5c25/image-69.jpg)
2. 7 Position Vectors Solution Position vector r = [-2 m – 1 m]i + [2 m – 0]j + [3 m – (-3 m)]k = {-3 i + 2 j + 6 k}m Magnitude = length of the rubber band =7 m Unit vector in the director of r u = r /r = -3/7 i + 2/7 j + 6/7 k

2. 7 Position Vectors • Solution α = cos-1(-3/7) = 115° β = cos-1(2/7) = 73. 4° γ = cos-1(6/7) = 31. 0°

2. 8 Force Vector Directed along a Line • In 3 D problems, direction of F is specified by 2 points, through which its line of action lies • F can be formulated as a Cartesian vector F = F u = F (r/r) Note that F has units of forces (N) unlike r, with units of length (m)

2. 8 Force Vector Directed along a Line • Force F acting along the chain can be presented as a Cartesian vector by - Establish x, y, z axes - Form a position vector r along length of chain

2. 8 Force Vector Directed along a Line • Unit vector, u = r/r that defines the direction of both the chain and the force • We get F = Fu

2. 8 Force Vector Directed along a Line Example 7 The man pulls on the cord with a force of 350 N. Represent this force acting on the support A, as a Cartesian vector and determine its direction.

2. 8 Force Vector Directed along a Line Solution End points of the cord are A (0 m, 7. 5 m) and B (3 m, -2 m, 1. 5 m) r = (3 m – 0 m)i + (-2 m – 0 m)j + (1. 5 m – 7. 5 m)k = {3 i – 2 j – 6 k}m Magnitude = length of cord AB = 7 m Unit vector, u = r /r = 3/7 i - 2/7 j - 6/7 k

2. 8 Force Vector Directed along a Line Solution Force F has a magnitude of 350 N, direction specified by u F = Fu = 350 N(3/7 i - 2/7 j - 6/7 k) = {150 i - 100 j - 300 k} N α = cos-1(3/7) = 64. 6° β = cos-1(-2/7) = 107° γ = cos-1(-6/7) = 149°

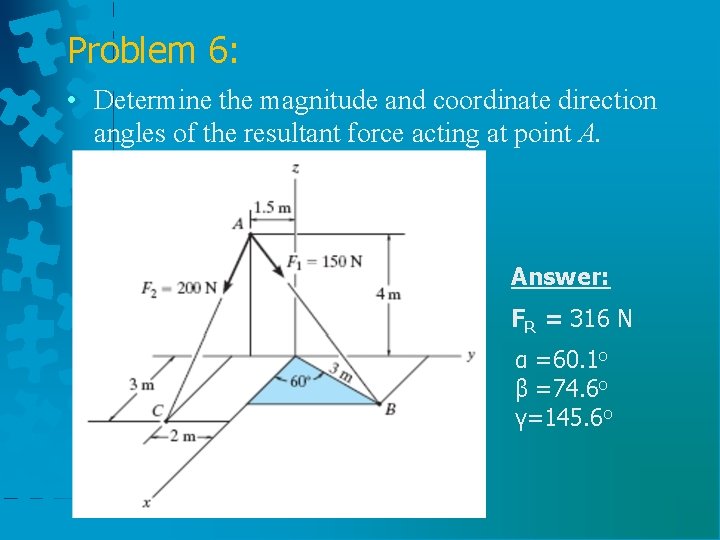
Problem 6: • Determine the magnitude and coordinate direction angles of the resultant force acting at point A. Answer: FR = 316 N α =60. 1 o β =74. 6 o γ=145. 6 o

2. 9 Dot Product • Dot product of vectors A and B is written as A·B (Read A dot B) • Define the magnitudes of A and B and the angle between their tails A·B = AB cos θ where 0°≤ θ ≤ 180°

2. 9 Dot Product Laws of Operation 1. Commutative law A·B = B·A 2. Multiplication by a scalar a(A·B) = (a. A)·B = A·(a. B) = (A·B)a 3. Distribution law A·(B + D) = (A·B) + (A·D)

2. 9 Dot Product Cartesian Vector Formulation - Dot product of Cartesian unit vectors Eg: i·i = (1)(1) cos 0° = 1 and i·j = (1)(1) cos 90° = 0 - Similarly i·i = 1 j·j = 1 k·k = 1 i·j = 0 i·k = 0 j·k = 0

2. 9 Dot Product • Cartesian Vector Formulation - Dot product of 2 vectors A and B A·B = (Axi + Ayj + Azk)· (Bxi + Byj + Bzk) = Ax. Bx(i·i) + Ax. By(i·j) + Ax. Bz(i·k) + Ay. Bx(j·i) + Ay. By(j·j) + Ay. Bz(j·k) + Az. Bx(k·i) + Az. By(k·j) + Az. Bz(k·k) = A x. B x + A y. B y + A z B z Note: since result is a scalar, be careful of including any unit vectors in the result
 Engineering mechanics chapter 2
Engineering mechanics chapter 2 Statics chapter 2
Statics chapter 2 Engineering mechanics statics in si units
Engineering mechanics statics in si units Cartesian vectors statics
Cartesian vectors statics Static equilibrium
Static equilibrium What is line of action
What is line of action Vector mechanics for engineers: statics 10th edition
Vector mechanics for engineers: statics 10th edition Vector mechanics
Vector mechanics Vector mechanics for engineers statics 10th edition
Vector mechanics for engineers statics 10th edition Vector mechanics for engineers 10th edition
Vector mechanics for engineers 10th edition Shear force statics
Shear force statics 2 force members
2 force members Force system statics
Force system statics Statics of structures
Statics of structures Friction chapter in engineering mechanics
Friction chapter in engineering mechanics A crane
A crane Force vectors
Force vectors Shaik mohammad tajuddin
Shaik mohammad tajuddin Mohammad vesal
Mohammad vesal Mohammad ali javidian
Mohammad ali javidian Dr nur mohammad hadi zahalan
Dr nur mohammad hadi zahalan Pearo-nn
Pearo-nn Dr mohammad khan
Dr mohammad khan Dr mohammad aman
Dr mohammad aman Dr mohammad aman
Dr mohammad aman Mohammad sharifkhani
Mohammad sharifkhani Mohammad sharifkhani
Mohammad sharifkhani Mohammad ghoreishi
Mohammad ghoreishi Anovulation who classification
Anovulation who classification Dr mohamed bashar shala
Dr mohamed bashar shala Mohammad sharifkhani
Mohammad sharifkhani Alaa mohammad fouad
Alaa mohammad fouad Mohammad arjomand
Mohammad arjomand Mohammad arjomand
Mohammad arjomand Mohammad ridwan bkn
Mohammad ridwan bkn Fat embolism medscape
Fat embolism medscape Mohammad sadegh rasooli
Mohammad sadegh rasooli Mohammad alipour
Mohammad alipour Mohammad keshavarz
Mohammad keshavarz Bones of pelvic girdle
Bones of pelvic girdle Dr elham altaf
Dr elham altaf Mohammad ali abtahi
Mohammad ali abtahi Mohammad irfan bowdoin
Mohammad irfan bowdoin Kongres melayu 1939 dan 1940
Kongres melayu 1939 dan 1940 Buoyancy force in fluid mechanics
Buoyancy force in fluid mechanics Statics
Statics Statics chapter 3
Statics chapter 3 Hooke의 법칙
Hooke의 법칙 Statics chapter 9
Statics chapter 9 Statics chapter 6
Statics chapter 6 Statics chapter 1
Statics chapter 1 Statics
Statics The 30 kg homogeneous cylinder of 400mm diameter
The 30 kg homogeneous cylinder of 400mm diameter Centroid applied mechanics
Centroid applied mechanics Centroid in engineering mechanics
Centroid in engineering mechanics Free body diagram in engineering mechanics
Free body diagram in engineering mechanics Frames in engineering mechanics
Frames in engineering mechanics Particle equilibrium in 2d and 3d engineering mechanics
Particle equilibrium in 2d and 3d engineering mechanics Kinetics of a rigid body
Kinetics of a rigid body Virtual work mechanics
Virtual work mechanics Centroid and centre of gravity in engineering mechanics
Centroid and centre of gravity in engineering mechanics Me 101 engineering mechanics
Me 101 engineering mechanics Centroid formula
Centroid formula Engineering mechanics
Engineering mechanics Belt friction formula
Belt friction formula Internal forces in structures engineering mechanics
Internal forces in structures engineering mechanics Mechanics static
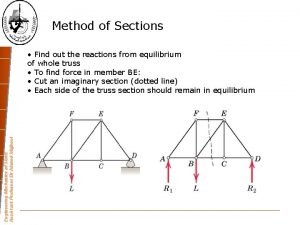
Mechanics static The truss used to support a balcony is subjected to
The truss used to support a balcony is subjected to Engineering mechanics
Engineering mechanics Hibbeler dynamics
Hibbeler dynamics Mechanics
Mechanics Moments in engineering
Moments in engineering Improperly constrained
Improperly constrained Static mechanics
Static mechanics Engineering mechanics
Engineering mechanics Dynamics
Dynamics Zero force members quiz online
Zero force members quiz online Engineering mechanics
Engineering mechanics Engineering mechanics
Engineering mechanics Chapter 3 vectors worksheets
Chapter 3 vectors worksheets Chapter 12 vectors and the geometry of space
Chapter 12 vectors and the geometry of space Chapter 12 vectors and the geometry of space solutions
Chapter 12 vectors and the geometry of space solutions