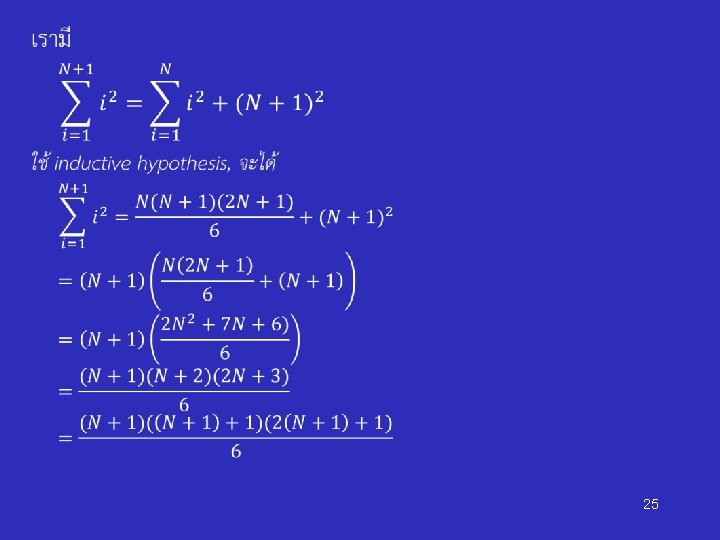1 A Recursively Defined Functions 1 Define recursively





















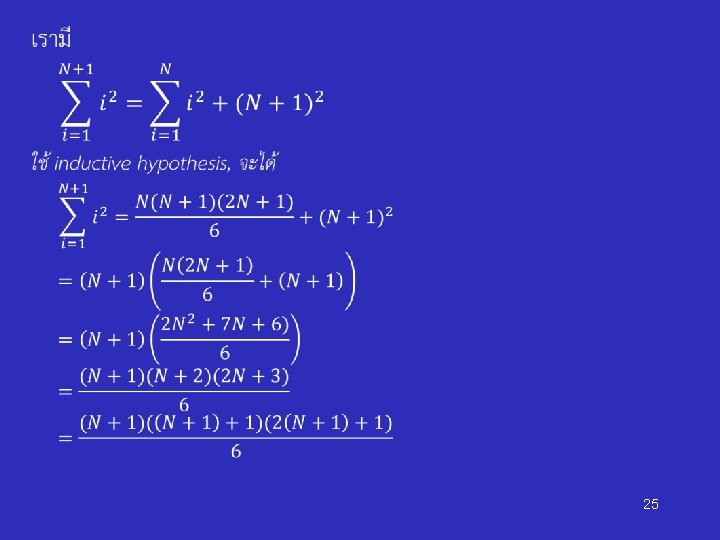




- Slides: 29

1 A Recursively Defined Functions 1

Define recursively the factorial function SOLUTION: Recall that the factorial function f is defined by f(n) = n!, where f(0) = 1. Since n! = n(n - 1)!, f can be defined recursively as follows: f(0) = 1 ← initial condition f(n) = n∙f(n - 1), n ≥ 1 recurrence relation ← 2

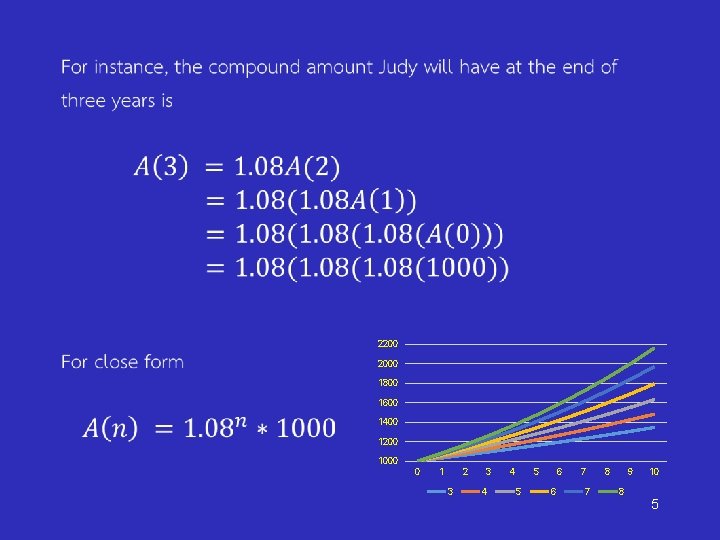
Suppose we would like to compute f(3) using this recursive definition. f(3) = 3 ∙ f(2) = 2 ∙ f(1) = 1 ∙ f(0) = 1 3


• 2200 2000 1800 1600 1400 1200 1000 0 1 2 3 3 4 4 5 5 6 6 7 7 8 9 8 10 5

The handshake problem: There are n guests at a ball. Each person shakes hands with everybody else exactly once. Define recursively the number of handshakes h(n) that occur. SOLUTION: Clearly, h(1) = 0, so let n > 2. Let X be one of the guests. By definition, the number of handshakes made by the remaining n - 1 guests among themselves is h(n - 1). Now person X shakes hands with each of these n - 1 guests, yielding n - 1 additional 6 handshakes.

Thus h(n) can be defined recursively as follows: h(1) = 0 ← initial condition h(n) = h(n - 1) + (n - 1), n > 2 ← recurrence relation 7

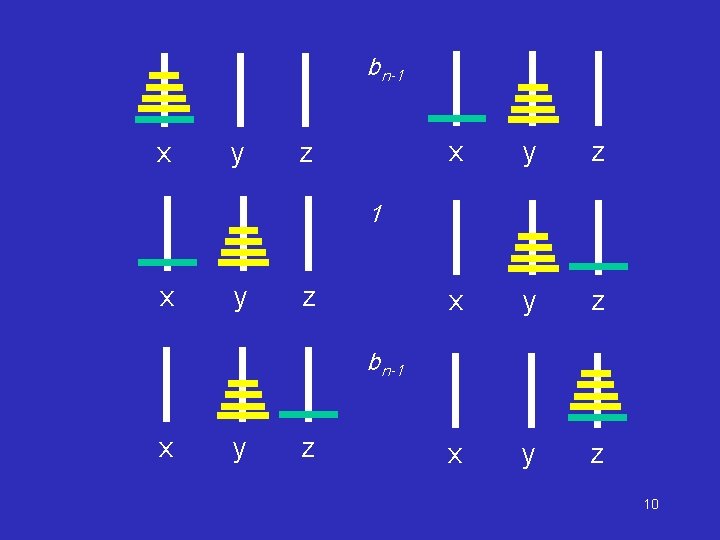
Tower of Brahma (Tower of Hanoi) According to a legend of India, at the beginning of creation, God stacked 64 golden disk on one of three diamond pegs on a brass platform in the temple of Brahma at Benares. The priest on duty were asked to move the disk for peg X to peg Z using Y as an auxiliary peg under the following condition only one disk can be moved at a time No disk can be placed on the top of a smaller disk The priests were told that the world would end when the job was completed. X Y Z 8


bn-1 x y z 1 x y z bn-1 x y z 10


Imagine n lines in a plane such that no two lines are parallel, and no three are concurrent. Let fn denote the number of distinct regions into which the plane is divided by them. Define fn recursively. SOLUTION: If there is just one line l 1 in the plane, then f 1 = 2 Now consider a second line l 2, it is intersected at exactly one point by l 1. Each half of l 2 divides an original region into two, adding two more regions. l 1 1 2 l 2 4 l 2 Thus f 2 = f 1 + 2 = 4. Suppose we add a third line l 3. It is intersected by l 1 and l 2 in two points; in other words, line l 3 is divided by l 1 and l 2 into three parts. Each portion divides an existing region into two, yielding three new regions. So f 3 = f 2 + 3 = 7. 1 3 l 1 2 l 1 1 2 4 3 7 6 5 l 3


Let an denote the number of times the assignment statement x x + 1 is executed by the following nested for loops. Defined an recursively. for i = 1 to n do for j = 1 to i do for k = 1 to j do x x + 1 First, we must find the initial condition satisfied by an. When n = 1, i=j=k=1, so the assignment statement is executed exactly once. Thus a 1 =1 Let n ≥ 2. As i runs from 1 through n-1, be definition, the statement is executed an-1 times. When i = n, the inner loops become: for j = 1 to n do for k = 1 to j do x x + 1


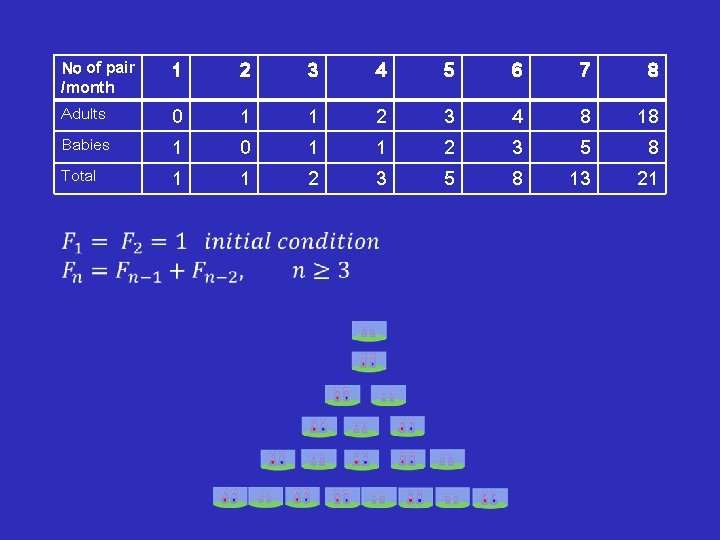
Fibonacci number Fibonacci considers the growth of an idealized (biologically unrealistic) rabbit population, assuming that: a newly born pair of rabbits, one male, one female, are put in a field; rabbits are able to mate at the age of one month so that at the end of its second month a female can produce another pair of rabbits; rabbits never die and a mating pair always produces one new pair (one male, one female) every month from the second month on. The puzzle that Fibonacci posed was: how many pairs will there be in one year? 16

• • At the end of the first month, they mate, but there is still only 1 pair. At the end of the second month the female produces a new pair, so now there are 2 pairs of rabbits in the field. At the end of the third month, the original female produces a second pair, making 3 pairs in all in the field. At the end of the fourth month, the original female has produced yet another new pair, and the female born two months ago also produces her first pair, making 5 pairs. At the end of the nth month, the number of pairs of rabbits is equal to the number of new pairs (which is the number of pairs in month n − 2) plus the number of pairs 17 alive last month

No of pair /month 1 2 3 4 5 6 7 8 Adults 0 1 1 2 3 4 8 18 Babies 1 0 1 1 2 3 5 8 Total 1 1 2 3 5 8 13 21 •

Mathematical Induction Examples 19