1 3 Matrices and Matrix Operations A matrix

Matrices The entry that occurs in row i and column j of a matrix

The entry in row I and column j of a matrix A is also

Operations on Matrices Two matrices are defined to be equal if they have the

If A is any matrix and c is any scalar (real number), then the

If are matrices of the same size and Is called a linear combination of

In general, if The entry is an m. Xr matrix and is an r.

Partitioned Matrices A matrix can be subdivided or partitioned into smaller matrices by inserting

Matrix Multiplication by Columns and by Rows jth column matrix of AB = A

Matrix Products as Linear Combinations Row and column matrices provide an alternative way of

In words, the product Ax of a matrix A with a column matrix x

It follows that the jth column matrix of a product AB is a linear

Let then the original system of linear equations can be replaced by the matrix

Transpose of a Matrix If A is any m×n matrix, then the transpose of

Trace of a Matrix If A is a square matrix, then the trace of

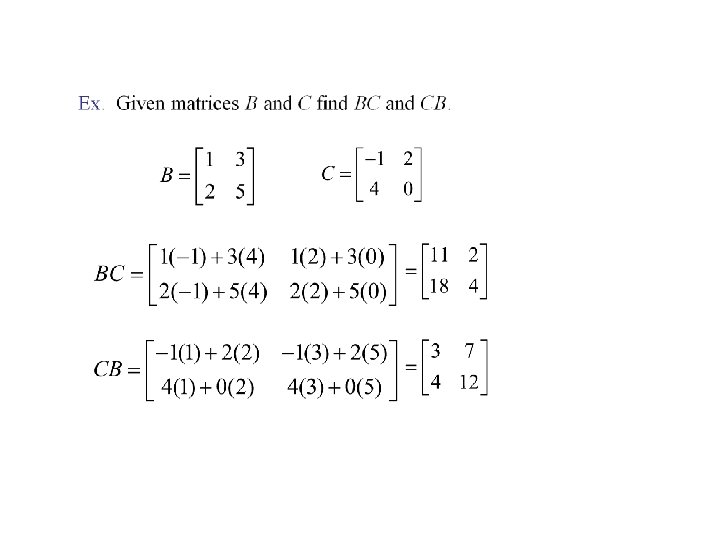
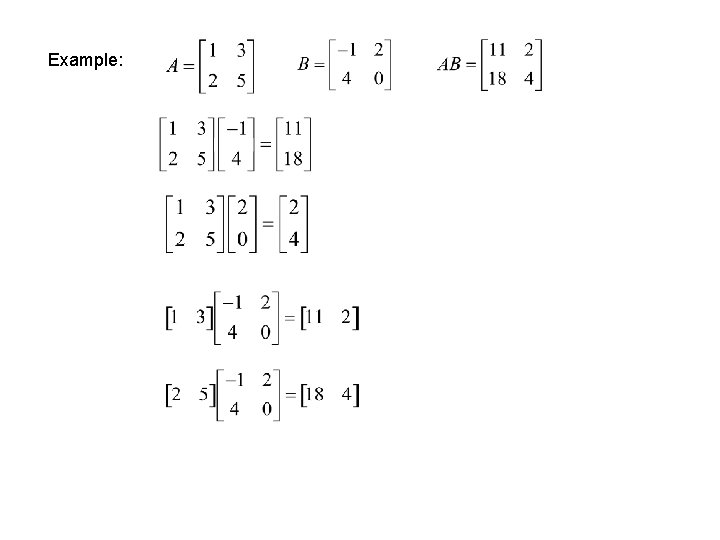
Slides: 20

Download presentation

1. 3 Matrices and Matrix Operations. A matrix is a rectangular array of numbers. The numbers in the arry are called the Entries in the matrix. The size of a matrix is described in terms of number of rows and columns in contains. A matrix with only one column is called a column matrix (or a column vector). A matrix with only one row is called a row matrix (or a row vector). Example:

Matrices The entry that occurs in row i and column j of a matrix of A will be denoted by aij. A general 3 X 4 matrix might be written as A general m. Xn matrix as It can be written as

The entry in row I and column j of a matrix A is also commonly denoted by the Symbol Example: A general 1 Xn row matrix a and a general m. X 1 column matrix b would be written as A matrix A with n rows and n columns is called a square matrix of order n, and the Shaded entries of A are said to be on the main diagonal of A

Operations on Matrices Two matrices are defined to be equal if they have the same size and their Corresponding entries are equal. In matrix notation, if A=B if and only if have the same size, then for all i and j. If A and B are matrices of the same size, then the sum A+B is the matrix obtained by Adding the entries of B to the corresponding entries of A, and the difference A-B is The matrix obtained by subtracting the entries of B from the corresponding entries of A. Matrices of different sizes cannot be added or subtracted. In matrix notation, if , then

If A is any matrix and c is any scalar (real number), then the product c. A is the matrix Obtained by multiplying each entry of the matrix A by c. The matrix c. A is caid to be A scalar multiple of A. In matrix notation, if A= , then

If are matrices of the same size and Is called a linear combination of are scalars, then with coefficients If A is an m×r matrix and B is an r×n matrix, then the product AB is the m×n matrix whose entries are determined as follows. To find the entry in row i and column j of AB, single out row i from the matrix A and column j from the matrix B. Multiply the corresponding entries from the row and column together and then add up the resulting products The definition of matrix multiplication requires that the number of columns of the First factor A be the same as the number of rows of the second factor B in order To form the product AB. If this condition is not satisfied, the product is undefined.

In general, if The entry is an m. Xr matrix and is an r. Xn matrix, then in row i and column j of AB is given by

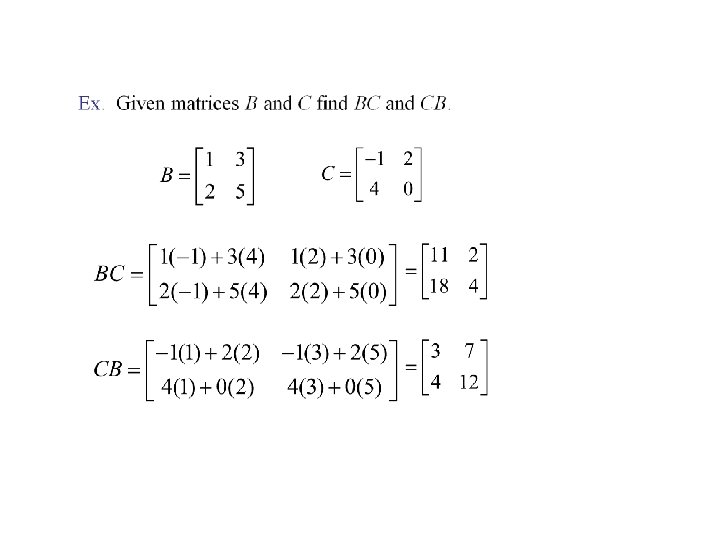
Partitioned Matrices A matrix can be subdivided or partitioned into smaller matrices by inserting horizontal and vertical rules between selected rows and columns Example

Matrix Multiplication by Columns and by Rows jth column matrix of AB = A [ jth column matrix of B ] ith row matrix of AB = [ ith row matrix of A ] B If a 1, a 2, … , am denote the row matrices of A and b 1, b 2, . . . , bn denote the column matrices of B, then it follows that

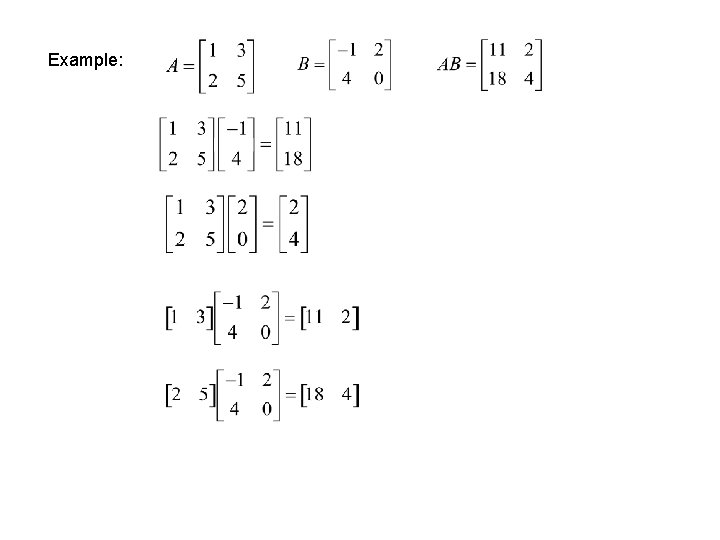
Example:

Matrix Products as Linear Combinations Row and column matrices provide an alternative way of thinking about matrix multiplication.

In words, the product Ax of a matrix A with a column matrix x is a linear combination Of the column matrices of A with the coefficients coming from the matrix x Example: Similarly, you can show that The product y. A of a 1 Xm matrix y with an m. Xn matrix A is a linear combination of the Row matrices of A with scalar coefficients coming from y. Example

It follows that the jth column matrix of a product AB is a linear combination of the Column matrices of A with the coefficients coming from the jth column of B. Example:

Matrix Form of a Linear System

Let then the original system of linear equations can be replaced by the matrix equation Ax=b Here A is called the coefficient matrix.

Transpose of a Matrix If A is any m×n matrix, then the transpose of A, denoted by , is defined to be the n×m matrix that results from interchanging the rows and columns of A; That is, the first column of is the first row of A, the second column of is the second row of A, and so forth. Example:

Trace of a Matrix If A is a square matrix, then the trace of A , denoted by tr(A), is defined to be the sum of the entries on the main diagonal of A. The trace of A is undefined if A is not a square matrix. Example: