ZKLADY INFORMATIKY Rovnomrn a nerovnomrn kdy 1 Vznik

ZÁKLADY INFORMATIKY – Rovnoměrné a nerovnoměrné kódy 1. Vznik a vývoj teorie informace 2. Matematický aparát v teorii informace • • 3. Základy teorie pravděpodobnosti – Náhodné veličiny Číselné soustavy Informace • • Základní pojmy – jednotka a zobrazení informace, informační hodnota Entropie – vlastnosti entropie Zdroje zpráv – spojité zdroje zpráv, diskrétní zdroje zpráv Přenos informace – vlastnosti přenosu kanálů, poruchy a šumy přenosu, způsoby boje proti šumu 4. Kódování • • 5. Elementární teorie kódování Rovnoměrné kódy – telegrafní kód Nerovnoměrné kódy – Morseova abeceda, konstrukce nerovnoměrných kódů Efektivní kódy – Shannonova – Fanova metoda, Huffmanova metoda Bezpečností kódy • • • Zabezpečující schopnosti kódů, Systematické kódy, Nesystematické kódy

y d ó k é n r ě m o n v o R

Rovnoměrné kódy jsou takové kódy, u kterých se každému znaku zdrojové abecedy přiřadí stejný počet kódových znaků. Z toho důvodu mají tyto kódy velkou výhodu při dekódování. Nerozšířenější příklady rovnoměrných kódů jsou: telegrafní kód a ASCII kód.

Telegrafní kód se používá v dálnopisných sítích. Verze MTA 2 se používá už od roku 1932. Roku 1820 Oersted zjistil, že kolem elektrického vodiče (drátu) vzniká elektromagnetické pole schopné otáčet ručičkou kompasu.

Na tomto principu vznikl elektromagnet a další vývoj už byl "jen" otázkou dobrých nápadů. V roce 1832 se objevují první jehlové telegrafy (tehdy se říkalo galvanoměry). galvanoměry Systém používá pěti jehlových ukazatelů k indikaci zvláštního kódu, jehož význam se pak hledá ve slovníku. V tom samém roce se objevuje Samuel F. B. Morse jehož jméno je spojeno s ELEKTROMAGNETICKÝM telegrafem.

O rok později už předvádí své první zařízení pro přenos signálů po drátě: na jednom konci zapíná vypínač a na druhém označuje papírovou pásku. V roce 1840 dostává MORSE patent na záznamový elektrický telegraf a telegrafní symboly. Zdrojová abeceda obsahuje • všechny písmena anglické abecedy, číslice 0, 1, . . . , 9 • a některá interpunkční znaménka. Každému znaku zdrojové abecedy je přiřazena konkrétní pětice kódových znaků 0 a 1.

Protože písmen anglické abecedy je 26, k tomu ještě 10 číslic (a nějaká interpunkční znaménka), kapacita kódu, která je rovna 25=32 znaků, je nepostačující. Tento problém se řeší tak, že se většina pětic znaků využívá dvakrát. K jejich rozlišení se používá tzv. změna registru. Pro písmenovou změnu je přiřazené kódové slovo 11111 a pro číslicovou změnu 11011. To umožňuje, abychom mohli zakódovat 2. 25 -2=62 zdrojových znaků.

Příklad: Pomocí tabulky telegrafního kódu zakódujte zprávu „MS DOS 7. 0“ 11111 00111 10100 M S 00100 11011 Písmenová změna 10100 S mezera číslicová změna 00100 10010 00011 mezera D 11100 00111 01101 . 0 7 O

Příklad: Abeceda zdroje má tři znaky A={a 1, a 2, a 3}. Zakódujte znaky zdroje rovnoměrným kódem. Protože existují 22 = 4 různé dvojice kódových znaků 0 a 1 stačí kódovat takto: a 1 = 00 a 2 = 01 a 3 = 10

ASCII kód V současné době, době počítačů a počítačových sítí ztrácí dálnopisy význam. Telegrafní kód je již dlouho nepostačující současným potřebám přenosu dat. V šedesátých letech proto vznikl v USA kód vyvinutý speciálně pro mikropočítače - ASCII Zdrojová abeceda obsahuje kromě písmen anglické abecedy a číslic i znaky používané ve výpočetní technice (malá písmena, algebraické znaky +, , , =. . . ). Každému z 27=128 znaků zdrojové abecedy se přiřadí sedmice kódových znaků 0 a 1.

Zdokonalováním ASCII kódu se vyvinulo mnoho dalších rovnoměrných kódů např. ISO-7, ISO-8 Z ISO-7 se vycházelo při sestavování osmi prvkového kódu ISO-8. Osmý paritní bit ISO-7 byl nahrazen významovým bitem umožňujícím vyjádřit malá i velká písmena např. azbuky a v české verzi písmena s háčky a čárkami (prvních 7 sloupců kódové tabulky ISO-8 je shodných se sloupci ISO-7).

Příklad: Pomocí tabulky ISO-7 kódu zakódujte zprávu „Technologická Fakulta“

y d ó k é n r ě m o n v o r Ne

Nerovnoměrné kódy jsou takové kódy, kdy se jednotlivým znakům zdrojové abecedy přiřazují kódová slova, která mají různý počet znaků Nejznámějším a nejrozšířenějším příkladem tohoto kódování je Morseova abeceda.

Morseova abeceda Charakteristickou vlastností tohoto kódu je, že zohledňuje pravděpodobnostní strukturu zdrojové abecedy. To znamená, že znakům s vyšší frekvencí výskytu je přiřazeno kratší kódové slovo a naopak znakům s nižší frekvencí výskytu delší kódové slovo.

Je obecně známo, že Morseova abeceda obsahuje znaky. (tečka) a - (čárka). Bližším zkoumáním bychom zjistili, že to není úplně pravda protože kódová abeceda obsahuje znaky tři. Plyne to z pravidel vysílání: - čas vysílání znaku. je t - čas vysílání znaku - je 3 t - mezi znaky. a - je pauza t - mezi zdrojovými znaky je pauza 3 t - mezi zdrojovými slovy je pauza 6 t

Z toho kódová abeceda je: Y={ y 1, y 2, y 3 } y 1=. + t y 2= - + t y 3= 3 t

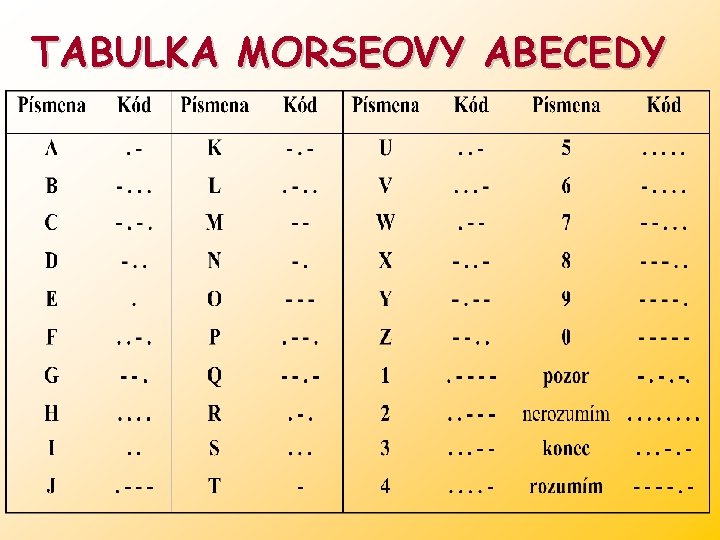
TABULKA MORSEOVY ABECEDY

Příklad: Pomocí tabulky Morseové abecedy zakódujte zprávu „ZIMNÍ SEMESTR“ ZDE JE MOŽNO SI VYZKOUŠET MORSEOVU ABECEDU a) do Morseové abecedy b) do kódové abecedy Y Řešení: Z I M N Í S E M E S T R a) --. . -- -. . . . -- . . -. -. b) y 2 y 1 y 1 y 3 y 2 y 1 y 3 y 1 y 1 y 3 y 2 y 3 y 1 y 2 y 1 y 3

Konstrukce nerovnoměrných kódů Ke konstrukci nerovnoměrných kódů se využívají grafy. V teorii grafů se takovýto graf nazývá strom. Strom obsahuje uzly a z každého uzlu stromu vycházejí dvě hrany. Posloupnost za sebou následujících hran se nazývá cesta.

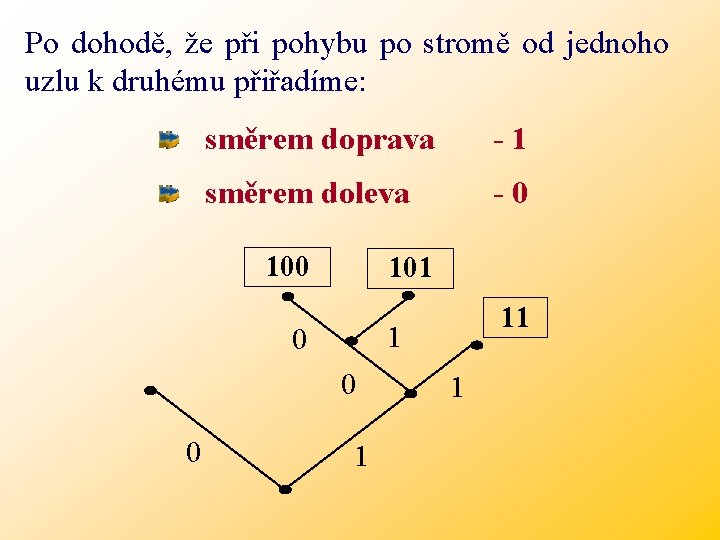
Po dohodě, že při pohybu po stromě od jednoho uzlu k druhému přiřadíme: směrem doprava -1 směrem doleva -0 101 1 0 0 0 11 1 1

Z toho vyplývá, že každé cestě začínající v kořeni stromu odpovídá nějaké kódové slovo a každému kódovému slovu je jednoznačně přiřazena nějaká cesta začínající v kořeni stromu. Platí: Přiřadíme-li zdrojovému znaku ai nějakou cestu začínající v kořeni stromu, pak žádné jiné zdrojové slovo aj ai nemůže mít přiřazenou cestu, která by obsahovala celou cestu přiřazenou znaku ai.

Toto pravidlo se označuje jako vlastnost předpony - P (prefix property) a takovéto kódy se nazývají P-kódy. Tyto kódy jsou jednoznačně dekódovatelné! Jejich dekódování spočívá v postupném ověřování patří-li přijaté kódové slovo (nebo jeho část) do kódu, nebo ne.

Uvažujme, že pro zdrojovou abecedu A={a 1, a 2, . . . , a. N} zadáme dopředu délku kódových slov příslušících jednotlivým zdrojovým znakům. Budeme tedy vyžadovat, aby znaku ai A odpovídalo kódové slovo délky ni, i=1, . . . , N. N Mc Millan (1956) dokázal, že pro jednoznačně dekódovatelný kód s délkami kódových slov n 1, n 2, . . . , n. N platí: Zde je možné vyzkoušet Mc Millanovu podmínku:

Příklad: Sestrojte kód pro zdrojovou abecedu, která obsahuje 7 písmen, jsou-li dány délky jednotlivých kódových slov takto: 2, 2, 3, 3, 4, 5, 5. 5 ) Zjistíme, existuje-li takový kód pomocí Mc Millanova vztahu: 2 -2 + 2 -3 + 2 -4 + 2 -5 + 25 = = 0. 25 + 0. 125 + 0. 0625 + 0. 875 1 0. 03125 + 0. 03125 =

Znamená to, že takový kód existuje a stačí obsadit libovolné: 2 uzly na druhé úrovni 2 uzly na třetí úrovni 1 uzel na čtvrté úrovni 2 uzly na páté úrovni

) Sestrojíme jeden z možných kódů: 11010 5. úroveň 1111 4. úroveň 3. úroveň 2. úroveň 11011 100 00 101 01 1. úroveň 0 1 Výsledný kód je { 00, 01, 100, 101, 1111, 11010, 11011 }.

Začneme-li teď uvažovat o otázce kódových slov z hlediska pravděpodobnostní struktury zdrojové abecedy, přiřadíme zdrojové abecedě A={a 1, a 2, . . . , a 7 } pravděpodobnosti:

Vypočítejme teď, kolik kódových znaků musíme vyslat, chceme-li poslat zprávu obsahující 1000 zdrojových znaků: = 3400 kódových znaků Z toho vyplývá, že na jeden zdrojový znak připadne 1/1000 tzn. 3. 4 kódového znaku. ( Toto číslo je průměrná délka kódového slova při nezávislém vysílání zdrojových znaků ).