Zadania z indywidualnoci Zadanie 1 Znajd najmniejsz warto



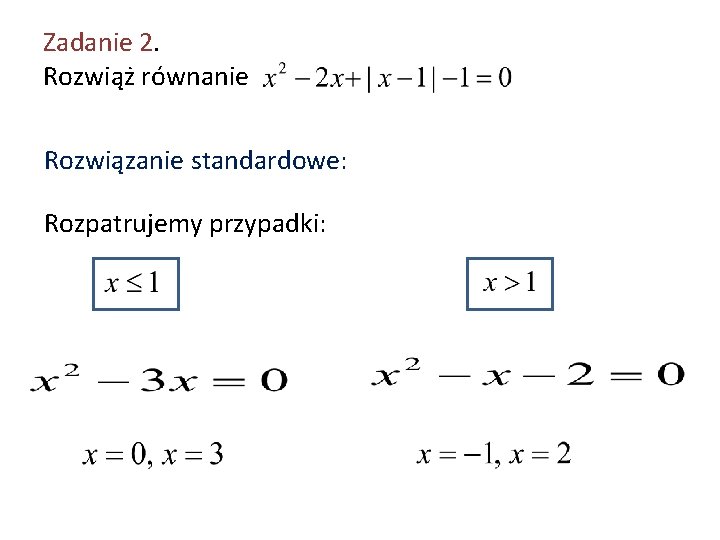
















- Slides: 21

Zadania z indywidualnością

Zadanie 1. Znajdź najmniejszą wartość wyrażenia Rozwiązanie standardowe: Wzór na najmniejszą wartość funkcji kwadratowej: Najmniejsza wartość = Δ/4 a Δ = 44, a = 1, zatem najmniejsza wartość = – 11

Zadanie 1. Znajdź najmniejszą wartość wyrażenia Rozwiązanie niestandardowe:
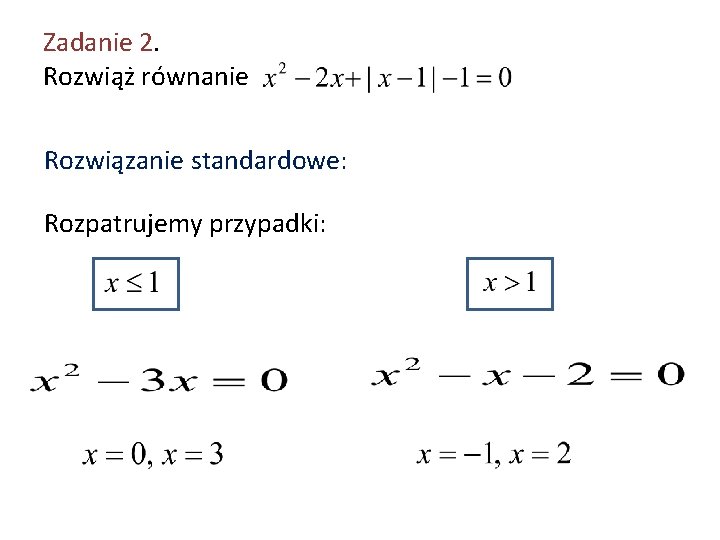
Zadanie 2. Rozwiąż równanie Rozwiązanie standardowe: Rozpatrujemy przypadki:

Zadanie 2. Rozwiąż równanie Rozwiązanie niestandardowe:

Zadanie 3. Dane są liczby rzeczywiste x, y takie, że Oblicz Rozwiązanie standardowe: Przekształcamy do postaci i dalej skąd

Zadanie 3. Dane są liczby rzeczywiste x, y takie, że Oblicz Rozwiązanie niestandardowe:

Zadanie 4. Rozwiąż równanie Rozwiązanie standardowe: Podnosimy obie strony do kwadratu, otrzymujemy równanie kwadratowe Obliczamy pierwiastki.

Zadanie 4. Rozwiąż równanie Rozwiązanie niestandardowe: Podstawiamy rozwiązujemy równanie a następnie równania

Zadanie 5. Wykaż, że jeśli wielomian ma trzy różne pierwiastki rzeczywiste, to a < 0. Rozwiązanie standardowe (? ? ? ): Z założenia istnieją k, m, n takie, że wielomian można zapisać w postaci Stąd W rezultacie z czego wynika a < 0.

Zadanie 5. Wykaż, że jeśli wielomian ma trzy różne pierwiastki rzeczywiste, to a < 0. Rozwiązanie niestandardowe (? ): Jeśli to wielomian jest funkcją rosnącą, a więc ma co najwyżej jeden pierwiastek.

Zadanie 6. Niech f będzie wielomianem o współczynnikach całkowitych. Wykaż, że jeśli c i d są różnymi liczbami całkowitymi, to c – d dzieli f(c) – f(d). Rozwiązanie standardowe: Niech Wówczas

Zadanie 6. Niech f będzie wielomianem o współczynnikach całkowitych. Wykaż, że jeśli c i d są różnymi liczbami całkowitymi, to c – d dzieli f(c) – f(d). Rozwiązanie niestandardowe: Z twierdzenia o reszcie: zatem

Zadanie 7. Zbadaj, czy istnieje wielomian w stopnia 3 o współczynnikach całkowitych, taki że w(0) = 1, w(1) =2, w(2)=3 oraz w(3)=0. Rozwiązanie standardowe: Niech Podstawiamy Układ nie ma rozwiązań w liczbach całkowitych.

Zadanie 7. Zbadaj, czy istnieje wielomian w stopnia 3 o współczynnikach całkowitych, taki że w(0) = 1, w(1) =2, w(2)=3 oraz w(3)=0. Rozwiązanie niestandardowe 1: Niech Z pierwszego warunku: d = 1. Z czwartego warunku:

Zadanie 7. Zbadaj, czy istnieje wielomian w stopnia 3 o współczynnikach całkowitych, taki że w(0) = 1, w(1) =2, w(2)=3 oraz w(3)=0. Rozwiązanie niestandardowe 2: Z pierwszego warunku: wyraz wolny = 1. Pierwiastek 3 musi dzielić wyraz wolny, czyli 1. Nie dzieli.

Zadanie 8. Niech Znajdź wszystkie wartości x, dla których w(w(x))=w(x). Rozwiązanie standardowe: Podstawiamy: a stąd

Zadanie 8. Niech Znajdź wszystkie wartości x, dla których w(w(x))=w(x). Rozwiązanie niestandardowe 1: Podstawiamy: a stąd czyli

Zadanie 8. Niech Znajdź wszystkie wartości x, dla których w(w(x))=w(x). Rozwiązanie niestandardowe 2: Jeśli w(a)=w(b), to a, b leżą symetrycznie względem osi symetrii wykresu w, czyli istnieje c takie, że x = ½ – c oraz w(x) = ½ + c. Stąd

DODATEK Zadanie bez numeru. Wykaż, że dla każdej liczby naturalnej n > 2 liczba jest niewymierna. Rozwiązanie niestandardowe: Przypuśćmy, że Wtedy wbrew Wielkiemu Twierdzeniu Fermata. czyli

Zakończenie niestandardowe: • To już jest koniec, nie ma już nic, jesteśmy wolni, możemy iść!
 Czy warto uczyć się programowania
Czy warto uczyć się programowania Dlaczego warto przeczytać chłopców z placu broni
Dlaczego warto przeczytać chłopców z placu broni Dlaczego warto być aktywnym fizycznie
Dlaczego warto być aktywnym fizycznie Slidetodoc.com
Slidetodoc.com Dlaczego warto segregować śmieci prezentacja
Dlaczego warto segregować śmieci prezentacja Czy warto przeczytać akademię pana kleksa
Czy warto przeczytać akademię pana kleksa Inkubator przedsiębiorczości oświęcim
Inkubator przedsiębiorczości oświęcim Dlaczego warto uczyć się matematyki
Dlaczego warto uczyć się matematyki Zadanie
Zadanie Schematy sieci komputerowych
Schematy sieci komputerowych Zadanie egzaminacyjne
Zadanie egzaminacyjne Wzór podania o urlop po niemiecku
Wzór podania o urlop po niemiecku Zadanie
Zadanie Zdejmując ubranie gazoszczelne ratownik
Zdejmując ubranie gazoszczelne ratownik Pierwsza koparka wykonala polowe wykopu w ciagu 6 h
Pierwsza koparka wykonala polowe wykopu w ciagu 6 h Dorsmu
Dorsmu Zadanie
Zadanie Fala materii
Fala materii Zadania addytywne przykłady
Zadania addytywne przykłady Most kolejowy
Most kolejowy Mapa pojeciowa
Mapa pojeciowa Koła niewykonalne zadanie geometryczne
Koła niewykonalne zadanie geometryczne







































