WVU Calculus Dr Vicki Sealey sealeymath wvu edu

WVU Calculus Dr. Vicki Sealey sealey@math. wvu. edu Dr. Jessica Deshler deshler@math. wvu. edu

Overview Structure of calculus courses at WVU Roles of graduate teaching assistants (GTAs) and undergraduate tutors Curriculum and methods of one of these courses (Non-Engineering Math 155) Info about nationwide AP calculus students

Introductions Tell us about yourself (name, where you teach, etc. ) Tell us about calculus at your school

Options for Calculus I Math 155 – One semester calculus I course ◦ Engineering sections Gary Ganser ◦ Non-engineering sections Vicki Sealey Math 153/154 – Two semester calculus I course Eddie Fuller/Stacey Bowling Math 150 – Business calculus Marjorie Darrah

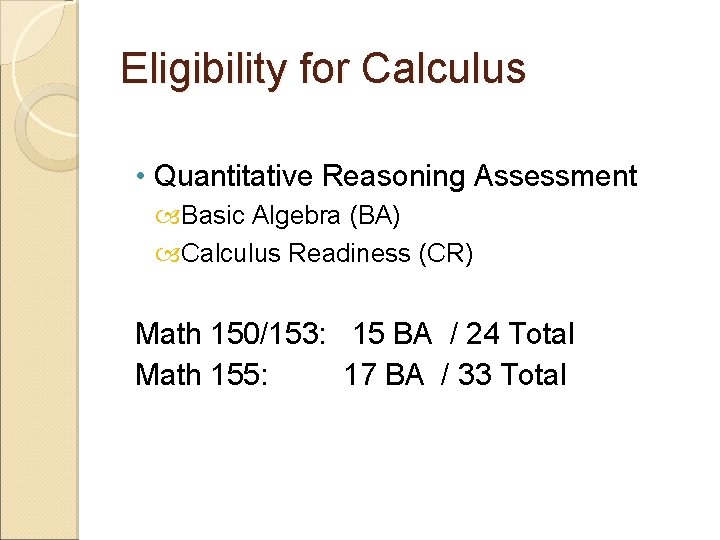
Eligibility for Calculus • Quantitative Reasoning Assessment Basic Algebra (BA) Calculus Readiness (CR) Math 150/153: 15 BA / 24 Total Math 155: 17 BA / 33 Total

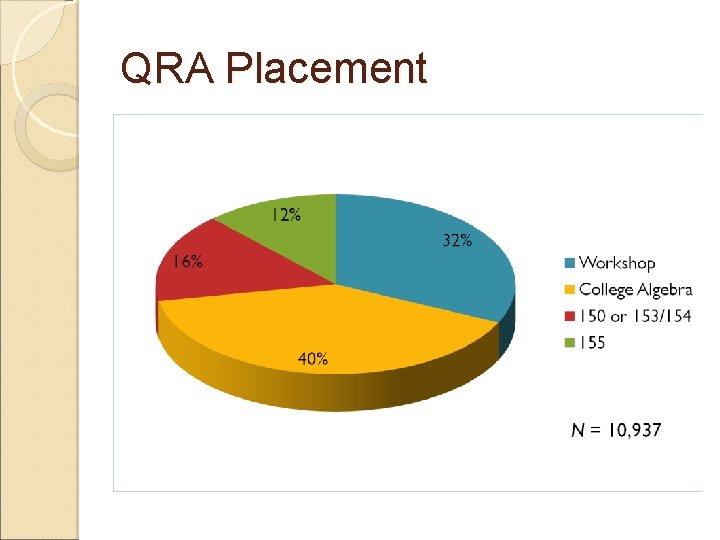
QRA Placement

Eligibility for Calculus • Course Credit Math 150: C or better in College Algebra Math 153/155: C or better in College Algebra and Trigonometry Course credit is honored over QRA scores

Eligibility for Calculus AP Credit ◦ 3 on the AB exam: placement into Math 155 ◦ 4 or 5 on AB exam: credit for Math 155 ◦ 3 on BC exam: credit for Math 155 ◦ 4 or 5 on BC exam: credit for Math 155 and Math 156

Course Structure for Math 155 Non-Engineering Textbook: Essential Calculus by James Stewart Scientific calculator required Graphing calculator strongly recommended ◦ CAS not allowed (TI-89 and above, for example) ◦ Memory cleared before each test ◦ Sometimes not allowed on quizzes

Course Structure, cont. Four credit course, but meets for an additional 50 minutes per week ◦ More time to do math (not just see math) ◦ Time for group work activities Evening exams ◦ Common across sections ◦ Common grading

Homework Roughly half online and half written Online HW common across sections ◦ We. BWor. K or Web. Assign ◦ Immediate feedback, multiple attempts ◦ Video tutorials (WA only) ◦ Each student has slightly different numbers in each question ◦ GTA answers questions through e-mail

Instructors Use an instructional team ◦ Course coordinator (Vicki) ◦ Grad student coordinator (Jessica) ◦ Lead instructor (Iwona Wojciechowska) Consistency across semesters (and within each semester) Dedication to this course

Graduate Teaching Assistants Their roles in the course: ◦ Each section has an instructor and a graduate teaching assistant (GTA) ◦ Each GTA is assigned to two sections ◦ Proctor and grade exams, quizzes ◦ Assist the instructor as needed in-class Group activities Teach up to one class per week

Graduate Assistants Professional development as novice instructors of college math ◦ Teaching experience ◦ Write exam questions ◦ Office hours – working one-on-one with students (Math Learning Center) ◦ Grading – common grading on exams, quizzes Rubrics developed by Vicki Sealey, Jessica Deshler, and by GTAs.

Other Help Math Learning Center Tutoring center in Towers dorms Shared office hours Review sessions outside of class

Curriculum Concept first approach ◦ Procedures follow the concepts ◦ Applications often motivate a need for concepts Emphasis on limits ◦ Limits of functions Holes, jumps, asymptotes ◦ Derivatives Limit of difference quotient ◦ Integrals Limit of Riemann sums

Teaching Philosophy Constructivist perspective Reflective abstraction (Piaget) ◦ Not just seeing math topics ◦ Doing something with math and reflecting on the structure Cooperative learning

AP Calculus Statistics From 1992, of students who took some form of calculus in high school ◦ 31% took precalculus in college ◦ 32% took no calculus Students who pass the AP exam do quite well in college. ◦ We’re concerned about the students who don’t pass the test but are still top students. Many of these students aren’t taking additional math courses.

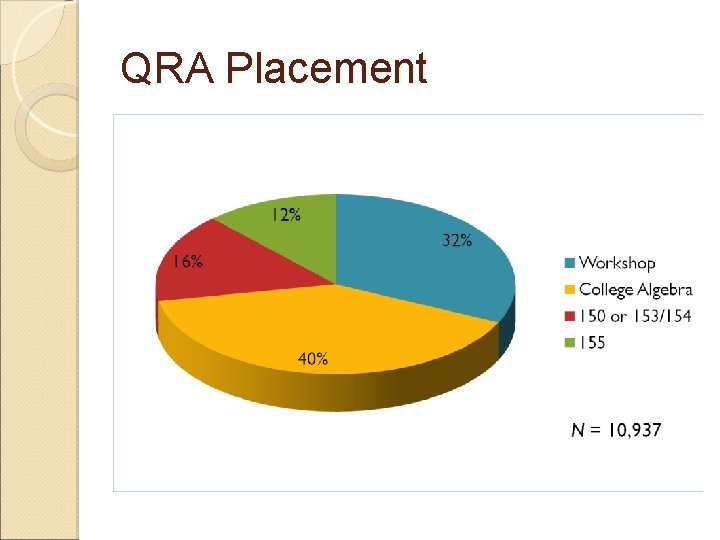
QRA Placement

ASU Calculus Statistics In a 5 -year period at ASU, of all students who received an A in precalculus and their major required at least Calculus I… 43% did not take calculus.

ASU Calculus Statistics During the same 5 -year period at ASU ◦ 43% of engineering majors ◦ 54% of math majors ◦ 51% of physical science majors ◦ 50% of technology majors who enrolled in calculus I and whose major required calculus II never earned credit in calculus II.

Our hopes College math should be a natural progression from students’ high school math courses More students interested in studying mathematics ◦ Math majors (including dual majors) ◦ Math minors ◦ Math ‘enthusiasts’