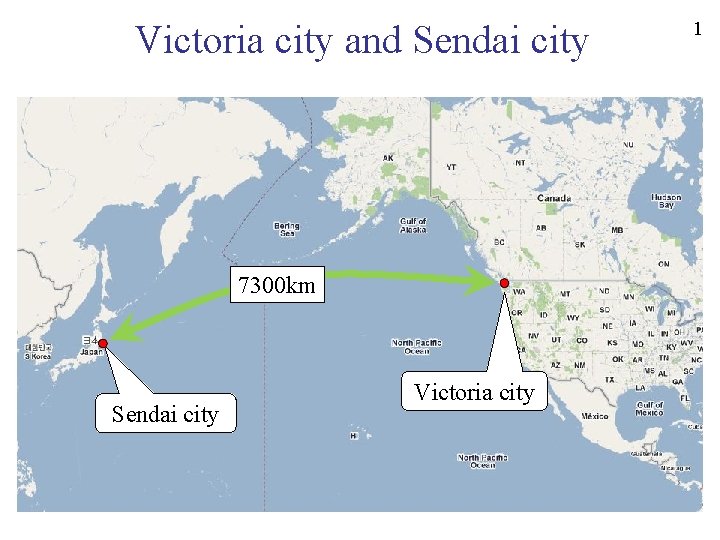
Victoria city and Sendai city 7300 km Sendai









- Slides: 50

Victoria city and Sendai city 7300 km Sendai city Victoria city 1

2 Tohoku University was established in 1907. Spring Summer Autumu Winter

GSIS, Tohoku University 3 Graduate School of Information Sciences (GSIS), Tohoku University, was established in 1993. 150 Faculties 450 students Math. Computer Science Robotics Transportation Economics Human Social Sciences Interdisciplinary School

Book 4

5 Small Grid Drawings of Planar Graphs with Balanced Bipartition Xiao Zhou Takashi Hikino Takao Nishizeki Graduate School of Information Sciences, Tohoku University, Japan

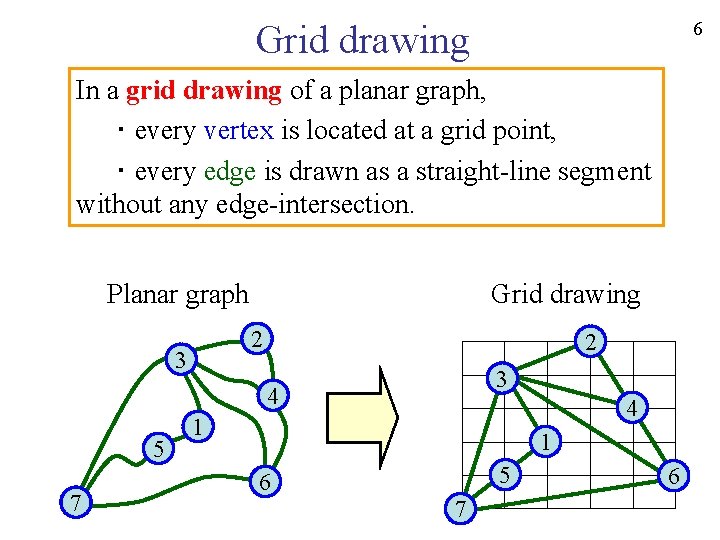
6 Grid drawing In a grid drawing of a planar graph, ・ every vertex is located at a grid point, ・ every edge is drawn as a straight-line segment without any edge-intersection. Planar graph Grid drawing 2 3 4 5 7 4 1 1 5 6 7 6

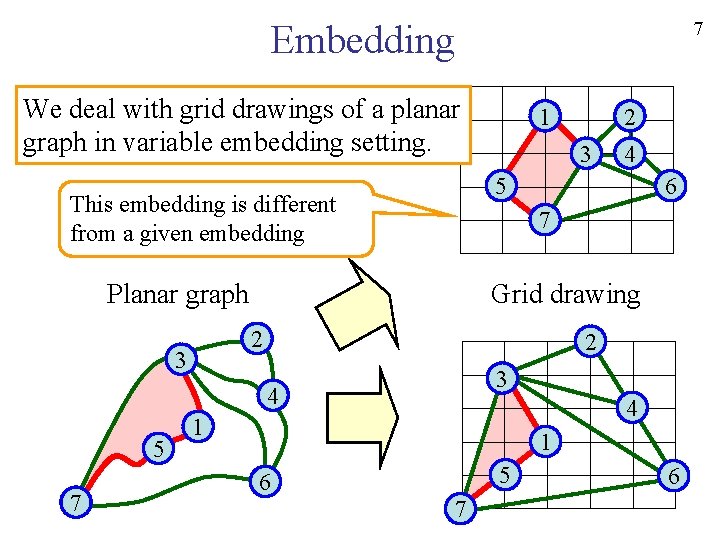
7 Embedding We deal with grid drawings of a planar graph in variable embedding setting. 4 6 Grid drawing 2 2 3 4 7 3 7 Planar graph 3 2 5 This embedding is different from a given embedding 5 1 4 1 1 5 6 7 6

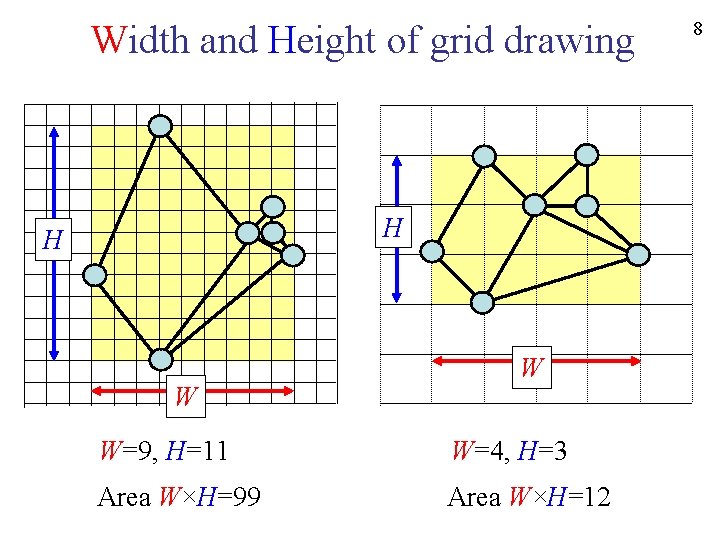
Width and Height of grid drawing H H W W W=9, H=11 W=4, H=3 Area W×H=99 Area W×H=12 8

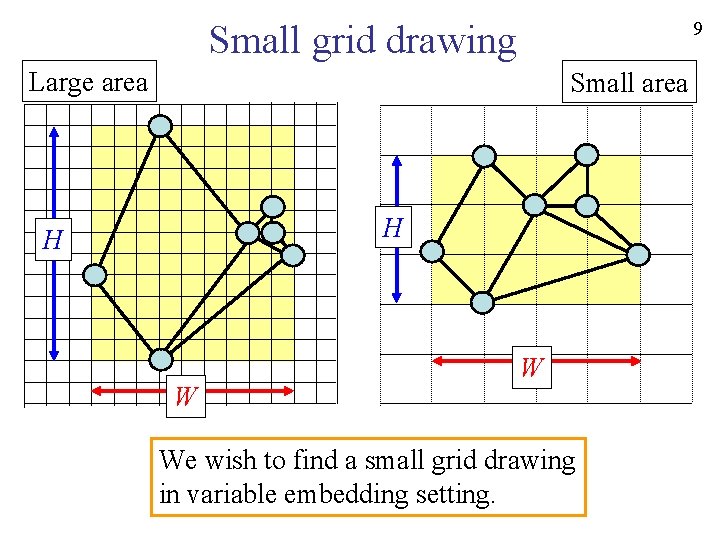
9 Small grid drawing Large area Small area H H W W We wish to find a small grid drawing in variable embedding setting.

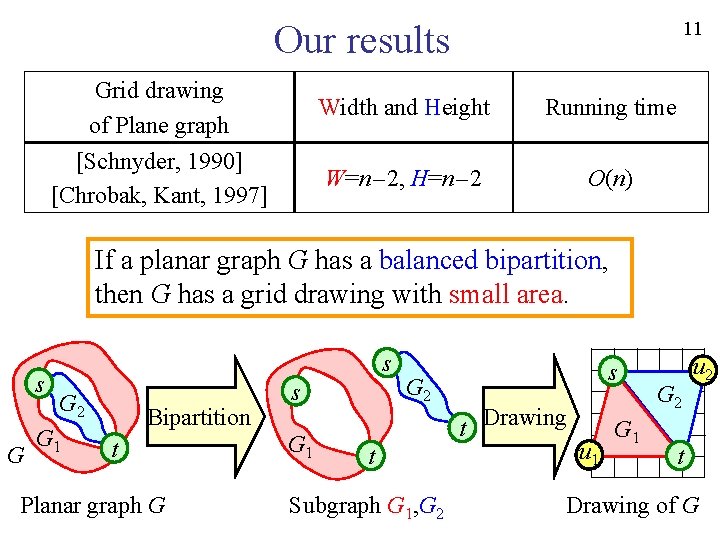
10 Known results Grid drawing of Plane graph Width and Height Running time [Schnyder, 1990] [Chrobak, Kant, 1997] W=n-2, H=n-2 O(n) n : number of vertices

11 Our results Grid drawing of Plane graph Width and Height Running time [Schnyder, 1990] [Chrobak, Kant, 1997] W=n-2, H=n-2 O(n) If a planar graph G has a balanced bipartition, then G has a grid drawing with small area. s G 2 G 1 Bipartition t Planar graph G s G 1 G 2 t Subgraph G 1, G 2 s t Drawing u 1 G 2 u 2 t Drawing of G

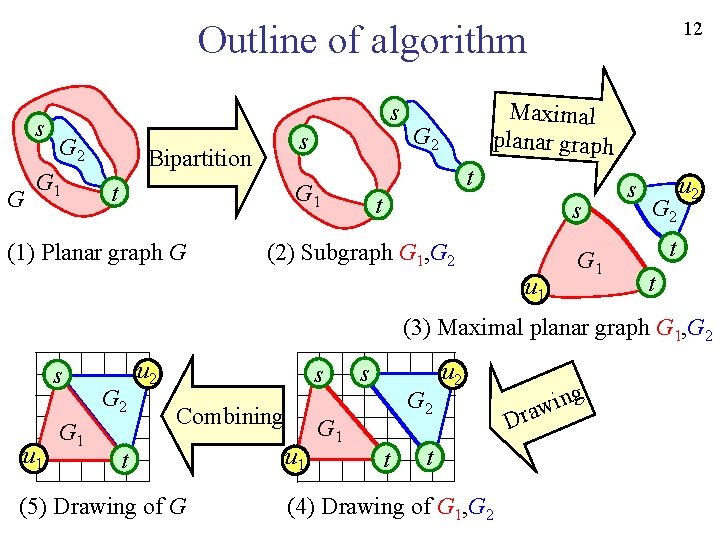
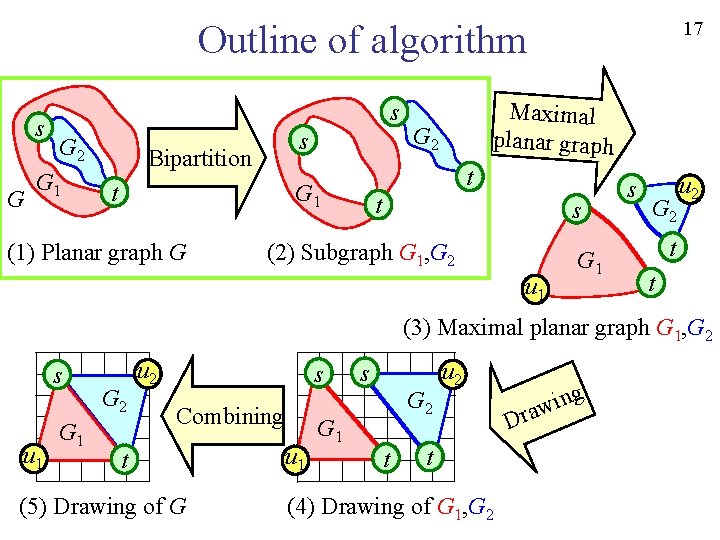
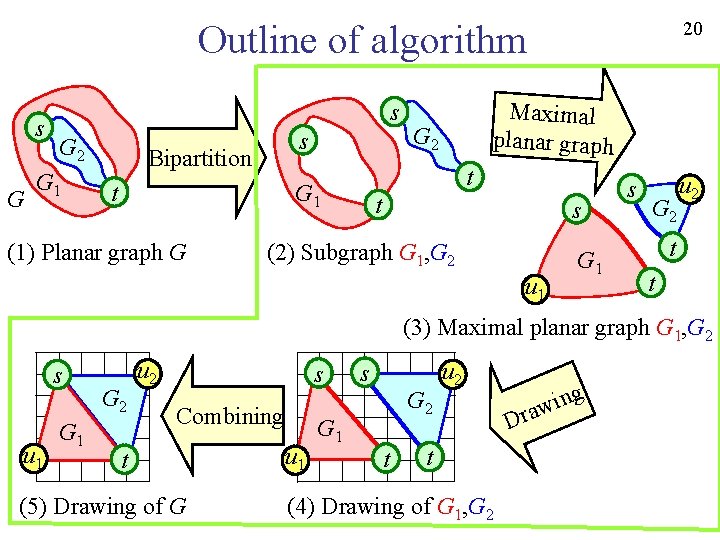
12 Outline of algorithm s G 2 G 1 s Bipartition t G 2 t G 1 (1) Planar graph G Maximal planar graph t s (2) Subgraph G 1, G 2 u 1 G 1 s G 2 u 2 t t (3) Maximal planar graph G 1, G 2 s u 1 G 2 u 2 s Combining t (5) Drawing of G u 1 s G 2 G 1 t u 2 t (4) Drawing of G 1, G 2 g D in w a r

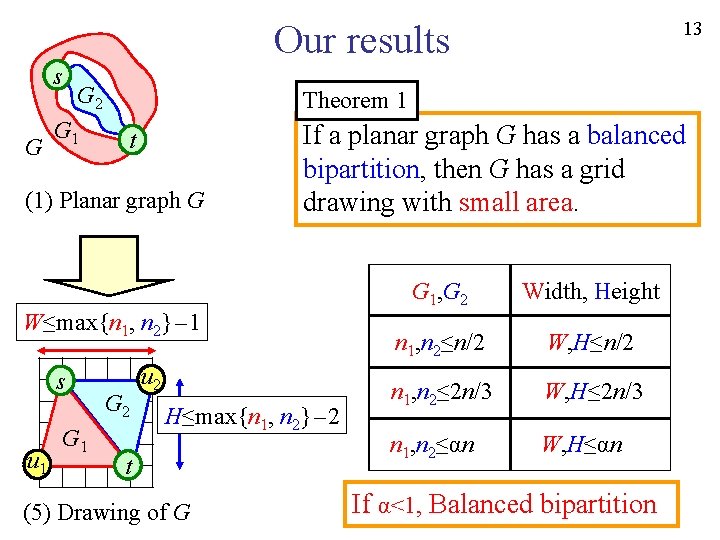
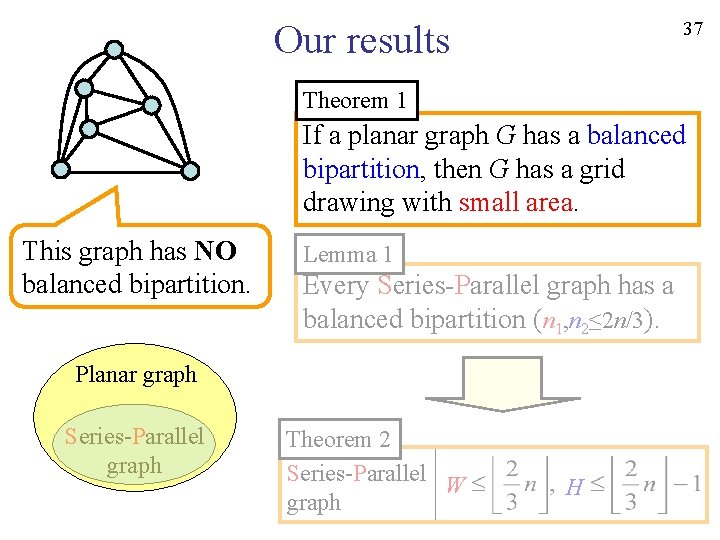
13 Our results s G G 2 G 1 Theorem 1 t (1) Planar graph G If a planar graph G has a balanced bipartition, then G has a grid drawing with small area. W≤max{n 1, n 2}-1 s u 1 G 2 u 2 H≤max{n 1, n 2}-2 t (5) Drawing of G G 1, G 2 Width, Height n 1, n 2≤n/2 W, H≤n/2 n 1, n 2≤ 2 n/3 W, H≤ 2 n/3 n 1, n 2≤αn W, H≤αn If α<1, Balanced bipartition

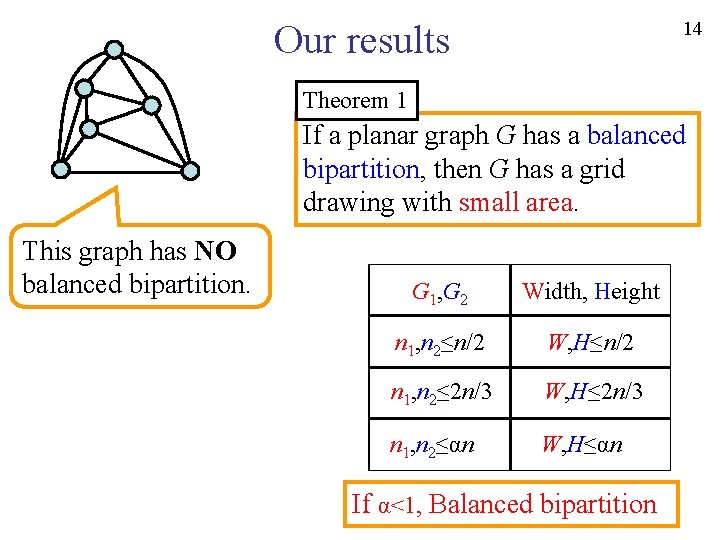
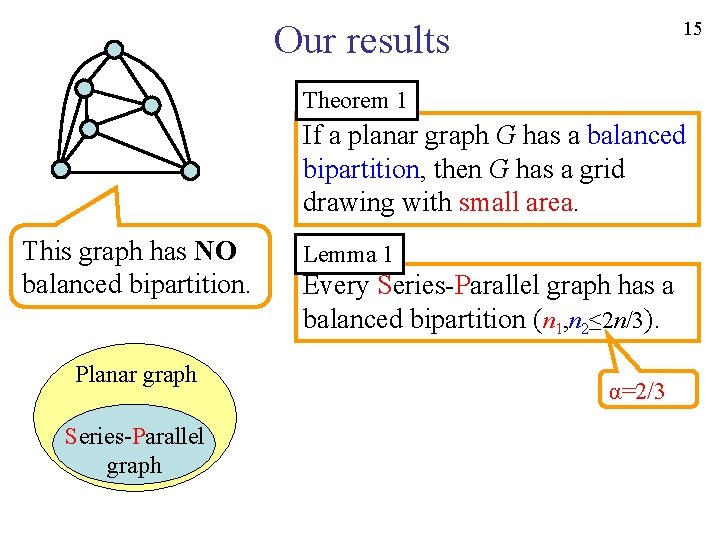
14 Our results Theorem 1 If a planar graph G has a balanced bipartition, then G has a grid drawing with small area. This graph has NO balanced bipartition. G 1, G 2 Width, Height n 1, n 2≤n/2 W, H≤n/2 n 1, n 2≤ 2 n/3 W, H≤ 2 n/3 n 1, n 2≤αn W, H≤αn If α<1, Balanced bipartition

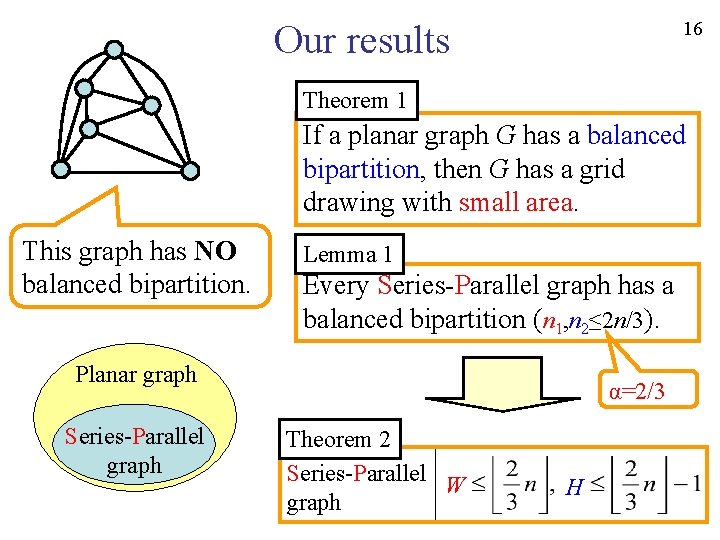
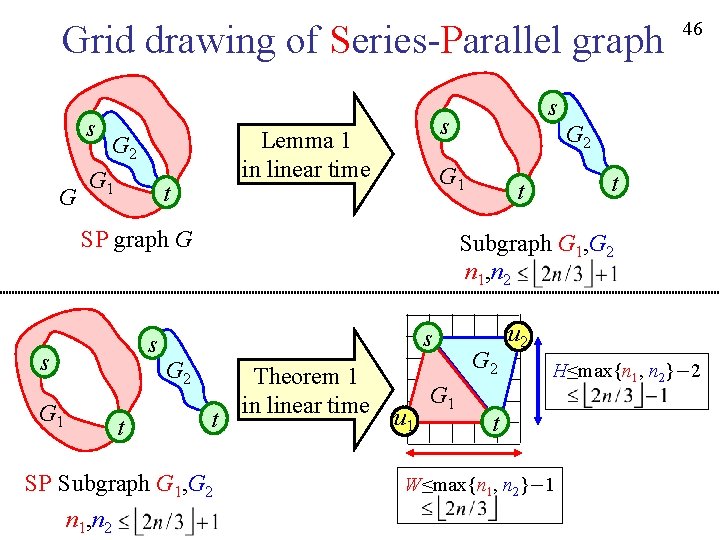
15 Our results Theorem 1 If a planar graph G has a balanced bipartition, then G has a grid drawing with small area. This graph has NO balanced bipartition. Planar graph Series-Parallel graph Lemma 1 Every Series-Parallel graph has a balanced bipartition (n 1, n 2≤ 2 n/3). α=2/3

16 Our results Theorem 1 If a planar graph G has a balanced bipartition, then G has a grid drawing with small area. This graph has NO balanced bipartition. Lemma 1 Every Series-Parallel graph has a balanced bipartition (n 1, n 2≤ 2 n/3). Planar graph Series-Parallel graph α=2/3 Theorem 2 Series-Parallel W graph H

17 Outline of algorithm s G 2 G 1 s Bipartition t G 2 t G 1 (1) Planar graph G Maximal planar graph t s (2) Subgraph G 1, G 2 u 1 G 1 s G 2 u 2 t t (3) Maximal planar graph G 1, G 2 s u 1 G 2 u 2 s Combining t (5) Drawing of G u 1 s G 2 G 1 t u 2 t (4) Drawing of G 1, G 2 g D in w a r

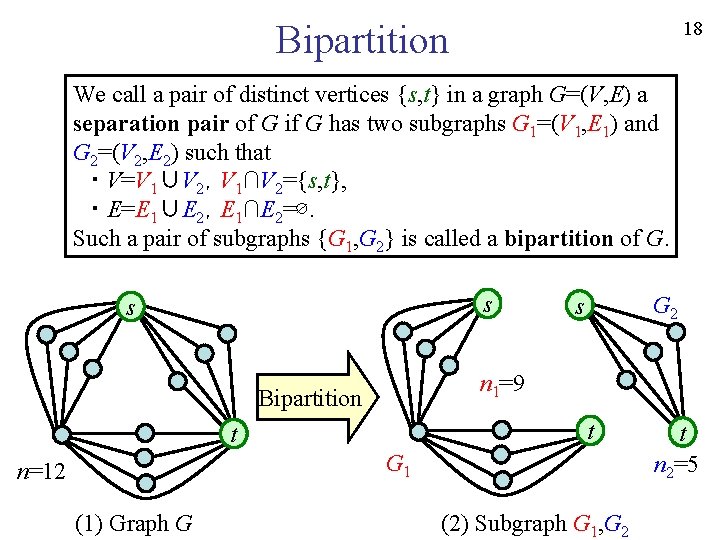
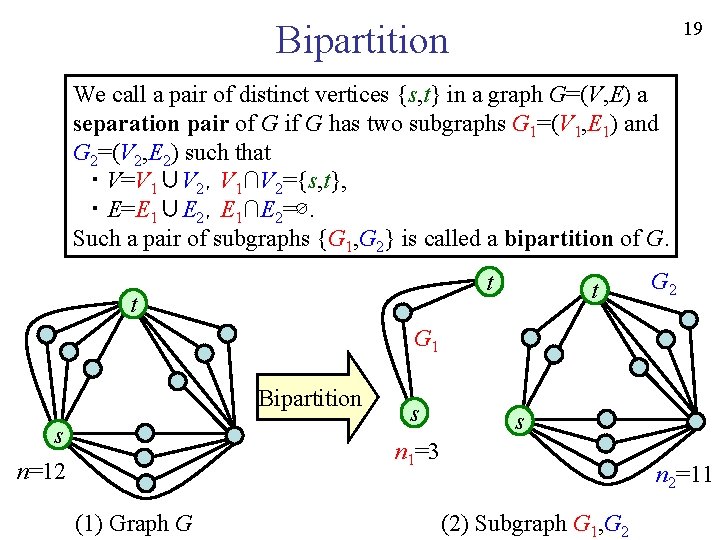
18 Bipartition We call a pair of distinct vertices {s, t} in a graph G=(V, E) a separation pair of G if G has two subgraphs G 1=(V 1, E 1) and G 2=(V 2, E 2) such that ・ V=V 1∪V 2,V 1∩V 2={s, t}, ・ E=E 1∪E 2,E 1∩E 2=∅. Such a pair of subgraphs {G 1, G 2} is called a bipartition of G. s s G 2 s n 1=9 Bipartition t t G 1 n=12 (1) Graph G (2) Subgraph G 1, G 2 t n 2=5

19 Bipartition We call a pair of distinct vertices {s, t} in a graph G=(V, E) a separation pair of G if G has two subgraphs G 1=(V 1, E 1) and G 2=(V 2, E 2) such that ・ V=V 1∪V 2,V 1∩V 2={s, t}, ・ E=E 1∪E 2,E 1∩E 2=∅. Such a pair of subgraphs {G 1, G 2} is called a bipartition of G. t t t G 2 G 1 Bipartition s n=12 s s n 1=3 (1) Graph G n 2=11 (2) Subgraph G 1, G 2

20 Outline of algorithm s G 2 G 1 s Bipartition t G 2 t G 1 (1) Planar graph G Maximal planar graph t s (2) Subgraph G 1, G 2 u 1 G 1 s G 2 u 2 t t (3) Maximal planar graph G 1, G 2 s u 1 G 2 u 2 s Combining t (5) Drawing of G u 1 s G 2 G 1 t u 2 t (4) Drawing of G 1, G 2 g D in w a r

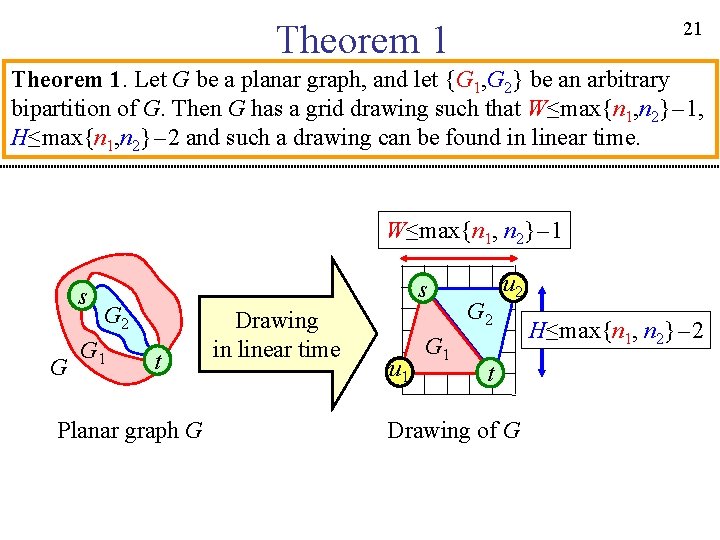
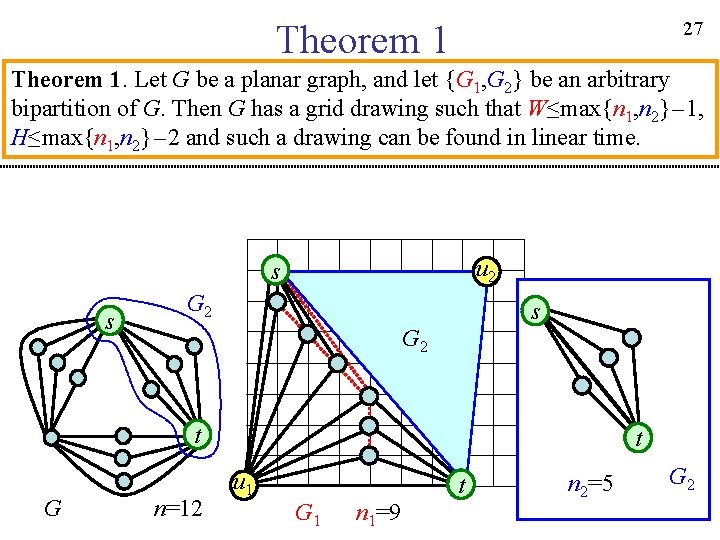
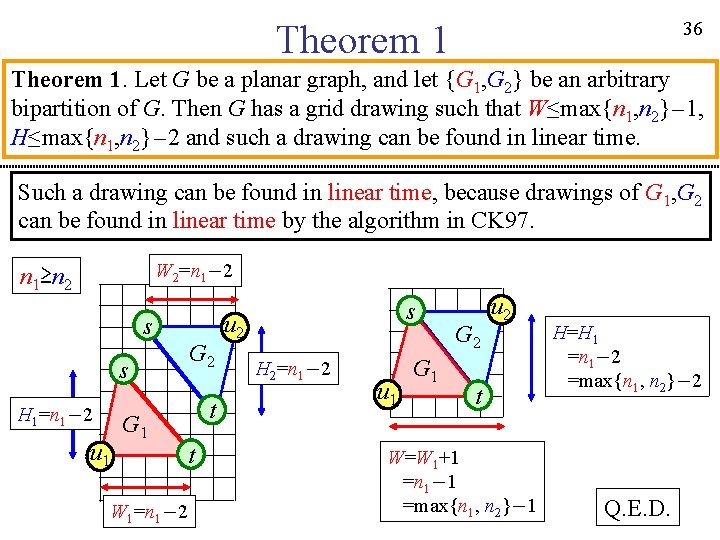
21 Theorem 1. Let G be a planar graph, and let {G 1, G 2} be an arbitrary bipartition of G. Then G has a grid drawing such that W≤max{n 1, n 2}-1, H≤max{n 1, n 2}-2 and such a drawing can be found in linear time. W≤max{n 1, n 2}-1 s G 2 G 1 t Planar graph G Drawing in linear time u 1 G 2 u 2 t Drawing of G H≤max{n 1, n 2}-2

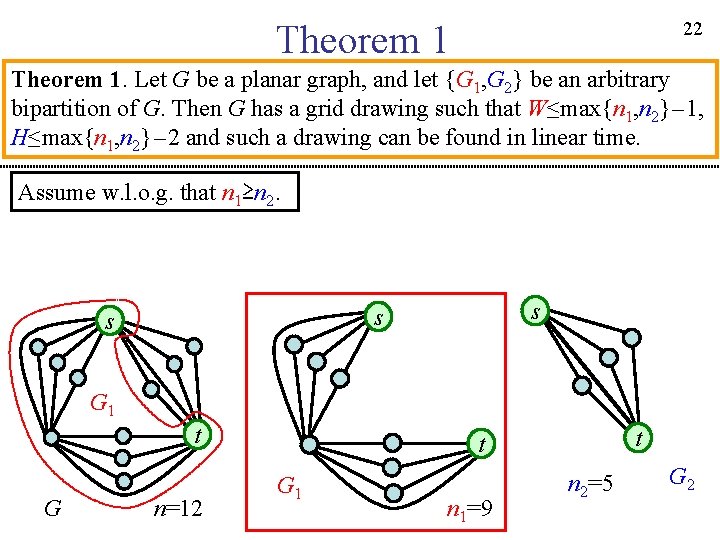
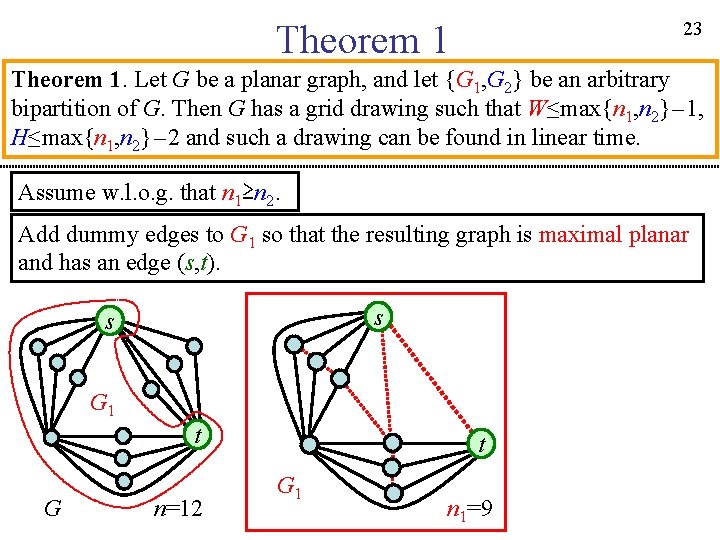
22 Theorem 1. Let G be a planar graph, and let {G 1, G 2} be an arbitrary bipartition of G. Then G has a grid drawing such that W≤max{n 1, n 2}-1, H≤max{n 1, n 2}-2 and such a drawing can be found in linear time. Assume w. l. o. g. that n 1≥n 2. s s s G 1 t G n=12 t t G 1 n 1=9 n 2=5 G 2

23 Theorem 1. Let G be a planar graph, and let {G 1, G 2} be an arbitrary bipartition of G. Then G has a grid drawing such that W≤max{n 1, n 2}-1, H≤max{n 1, n 2}-2 and such a drawing can be found in linear time. Assume w. l. o. g. that n 1≥n 2. Add dummy edges to G 1 so that the resulting graph is maximal planar and has an edge (s, t). s s G 1 t G n=12 t G 1 n 1=9

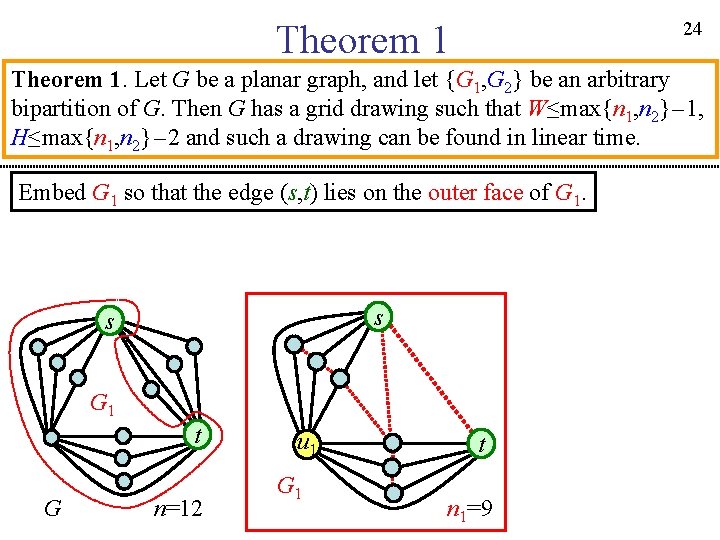
24 Theorem 1. Let G be a planar graph, and let {G 1, G 2} be an arbitrary bipartition of G. Then G has a grid drawing such that W≤max{n 1, n 2}-1, H≤max{n 1, n 2}-2 and such a drawing can be found in linear time. Embed G 1 so that the edge (s, t) lies on the outer face of G 1. s s G 1 t G n=12 u 1 G 1 t n 1=9

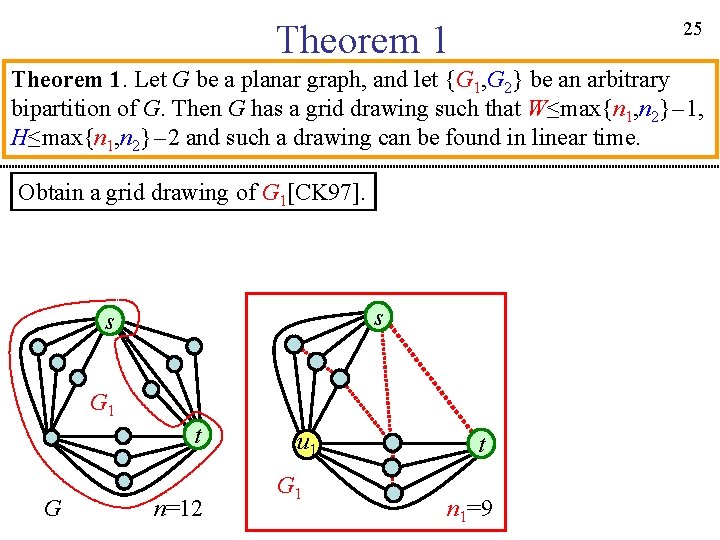
25 Theorem 1. Let G be a planar graph, and let {G 1, G 2} be an arbitrary bipartition of G. Then G has a grid drawing such that W≤max{n 1, n 2}-1, H≤max{n 1, n 2}-2 and such a drawing can be found in linear time. Obtain a grid drawing of G 1[CK 97]. s s G 1 t G n=12 u 1 G 1 t n 1=9

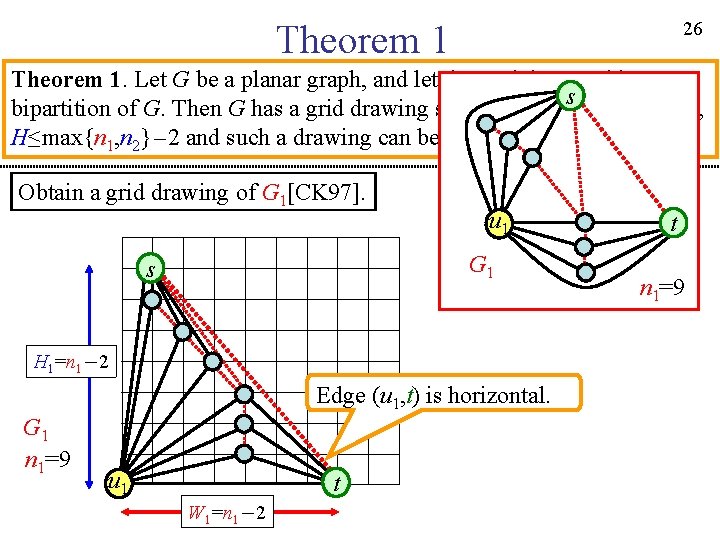
26 Theorem 1. Let G be a planar graph, and let {G 1, G 2} be an arbitrary s bipartition of G. Then G has a grid drawing such that W≤max{n 1, n 2}-1, H≤max{n 1, n 2}-2 and such a drawing can be found in linear time. Obtain a grid drawing of G 1[CK 97]. u 1 G 1 s H 1=n 1-2 Edge (u 1, t) is horizontal. G 1 n 1=9 u 1 t W 1=n 1-2 t n 1=9

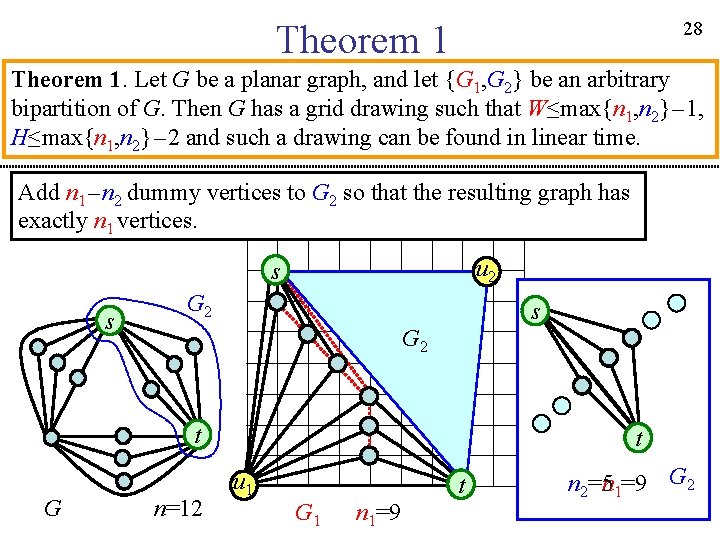
27 Theorem 1. Let G be a planar graph, and let {G 1, G 2} be an arbitrary bipartition of G. Then G has a grid drawing such that W≤max{n 1, n 2}-1, H≤max{n 1, n 2}-2 and such a drawing can be found in linear time. u 2 s s G 2 t G n=12 t u 1 t G 1 n 1=9 n 2=5 G 2

28 Theorem 1. Let G be a planar graph, and let {G 1, G 2} be an arbitrary bipartition of G. Then G has a grid drawing such that W≤max{n 1, n 2}-1, H≤max{n 1, n 2}-2 and such a drawing can be found in linear time. Add n 1-n 2 dummy vertices to G 2 so that the resulting graph has exactly n 1 vertices. u 2 s s G 2 t G n=12 t u 1 t G 1 n 1=9 n 2=5 =n 1=9 G 2

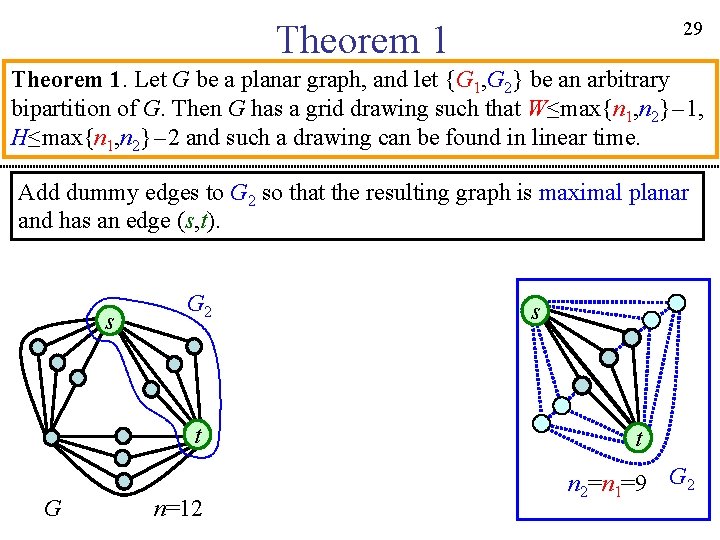
29 Theorem 1. Let G be a planar graph, and let {G 1, G 2} be an arbitrary bipartition of G. Then G has a grid drawing such that W≤max{n 1, n 2}-1, H≤max{n 1, n 2}-2 and such a drawing can be found in linear time. Add dummy edges to G 2 so that the resulting graph is maximal planar and has an edge (s, t). s G 2 t G n=12 s t n 2=n 1=9 G 2

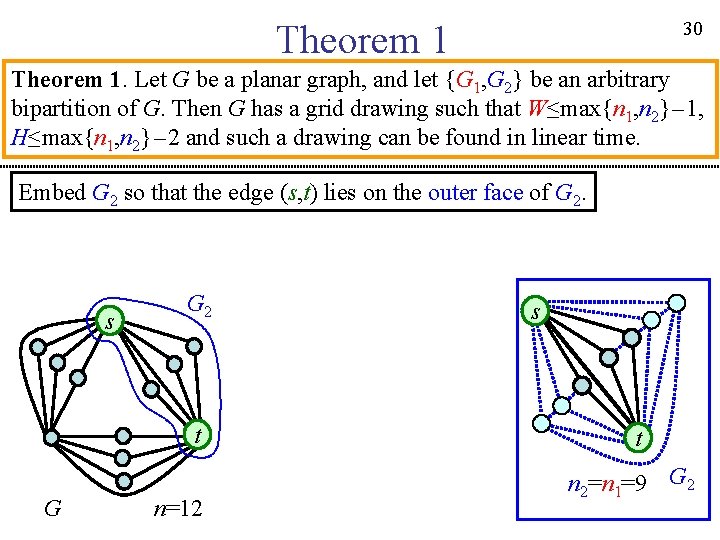
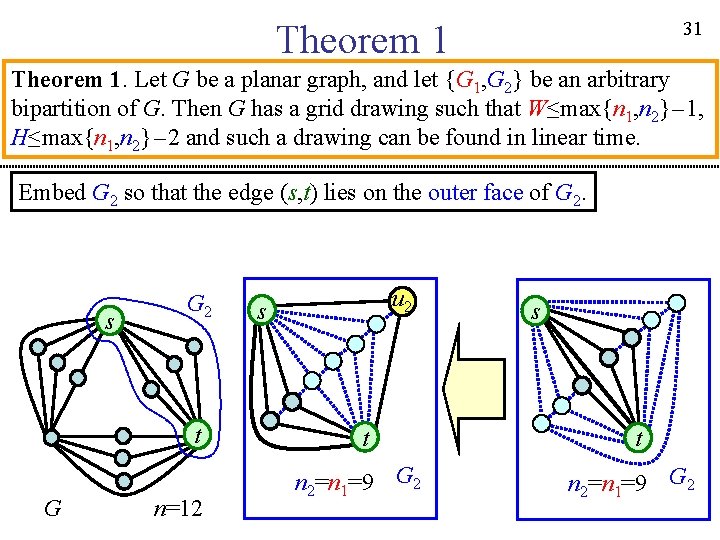
30 Theorem 1. Let G be a planar graph, and let {G 1, G 2} be an arbitrary bipartition of G. Then G has a grid drawing such that W≤max{n 1, n 2}-1, H≤max{n 1, n 2}-2 and such a drawing can be found in linear time. Embed G 2 so that the edge (s, t) lies on the outer face of G 2. s G 2 t G n=12 s t n 2=n 1=9 G 2

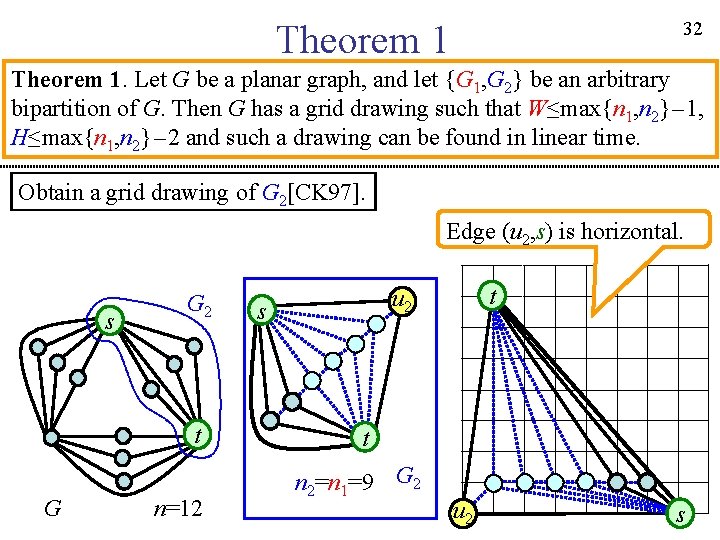
31 Theorem 1. Let G be a planar graph, and let {G 1, G 2} be an arbitrary bipartition of G. Then G has a grid drawing such that W≤max{n 1, n 2}-1, H≤max{n 1, n 2}-2 and such a drawing can be found in linear time. Embed G 2 so that the edge (s, t) lies on the outer face of G 2. s G 2 t G n=12 u 2 s s t t n 2=n 1=9 G 2

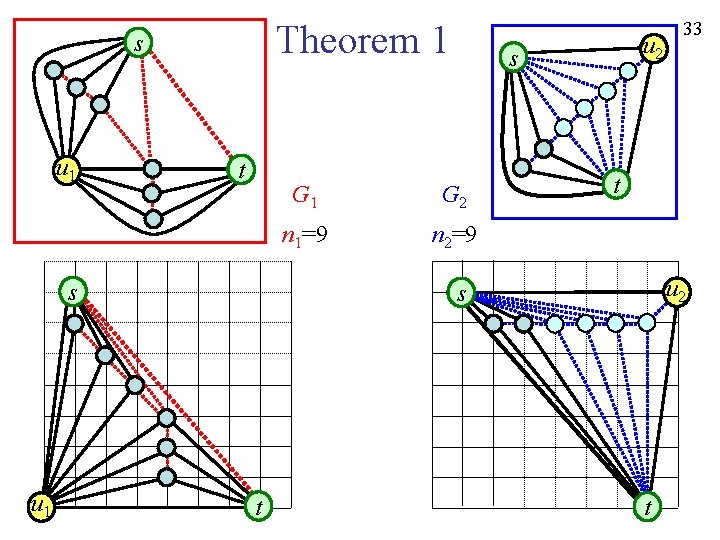
32 Theorem 1. Let G be a planar graph, and let {G 1, G 2} be an arbitrary bipartition of G. Then G has a grid drawing such that W≤max{n 1, n 2}-1, H≤max{n 1, n 2}-2 and such a drawing can be found in linear time. Obtain a grid drawing of G 2[CK 97]. Edge (u 2, s) is horizontal. s G 2 t G n=12 t u 2 s t n 2=n 1=9 G 2 u 2 s

Theorem 1 s u 1 t s u 1 u 2 s G 1 G 2 n 1=9 n 2=9 t u 2 s t 33 t

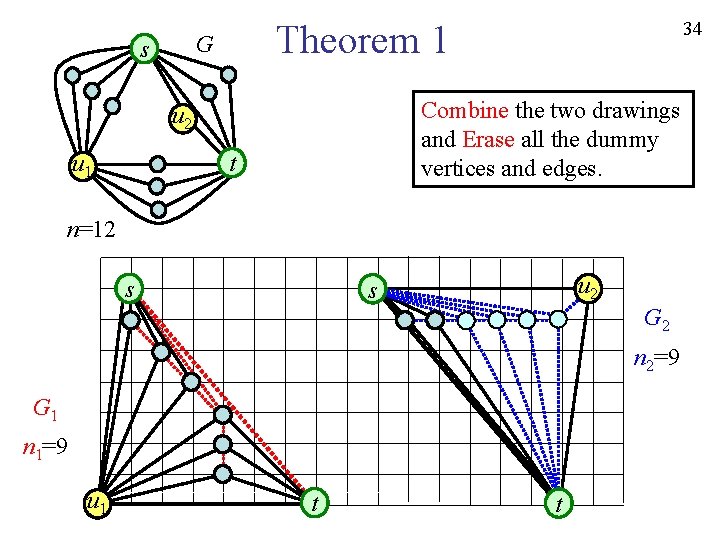
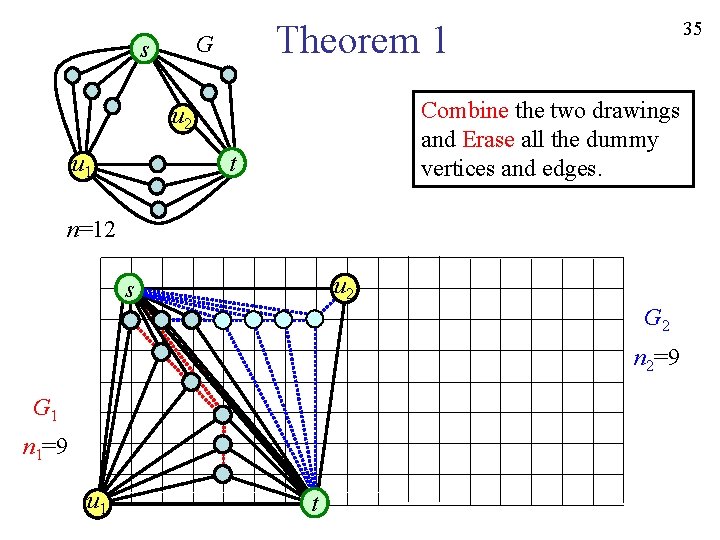
Theorem 1 G s Combine the two drawings and Erase all the dummy vertices and edges. u 2 u 1 34 t n=12 s u 2 s G 2 n 2=9 G 1 n 1=9 u 1 t t

Theorem 1 G s Combine the two drawings and Erase all the dummy vertices and edges. u 2 u 1 35 t n=12 u 2 s G 2 n 2=9 G 1 n 1=9 u 1 t

36 Theorem 1. Let G be a planar graph, and let {G 1, G 2} be an arbitrary bipartition of G. Then G has a grid drawing such that W≤max{n 1, n 2}-1, H≤max{n 1, n 2}-2 and such a drawing can be found in linear time. Such a drawing can be found in linear time, because drawings of G 1, G 2 can be found in linear time by the algorithm in CK 97. W 2=n 1-2 n 1≥n 2 s G 2 s H 1=n 1-2 u 1 t G 1 t W 1=n 1-2 s u 2 H 2=n 1-2 u 1 G 2 u 2 t W=W 1+1 =n 1-1 =max{n 1, n 2}-1 H=H 1 =n 1-2 =max{n 1, n 2}-2 Q. E. D.

37 Our results Theorem 1 If a planar graph G has a balanced bipartition, then G has a grid drawing with small area. This graph has NO balanced bipartition. Lemma 1 Every Series-Parallel graph has a balanced bipartition (n 1, n 2≤ 2 n/3). Planar graph Series-Parallel graph Theorem 2 Series-Parallel W graph H

38 Our results Theorem 1 If a planar graph G has a balanced bipartition, then G has a grid drawing with small area. This graph has NO balanced bipartition. Lemma 1 Every Series-Parallel graph has a balanced bipartition (n 1, n 2≤ 2 n/3). Planar graph Series-Parallel graph Theorem 2 Series-Parallel W graph H

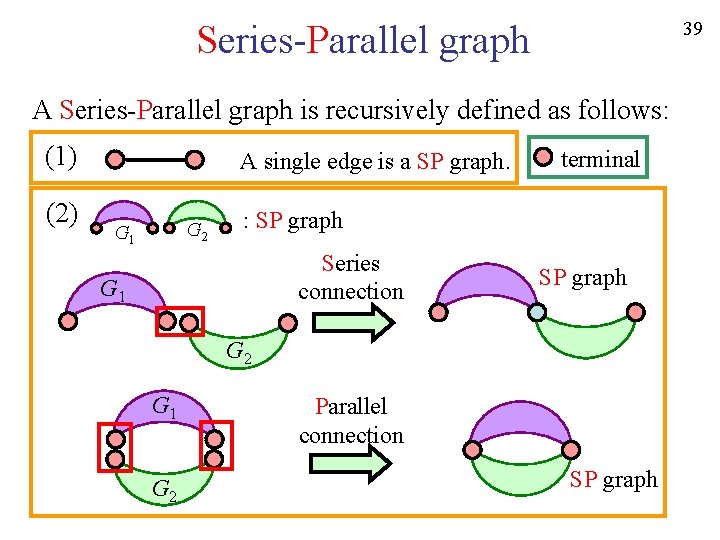
39 Series-Parallel graph A Series-Parallel graph is recursively defined as follows: (1) (2) A single edge is a SP graph. G 2 G 1 terminal : SP graph Series connection G 1 SP graph G 2 G 1 G 2 Parallel connection SP graph

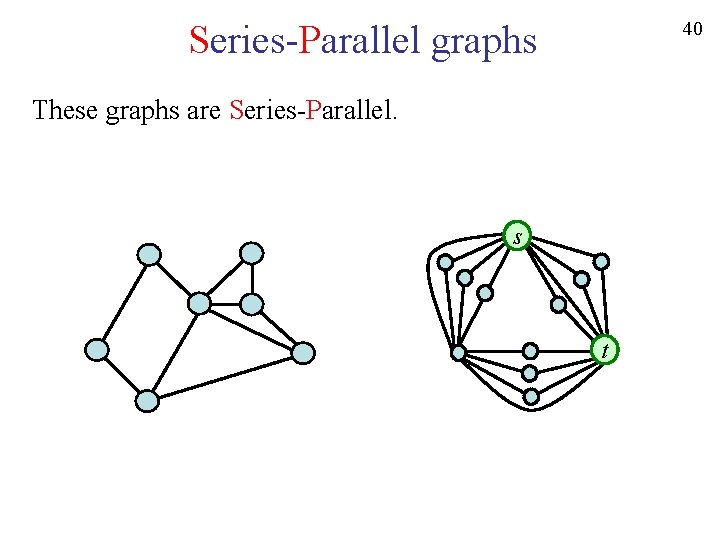
40 Series-Parallel graphs These graphs are Series-Parallel. s t

Bipartition of Series-Parallel graph 41 Lemma 1. Every Series-Parallel graph G of n vertices has a bipartition {G 1, G 2} such that n 1, n 2. Furthermore such a bipartition can be found in linear time. s G G 2 G 1 t SP graph G Bipartition in liner time s s G 1 G 2 t t Subgraph G 1, G 2 n 1, n 2 Suppose for a contradiction that a SP graph has no desired bipartition.

Bipartition of Series-Parallel graph Lemma 1. Every Series-Parallel graph G of n vertices has a bipartition {G 1, G 2} such that n 1, n 2. Furthermore such a bipartition can be found in linear time. Let {s, t} be the most balanced separation pair of G : max{n 1, n 2} is minimum among all bipartitions of G. n 1>2 n/3 G 11 s G 11 G 12 G 1=G 11・G 12 u G 12 G 2 t n 2<n/3 2 -connected SP graph G Assume w. l. o. g. that n 1≥n 2. 42

Bipartition of Series-Parallel graph 43 Lemma 1. Every Series-Parallel graph G of n vertices has a bipartition {G 1, G 2} such that n 1, n 2. Furthermore such a bipartition can be found in linear time. Let {s, t} be the most balanced separation pair of G : max{n 1, n 2} is minimum among all bipartitions of G. n 1>2 n/3 G 1=G 11・G 12 Assume w. l. o. g. that n 1≥n 2 and n 11≥n 12. G 1 n 11>n/3 G 11 n 1> n 11 u G 12 n 1> n 11 G s t 11 n 1> max{n 11, n 11} G 2 Contradiction. n 11<2 n/3 n 1=max{n 1, n 2} n 2<n/3 max{n 1, n 2}> max{n 11, n 11} 2 -connected SP graph G

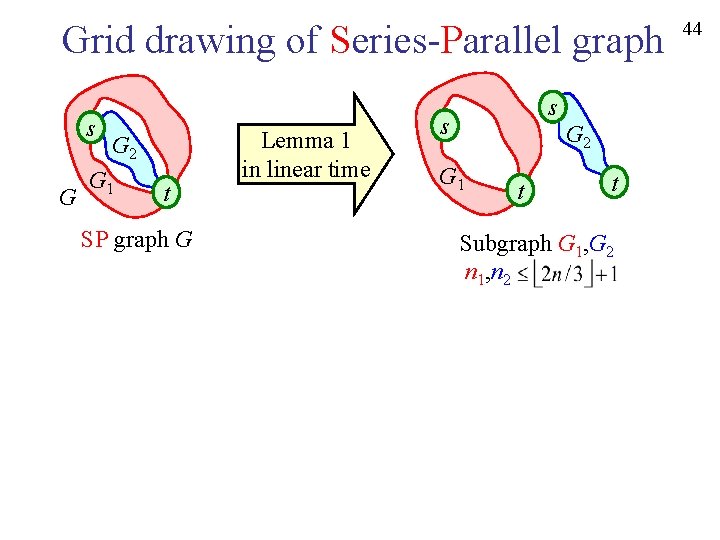
Grid drawing of Series-Parallel graph s G G 2 G 1 t SP graph G Lemma 1 in linear time s s G 2 G 1 t t Subgraph G 1, G 2 n 1, n 2 44

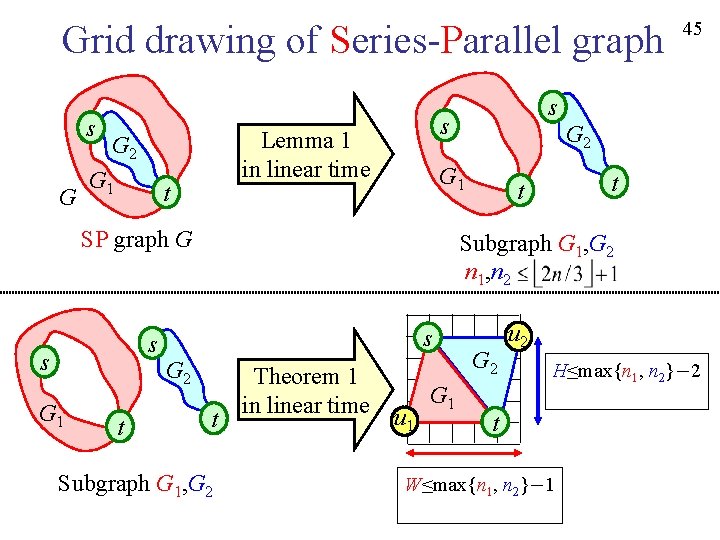
Grid drawing of Series-Parallel graph s G G 1 t s G 2 t t t Subgraph G 1, G 2 n 1, n 2 s G 1 G 2 G 1 SP graph G s s s Lemma 1 in linear time G 2 45 t Subgraph G 1, G 2 Theorem 1 in linear time u 1 G 2 u 2 H≤max{n 1, n 2}-2 t W≤max{n 1, n 2}-1

Grid drawing of Series-Parallel graph s G G 1 t t Subgraph G 1, G 2 n 1, n 2 s s G 2 t G 2 G 1 SP graph G s s s Lemma 1 in linear time G 2 46 t SP Subgraph G 1, G 2 n 1, n 2 Theorem 1 in linear time u 1 G 2 u 2 H≤max{n 1, n 2}-2 t W≤max{n 1, n 2}-1

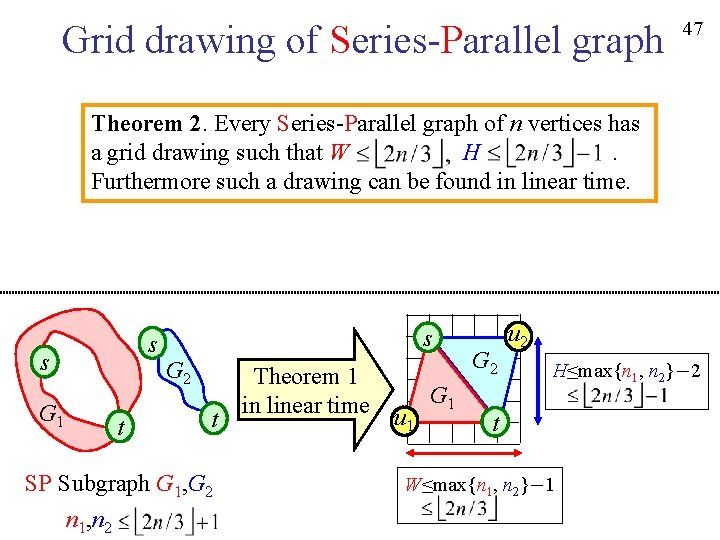
Grid drawing of Series-Parallel graph 47 Theorem 2. Every Series-Parallel graph of n vertices has a grid drawing such that W H. Furthermore such a drawing can be found in linear time. s G 1 s s G 2 t t SP Subgraph G 1, G 2 n 1, n 2 Theorem 1 in linear time u 1 G 2 u 2 H≤max{n 1, n 2}-2 t W≤max{n 1, n 2}-1

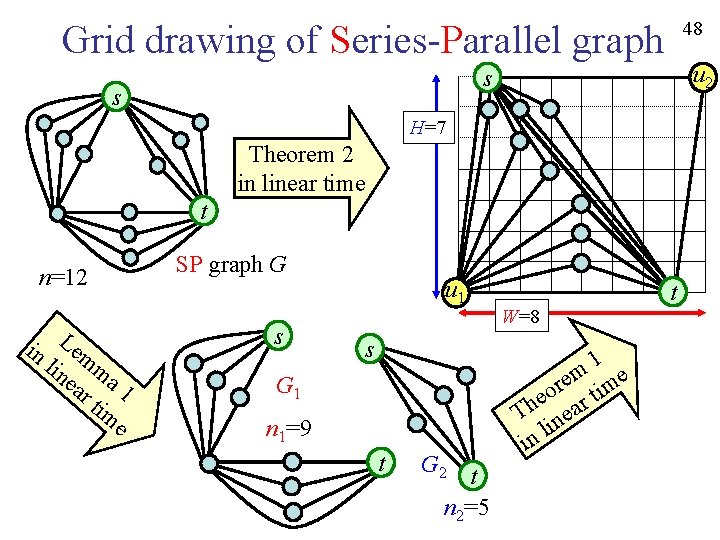
48 Grid drawing of Series-Parallel graph u 2 s s H=7 Theorem 2 in linear time t n=12 in Lem lin m ea a 1 rt im e SP graph G s u 1 s G 1 n 1=9 t G 2 t n 2=5 W=8 1 m re time o e ar h T ne li n i t

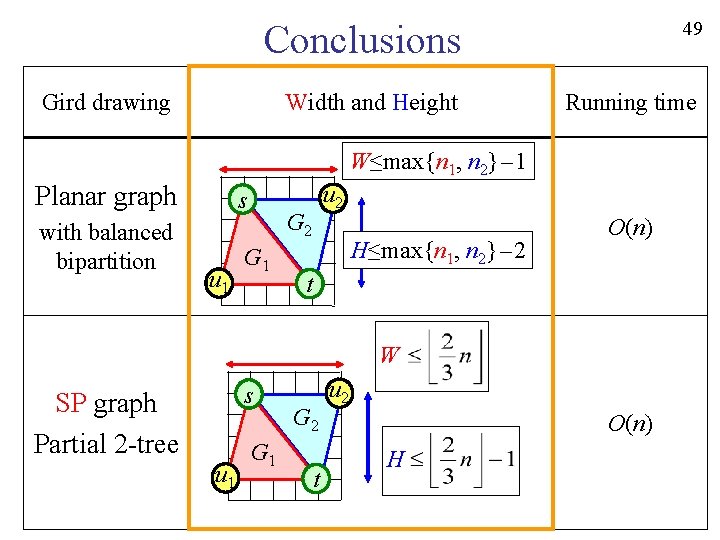
49 Conclusions Gird drawing Width and Height Running time W≤max{n 1, n 2}-1 Planar graph with balanced bipartition s u 1 u 2 G 1 H≤max{n 1, n 2}-2 O(n) t W s SP graph Partial 2 -tree u 1 G 2 t u 2 O(n) H

50
 Micro vector
Micro vector Habitos de la victoria privada
Habitos de la victoria privada Yep 10
Yep 10 Priority of sendai framework
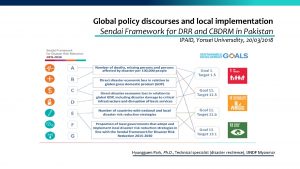
Priority of sendai framework Priority of sendai framework
Priority of sendai framework Priority of sendai framework
Priority of sendai framework Mediateca de sendai
Mediateca de sendai Sendai framework philippines
Sendai framework philippines Diferencia entre el marco de hyogo y sendai
Diferencia entre el marco de hyogo y sendai Hyogo çerçeve planı
Hyogo çerçeve planı 7 metas globales del marco de sendai
7 metas globales del marco de sendai Sendai
Sendai Marco de sendai
Marco de sendai Victoria and albert ward st mary's hospital
Victoria and albert ward st mary's hospital The latin american city model
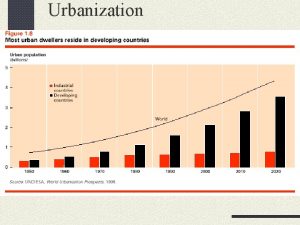
The latin american city model Inner city suburbs
Inner city suburbs Is mexico city a primate city
Is mexico city a primate city Uniting homeshare program
Uniting homeshare program Queen victoria age 18
Queen victoria age 18 Vcaa eal curriculum
Vcaa eal curriculum Victoria ocampo francisca ocampo
Victoria ocampo francisca ocampo Victoria nyanza sailing club
Victoria nyanza sailing club Victoria mulhern
Victoria mulhern Omer boyaci
Omer boyaci Victoria climbe
Victoria climbe Queen victoria age 18
Queen victoria age 18 Nangam kalima
Nangam kalima Victoria selby
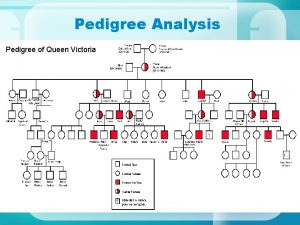
Victoria selby Queen victoria family tree hemophilia
Queen victoria family tree hemophilia Victoria peditree
Victoria peditree Victoria map outline
Victoria map outline Yo me llamo victoria
Yo me llamo victoria Guadalupe victoria linea del tiempo
Guadalupe victoria linea del tiempo Ewa strzelczyk
Ewa strzelczyk Salmo cantare al señor sublime su victoria
Salmo cantare al señor sublime su victoria Victoria lindon
Victoria lindon Elapsed time mountains hills rocks
Elapsed time mountains hills rocks Is the victorian era named after queen victoria
Is the victorian era named after queen victoria Victoria climbi
Victoria climbi Cantare al señor sublime es su victoria
Cantare al señor sublime es su victoria Victoria allgar
Victoria allgar Vic abbreviation
Vic abbreviation Victoria waite
Victoria waite Victorian curriculum history
Victorian curriculum history Stem curriculum victoria
Stem curriculum victoria Victoria purcell gates
Victoria purcell gates Tnm ovario
Tnm ovario Caring for animals clipart
Caring for animals clipart Altura management
Altura management Dance curriculum victoria
Dance curriculum victoria Victoria haddad
Victoria haddad