VERJETNOST IN STATISTIKA POVPRENA VREDNOST IN RAZPRENOST NEKATERIH










- Slides: 12

VERJETNOST IN STATISTIKA POVPREČNA VREDNOST IN RAZPRŠENOST NEKATERIH POMEMBNIH PORAZDELITEV E(X)=n. p D(X)=n. p. q E(X)=a D(X)=a MATEMATIKA 2 1

VERJETNOST IN STATISTIKA POVPREČNA VREDNOST IN RAZPRŠENOST E(X)=a =0 (liha funkcija) =1 =0 =1 D(X)= 2 (X)= MATEMATIKA 2 2

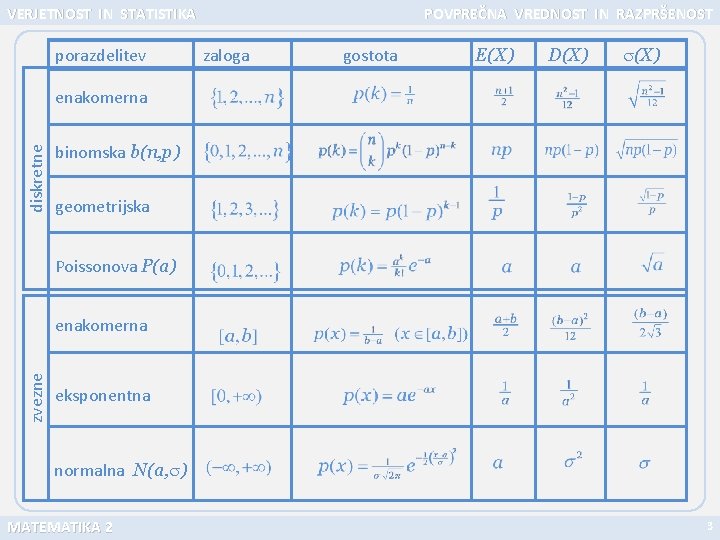
VERJETNOST IN STATISTIKA porazdelitev POVPREČNA VREDNOST IN RAZPRŠENOST zaloga gostota E(X) D(X) diskretne enakomerna binomska b(n, p) geometrijska Poissonova P(a) zvezne enakomerna eksponentna normalna N(a, ) MATEMATIKA 2 3

VERJETNOST IN STATISTIKA SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovanec vržemo trikrat. Z X označimo število grbov pri prvem metu (0 ali 1), z Y pa skupno število grbov (0, 1, 2 ali 3). Kako sta spremenljivki X in Y odvisni druga od druge? Vpeljemo skupno porazdelitev dveh slučajnih spremenljivk pi, j=p(xi, yj)=P(X=xi, Y=yj) Možni izidi so {ggg, ggc, gcg, cgg, gcc, cgc, ccg, ccc}, zato dobimo Vsota tabele po vrsticah je porazdelitev spremenljivke X, vsota po stolpcih pa je porazdelitev spremenljivke Y. Diskretna porazdelitev (X, Y) z gostoto p(xi, yj) Zvezna porazdelitev (X, Y) z gostoto p(x, y) (X, Y) zvezno porazdeljena MATEMATIKA 2 4

VERJETNOST IN STATISTIKA SKUPNE PORAZDELITVE FUNKCIJE VEČ SLUČAJNIH SPREMENLJIVK Posebej: MATEMATIKA 2 5

VERJETNOST IN STATISTIKA SKUPNE PORAZDELITVE NEODVISNOST SLUČAJNIH SPREMENLJIVK Slučajni spremenljivki X in Y sta neodvisni, če sta dogodka P(X ≤ x) in P(Y ≤ y) neodvisna za vse pare x, y. Ekvivalentno: P(X ≤ x, Y ≤ y)=P(X ≤ x). P(Y ≤ y) ali F(x, y)=FX(x). FY(y) p(x, y)=p. X(x). p. Y(y) ali za poljubna x, y. Naj bo X porazdeljena po N(0, 1) in naj bo Y=X 2 MATEMATIKA 2 6

VERJETNOST IN STATISTIKA SKUPNE PORAZDELITVE KOVARIANCA X, Y sta nekorelirana, če je K(X, Y)=0 X, Y neodvisna ⇒ X, Y nekorelirana ⇔ D(X+Y)=D(X)+D(Y) X in Y sta korelirana (in torej tudi odvisna) MATEMATIKA 2 7

VERJETNOST IN STATISTIKA MATEMATIKA 2 SKUPNE PORAZDELITVE 8

VERJETNOST IN STATISTIKA ZAKONI VELIKIH ŠTEVIL Igralec zadane v povprečju 70% metov na koš. Kaj je bolj verjetno: da bo v 10 metih zadel 10 -krat ali da bo v 100 metih zadel več kot 80 -krat? Prva možnost je trikrat (!) bolj verjetna. Zakaj je tako? Zakon velikih števil: z večanjem števila poskusov se zmanjšuje verjetnost odklona od povprečja. POMEN STANDARDNEGA ODKLONA Naj bo X slučajna spremenljivka z gostoto p(x), povprečjem m=E(X) in odklonom = (X). ocena Čebiševa P(|X-E(X)| ≥ 2 ) ≤ 0. 25 ocena velja za poljubno porazdelitev za primerjavo: pri normalni porazdelitvi je P(|X-E(X)| ≥ 2 ) ≤ 0. 05 MATEMATIKA 2 9

VERJETNOST IN STATISTIKA ZAKONI VELIKIH ŠTEVIL Pri n neodvisnih ponovitev nekega poskusa lahko izide gledamo kot zaporedje neodvisnih in enako porazdeljenih slučajnih spremenljivk X 1, X 2, . . . Xn. povprečje izidov Porazdelitev spremenljivke Sn je zapletena. n-krat vržemo kocko, Xk je število pik pri k-tem metu n-krat vržemo žogo na koš, Xk je število pik zadetkov (0 ali 1) pri k-tem metu pri metu kocke ima Sn 5 n+1 izidov, z različnimi verjetnostmi pri metu na koš je Sn relativna frekvenca zadetkov, porazdelitev je binomska Privzemimo, da so X 1, X 2, . . . Xn nekorelirane in enako porazdeljene (kot spremenljivka X). E(Sn)=E(X) Z naraščanjem števila poskusov pada razpršenost povprečja izidov proti 0. MATEMATIKA 2 10

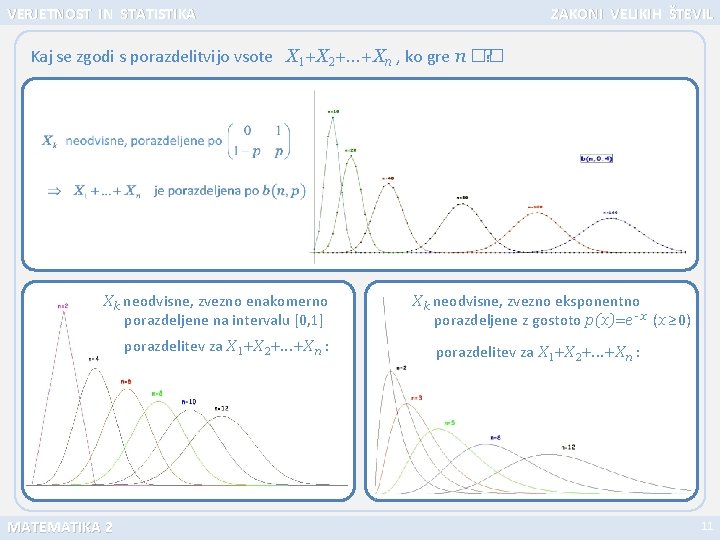
VERJETNOST IN STATISTIKA ZAKONI VELIKIH ŠTEVIL Kaj se zgodi s porazdelitvijo vsote X 1+X 2+. . . +Xn , ko gre n �� ? Xk neodvisne, zvezno enakomerno porazdeljene na intervalu [0, 1] porazdelitev za X 1+X 2+. . . +Xn : MATEMATIKA 2 Xk neodvisne, zvezno eksponentno porazdeljene z gostoto p(x)=e - x (x ≥ 0) porazdelitev za X 1+X 2+. . . +Xn : 11

VERJETNOST IN STATISTIKA ZAKONI VELIKIH ŠTEVIL Porazdelitve X 1+X 2+. . . +Xn zavzamejo zvonasto obliko, vendar jih težko primerjamo ker se ‘premikajo’. Rešitev: vsoto standardiziramo. X 1, X 2, X 3, . . . neodvisne, enako porazdeljene slučajne spremenljivke s povprečjem a in standardnim odklonom � ; Centralni limitni izrek: standardizirana porazdelitev vsote konvergira proti standardni normalni porazdelitvi Neko količino merimo z metodo, ki ima standarno napako (tj. standardni odklon od merjene vrednosti) enako . Opravimo 20 neodvisnih meritev in vzamemo njihovo povprečje. Kolikšna je verjetnost, da se to povprečje razlikuje od merjene količine za več kot /2? Posamezne meritve gledamo kot slučajne spremenljivke: X 1, X 2, . . . , X 20 Po zakonu velikih števil lahko privzamemo E(Xi)=m (merjena količina), obenem je (Xi)= Ocena, ki jo dobimo iz centralnega limitnega izreka je veliko natančnejša. MATEMATIKA 2 12
 Pogojna verjetnost
Pogojna verjetnost Istorija srpskog novca
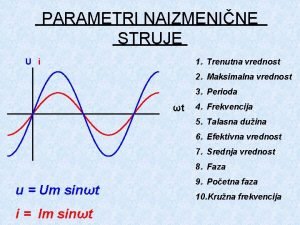
Istorija srpskog novca Trenutna vrednost struje
Trenutna vrednost struje Porez na dodatu vrednost definicija
Porez na dodatu vrednost definicija Srednje vrednosti
Srednje vrednosti Afekciona vrednost stvari
Afekciona vrednost stvari Neto sadasnja vrednost
Neto sadasnja vrednost Istinitosna vrednost iskaza
Istinitosna vrednost iskaza Brokoli hranilna vrednost
Brokoli hranilna vrednost Reciprocna vrednost
Reciprocna vrednost Pokazatelji efikasnosti
Pokazatelji efikasnosti Vremenska vrednost novca
Vremenska vrednost novca Celobrojna vrednost
Celobrojna vrednost