Utility Molly W Dahl Georgetown University Econ 101

Utility Molly W. Dahl Georgetown University Econ 101 – Spring 2009 1

Utility Functions A utility function U(x) represents a preference relation f if and only if: ~ p n x’ x” U(x’) > U(x”) x’ p x” U(x’) < U(x”) x’ ~ x” U(x’) = U(x”). 2

Utility Functions Utility is an ordinal concept. n E. g. if U(x) = 6 and U(y) = 2 then bundle x is strictly preferred to bundle y. But x is not preferred three times as much as is y. n ¨ The magnitude of the difference does not matter, only the order. 3

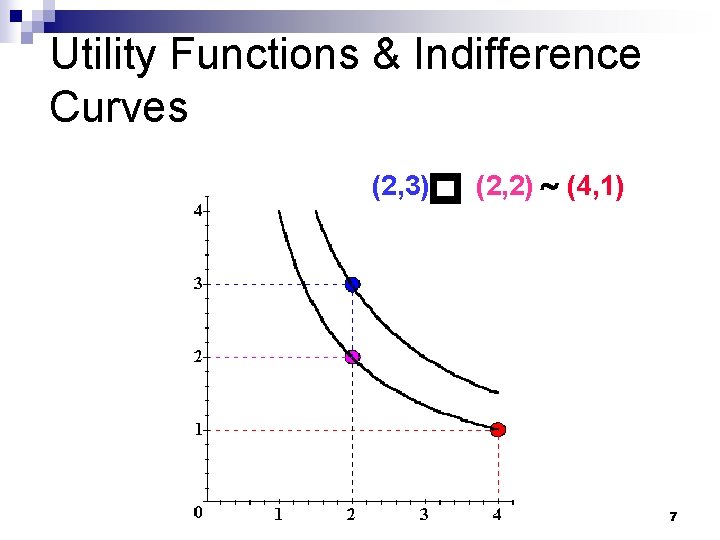
Utility Functions & Indifference Curves Consider the bundles (4, 1), (2, 3) and (2, 2). n Suppose (2, 3) (4, 1) ~ (2, 2). n Assign to these bundles any numbers that preserve the preference ordering; e. g. U(2, 3) = 6 > U(4, 1) = U(2, 2) = 4. n Call these numbers utility levels. n p 4

Utility Functions & Indifference Curves n An indifference curve contains equally preferred bundles. Equal preference same utility level. n Therefore, all bundles in an indifference curve have the same utility level. n 5

Utility Functions & Indifference Curves So the bundles (4, 1) and (2, 2) are in the indiff. curve with utility level U º 4 n But the bundle (2, 3) is in the indiff. curve with utility level U º 6. n On an indifference curve diagram, this preference information looks as follows: n 6

Utility Functions & Indifference Curves p x 2 (2, 3) (2, 2) ~ (4, 1) Uº 6 Uº 4 x 1 7

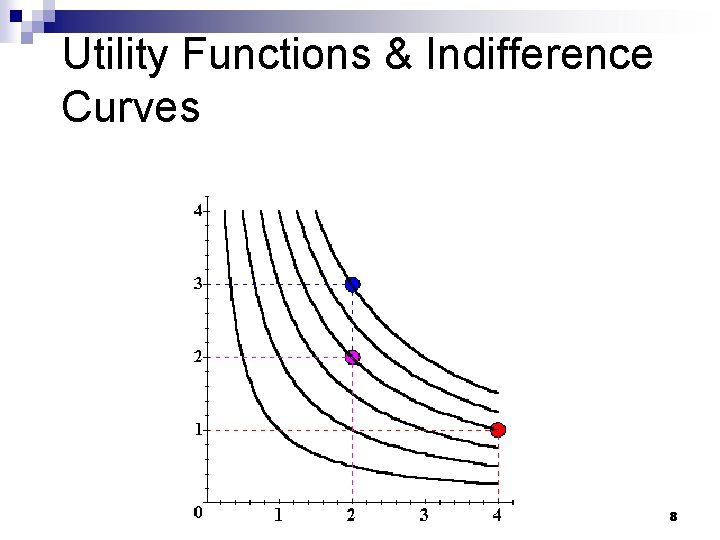
Utility Functions & Indifference Curves x 2 Uº 6 Uº 4 Uº 2 x 1 8

Utility Functions & Indifference Curves Comparing all possible consumption bundles gives the complete collection of the consumer’s indifference curves, each with its assigned utility level. n This complete collection of indifference curves completely represents the consumer’s preferences. n 9

Utility Functions & Indifference Curves The collection of all indifference curves for a given preference relation is an indifference map. n An indifference map is equivalent to a utility function; each is the other. n 10

Utility Functions There is no unique utility function representation of a preference relation. n Suppose U(x 1, x 2) = x 1 x 2 represents a preference relation. n Again consider the bundles (4, 1), (2, 3) and (2, 2). n 11

Utility Functions U(x 1, x 2) = x 1 x 2, so U(2, 3) = 6 > U(4, 1) = U(2, 2) = 4; that is, (2, 3) p n (4, 1) ~ (2, 2). 12

Utility Functions (2, 3) p U(x 1, x 2) = x 1 x 2 n Define V = U 2. n (4, 1) ~ (2, 2). 13

Utility Functions U(x 1, x 2) = x 1 x 2 (2, 3) (4, 1) ~ (2, 2). n Define V = U 2. n Then V(x 1, x 2) = x 12 x 22 and V(2, 3) = 36 > V(4, 1) = V(2, 2) = 16 so again (2, 3) (4, 1) ~ (2, 2). n V preserves the same order as U and so represents the same preferences. p n p 14

Utility Functions p U(x 1, x 2) = x 1 x 2 (2, 3) n Define W = 2 U + 10. n (4, 1) ~ (2, 2). 15

Utility Functions U(x 1, x 2) = x 1 x 2 (2, 3) (4, 1) ~ (2, 2). n Define W = 2 U + 10. n Then W(x 1, x 2) = 2 x 1 x 2+10 so W(2, 3) = 22 > W(4, 1) = W(2, 2) = 18. Again, (2, 3) (4, 1) ~ (2, 2). n W preserves the same order as U and V and so represents the same preferences. p n p 16

Utility Functions If ¨U is a utility function that represents a preference relation f and ~ ¨ f is a strictly increasing function, Then V = f(U) is also a utility function representing f. ~ ¨ That is, utility functions are unique up to a monotone transformation 17

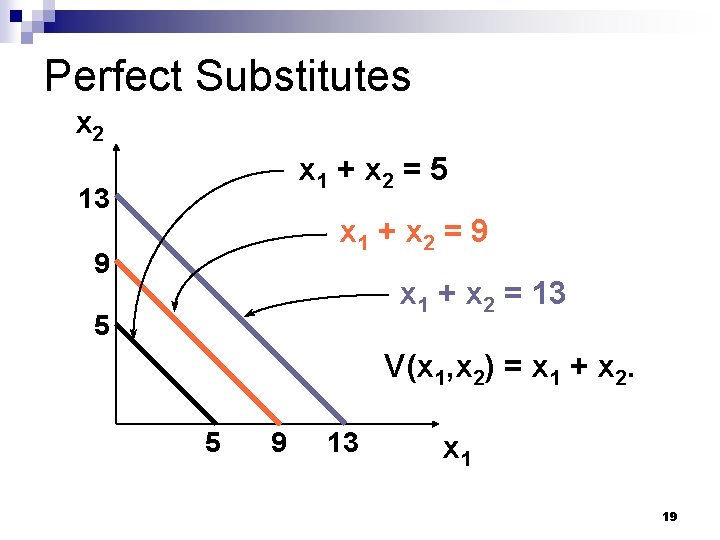
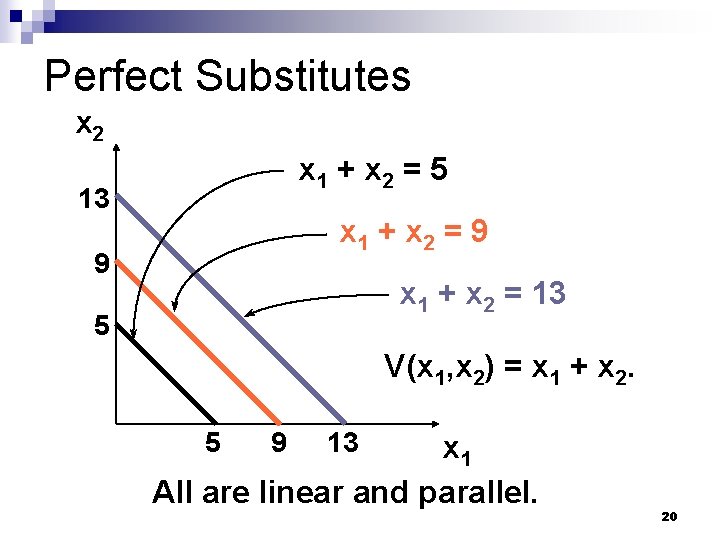
Some Other Utility Functions and Their Indifference Curves n Consider V(x 1, x 2) = x 1 + x 2. What do the indifference curves for this utility function look like? (note: only the total amount of the two commodities determines the utility) 18

Perfect Substitutes x 2 x 1 + x 2 = 5 13 x 1 + x 2 = 9 9 x 1 + x 2 = 13 5 V(x 1, x 2) = x 1 + x 2. 5 9 13 x 1 19

Perfect Substitutes x 2 x 1 + x 2 = 5 13 x 1 + x 2 = 9 9 x 1 + x 2 = 13 5 V(x 1, x 2) = x 1 + x 2. 5 9 13 x 1 All are linear and parallel. 20

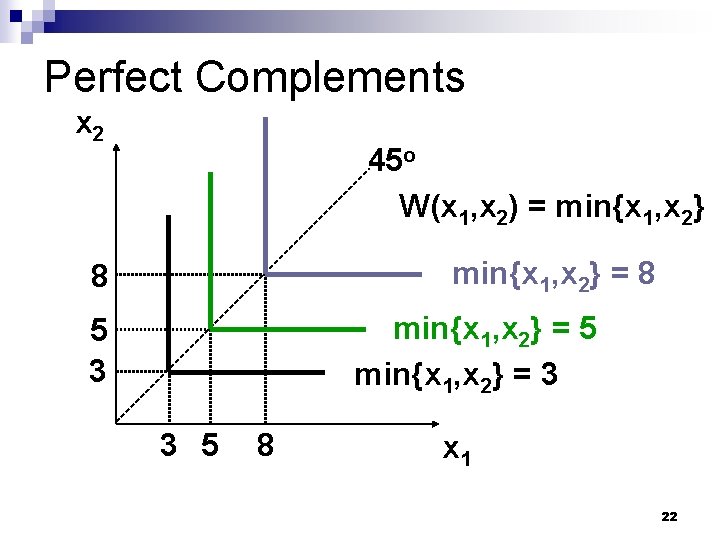
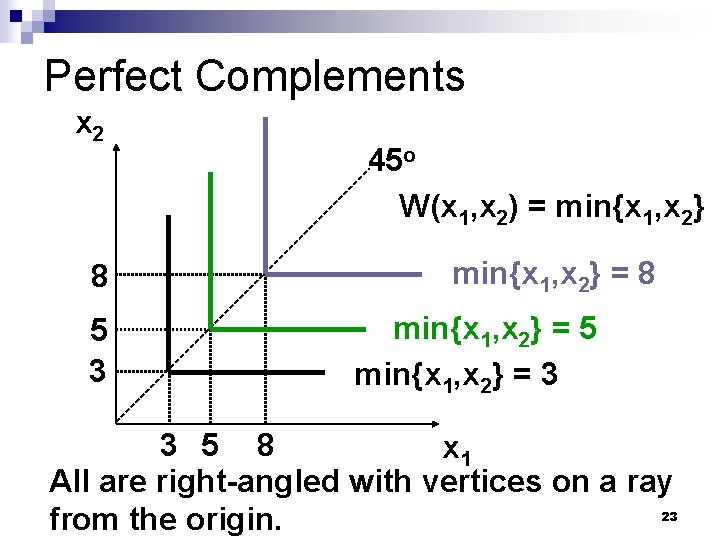
Some Other Utility Functions and Their Indifference Curves n Consider W(x 1, x 2) = min{x 1, x 2}. What do the indifference curves for this utility function look like? (note: only the number of pairs matter) 21

Perfect Complements x 2 45 o W(x 1, x 2) = min{x 1, x 2} = 8 8 min{x 1, x 2} = 5 min{x 1, x 2} = 3 5 3 3 5 8 x 1 22

Perfect Complements x 2 8 5 3 45 o W(x 1, x 2) = min{x 1, x 2} = 8 min{x 1, x 2} = 5 min{x 1, x 2} = 3 3 5 8 x 1 All are right-angled with vertices on a ray from the origin. 23

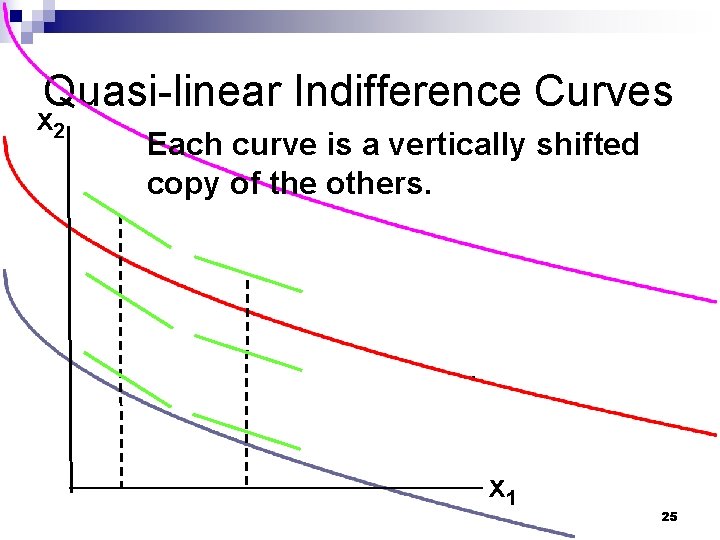
Some Other Utility Functions and Their Indifference Curves n A utility function of the form U(x 1, x 2) = f(x 1) + x 2 is linear in just x 2 and is called quasilinear. n E. g. U(x 1, x 2) = 2 x 11/2 + x 2. 24

Quasi-linear Indifference Curves x 2 Each curve is a vertically shifted copy of the others. x 1 25

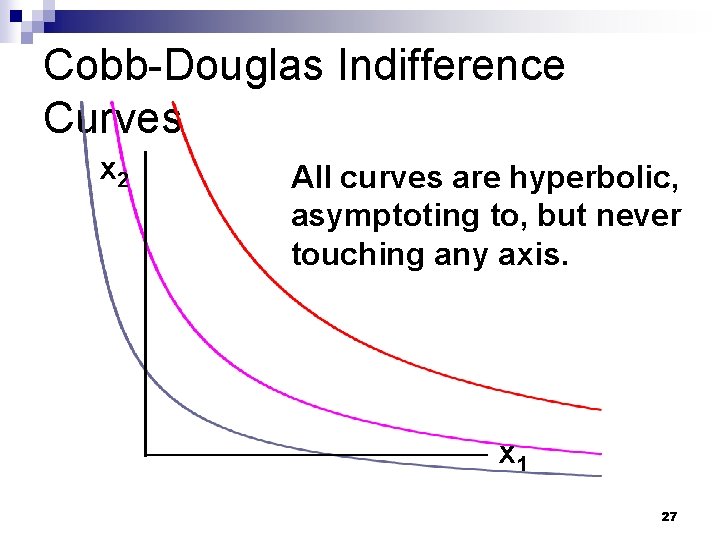
Some Other Utility Functions and Their Indifference Curves n Any utility function of the form U(x 1, x 2) = x 1 a x 2 b with a > 0 and b > 0 is called a Cobb. Douglas utility function. n E. g. U(x 1, x 2) = x 11/2 x 21/2 (a = b = 1/2) V(x 1, x 2) = x 1 x 23 (a = 1, b = 3) 26

Cobb-Douglas Indifference Curves x 2 All curves are hyperbolic, asymptoting to, but never touching any axis. x 1 27

Marginal Utilities Marginal means “incremental”. n The marginal utility of commodity i is the rate-of-change of total utility as the quantity of commodity i consumed changes; i. e. n 28

Marginal Utilities n E. g. if U(x 1, x 2) = x 11/2 x 22 then 29

Marginal Utilities n E. g. if U(x 1, x 2) = x 11/2 x 22 then 30

Marginal Utilities n So, if U(x 1, x 2) = x 11/2 x 22 then 31

Marginal Utilities and Marginal Rates-of-Substitution n The general equation for an indifference curve is U(x 1, x 2) º k, a constant. Totally differentiating this identity gives 32

Marginal Utilities and Marginal Rates-of-Substitution rearranged is 33

Marginal Utilities and Marginal Rates-of-Substitution And rearranged is This is the MRS. 34

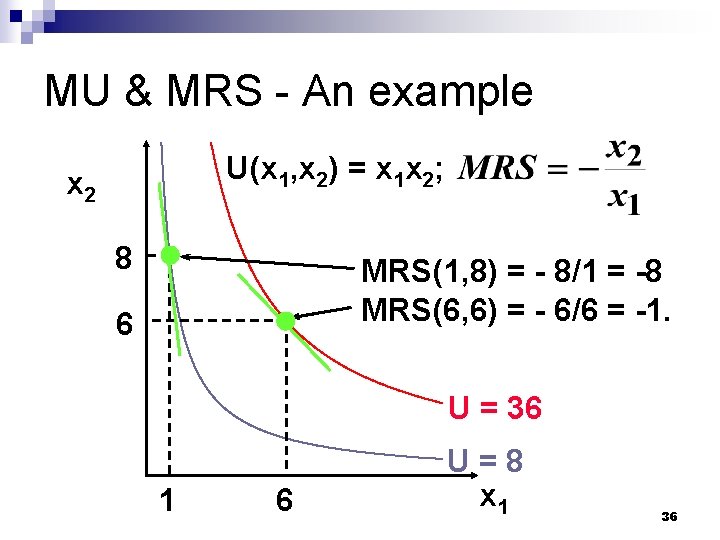
MU & MRS - An example n Suppose U(x 1, x 2) = x 1 x 2. Then so 35

MU & MRS - An example U(x 1, x 2) = x 1 x 2; x 2 8 MRS(1, 8) = - 8/1 = -8 MRS(6, 6) = - 6/6 = -1. 6 U = 36 1 6 U=8 x 1 36

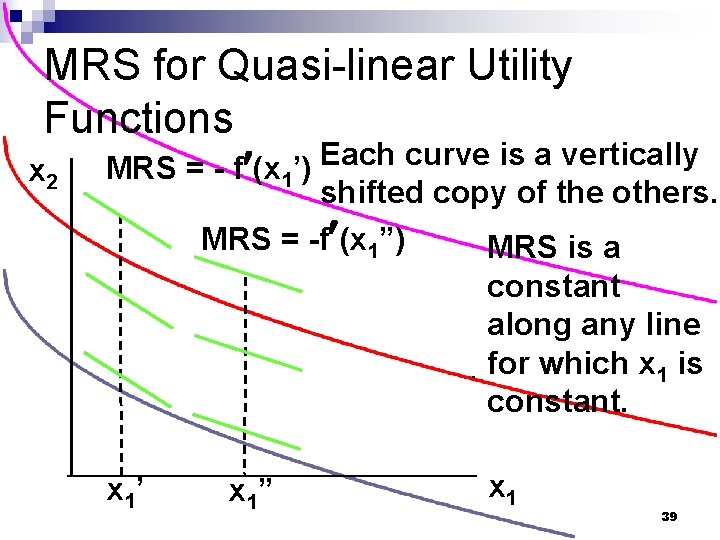
MRS for Quasi-linear Utility Functions n A quasi-linear utility function is of the form U(x 1, x 2) = f(x 1) + x 2. so 37

MRS for Quasi-linear Utility Functions n MRS = - f ¢ (x 1) does not depend upon x 2 so the slope of indifference curves for a quasi-linear utility function is constant along any line for which x 1 is constant. What does that make the indifference map for a quasi-linear utility function look like? 38

MRS for Quasi-linear Utility Functions Each curve is a vertically MRS = f (x ’) x 2 ¢ 1 shifted copy of the others. MRS = -f¢(x 1”) x 1’ x 1” MRS is a constant along any line for which x 1 is constant. x 1 39

Monotonic Transformations & Marginal Rates-of-Substitution Applying a monotonic transformation to a utility function representing a preference relation simply creates another utility function representing the same preference relation. n What happens to marginal rates-ofsubstitution when a monotonic transformation is applied? n 40

Monotonic Transformations & Marginal Rates-of-Substitution For U(x 1, x 2) = x 1 x 2 the MRS = - x 2/x 1. n Create V = U 2; i. e. V(x 1, x 2) = x 12 x 22. What is the MRS for V? n which is the same as the MRS for U. 41

Monotonic Transformations & Marginal Rates-of-Substitution n More generally, if V = f(U) where f is a strictly increasing function, then So MRS is unchanged by a positive monotonic transformation. 42